Skip to content

筑波大学 理工情報生命学術院 システム情報工学研究群 情報理工学位プログラム 2019年2月実施 基礎科目 問題 IV

Author

祭音Myyura

Description

\(N\) 個の頂点の集合 \(V\) と，\(M\) 本の辺の集合 \(E\) からなる無向グラフ \(G=(V,E)\) を考える． ここで，任意の頂点間における辺の数は高々１本であるとし，両端が同じ頂点となる辺は存在しないものとする．

この無向グラフ \(G\) は，隣接行列と呼ばれる \(N\) 次正方行列で表すことができる． この行列の \(i\) 行 \(j\) 列の要素を \(a_{i,j}\) とする． 頂点 \(v_i, v_j \in V \ (0 \le i \le N-1, 0 \le j \le N-1)\) の間に辺があるときは，\(a_{i,j} = a_{j,i} = 1\)，無いときは \(a_{i,j} = a_{j,i} = 0\) とする．

図 1 は，以下の隣接行列 \(A\) によって表される無向グラフにおいて，異なる頂点間の全ての経路を探すための C 言語のプログラムである． ここで，経路は，同じ頂点を度以上通ることがないものとする．

\[ A = \begin{bmatrix} 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix} \]

このとき，以下の問いに答えなさい．

(1) 隣接行列 \(A\) によって表される無向グラフを図で描きなさい．

(2) 関数 traverse は，引数 start で指定された頂点を始点とし，引数 goal で指定された頂点を終点とする全ての経路を標準出力に出力する． 配列 path には，探索途中の経路に現れる頂点の添字が始点から順に格納されている． また，配列 visited は，それぞれの頂点が始点から探索途中の頂点までの経路に現れているかを表している． 関数 traverse から呼び出される関数 dfs は，深さ優先探索により経路を探索する． 引数 step は，始点から現在探索している頂点までの経路上の辺の数を表している． 図の空欄 (a)～(e)を埋めてプログラムを完成させなさい．

(3) 図 1 のプログラムを実行したときに，標準出力に出力される結果を答えなさい．

(4) 図 1 のプログラムを実行したときに，関数 dfs が呼び出される回数を答えなさい．

(5) 疎な無向グラフ（辺の数が少ない無向グラフ）を対象とする場合，図のプログラムを修正することにより，時間計算量を削減することができる． その修正の概要を説明しなさい．また，修正によって時間計算量が削減される理由を説明しなさい．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <stdbool.h>
#define N 7

const int a[N][N] = {
    {0, 1, 1, 0, 0, 0, 0},
    {1, 0, 1, 1, 0, 0, 0},
    {1, 1, 0, 0, 1, 0, 0},
    {0, 1, 0, 0, 1, 1, 0},
    {0, 0, 1, 1, 0, 0, 1},
    {0, 0, 0, 1, 0, 0, 0},
    {0, 0, 0, 0, 1, 0, 0},
};

void print_path(int n, int path[])
{
    for (int i = 0; i < n; i++)
        printf("%d ", path[i]);
    printf("\n");
}

void dfs(int step, int goal, int path[], bool visited[])
{
    int x = path[step- 1];
    if (x == goal) {
        print_path(step, path);
    } else {
        for (int i = 0; i < N; i++) {
            if (a[x][i] == 0) continue;
            if (!visited[i]) {
                path[[空欄 (a)]] = i;
                visited[i] = [空欄 (b)];
                dfs([空欄 (c)], [空欄 (d)], path, visited);
                visited[i] = [空欄 (e)];
            }
        }
    }
}

void traverse(int start, int goal)
{
    int path[N];
    bool visited[N];

    for (int i = 0; i < N; i++) visited[i] = false;
    path[0] = start;
    visited[start] = true;
    dfs(1, goal, path, visited);
}

int main(void)
{
    traverse(0, 6);
    return 0;
}

Kai

(1)

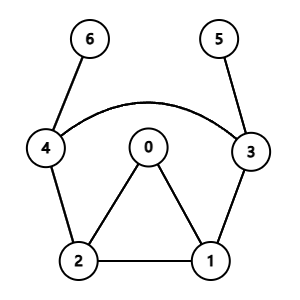
(2)

  • [空欄 (a)]: step
  • [空欄 (b)]: 1
  • [空欄 (\(c\))]: step + 1
  • [空欄 (d)]: goal
  • [空欄 (e)]: 0

(3)

1
2
3
4
0 1 2 4 6 
0 1 3 4 6 
0 2 1 3 4 6 
0 2 4 6

(4)

関数 dfs が呼び出される回数は 23 回である。

(5)

隣接行列の代わりに、隣接リストを使ってグラフを表す。

隣接行列を使用した場合、ある頂点から隣接する頂点を見つけるために、その頂点の行を全て調べる必要があるため、DFS の時間計算量は \(O(|V|^2)\) である。

隣接リストを使用した場合、すべての頂点を1回ずつ訪れ、その頂点の隣接する頂点を調べる必要があるため、DFS の時間計算量は \(O(|V| + |E|)\) である。

よって、疎なグラフ（辺の数 \(|E|\) が \(|V|^2\) よりもずっと少ない）の場合、隣接リストを使用した DFS の方が効率的である。