筑波大学理工情報生命学術院システム情報工学研究群情報理工学位プログラム 2018年2月実施基礎科目問題 IV

Author

祭音Myyura

Description

小さい順 (昇順，ascending order) に並んだ整数を保持するリストを，C 言語の配列で実装する. 図 1 に，そのための構造体 ilist を示す. メンバ array は，配列の先頭，メンバ size は，リストの要素数，メンバ capacity は，配列の容量を保持する. 図 2 に，構造体 ilist の例を示す. 構造体 ilist は，表 1 に示した関数で操作される.

struct ilist {
    int *array;
    int  size;
    int  capacity;
};

図 1: 整数のリストを保持する構造体 ilist の定義.

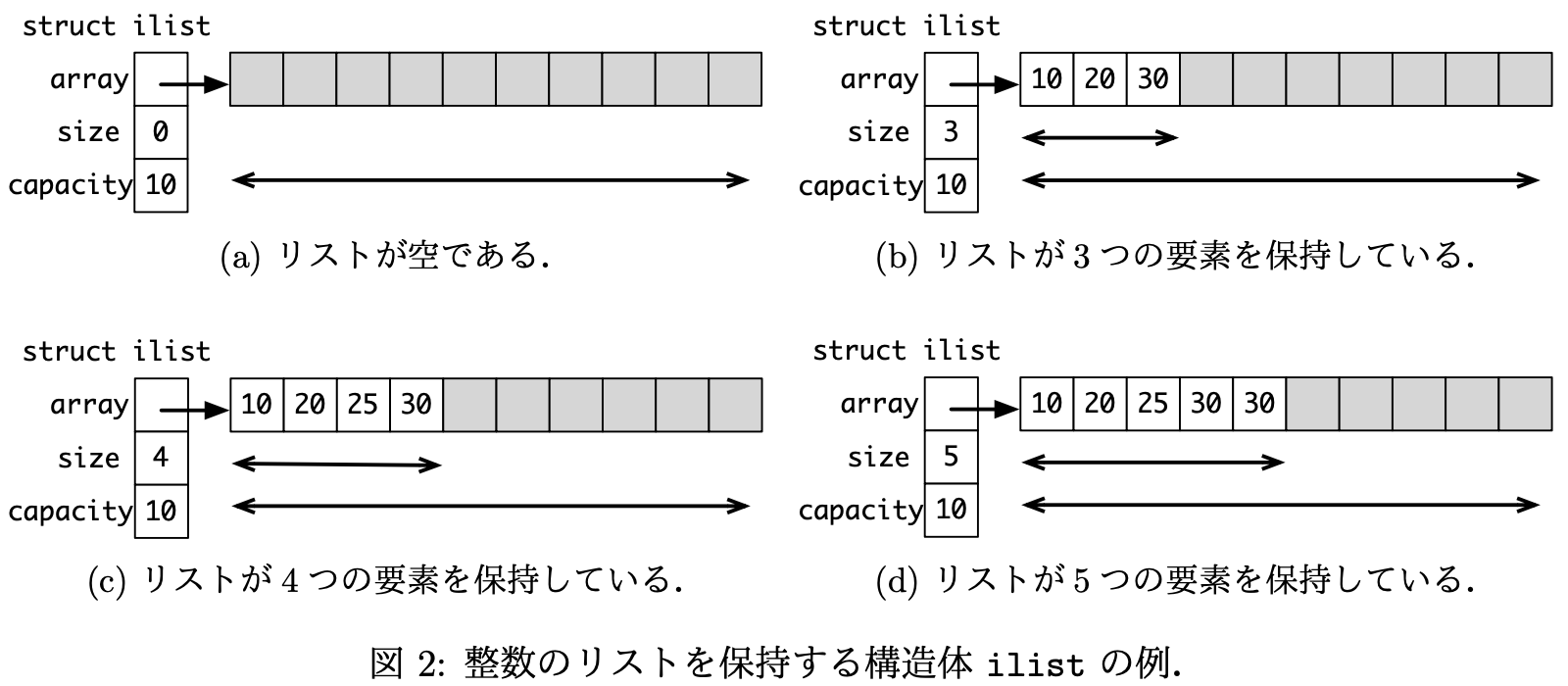
表 1: 構造体 ilist を操作する関数.

関数	説明
struct ilist *new_ilist()	構造体と配列のためにメモリを割り当て，構造体のメンバを初期化し，構造体へのポインタを返す.
void free_ilist(struct ilist *l)	構造体，および，その配列のメモリを解放する.
void expand(struct ilist *l)	構造体の配列を拡張し，容量を増やす.
void insert(struct ilist *l, int x)	構造体の，要素が小さい順に並んだ配列に整数を挿入する. 挿入後も配列は小さい順に並んでいる.
void append(struct ilist *l, int x)	構造体の配列の末尾に整数を追加する. この関数は配列の容量が不足していた場合，関数 expand() を呼び容量を増やす.

次の問いに答えなさい.

(1) 次の関数 make_list() は，空のリストを割り当て，そのリストに3つの整数を加え，図 2(b) のようなリストを返す.表 1 に示した関数を用いて空欄を埋めて，関数を完成させなさい.

struct ilist *make_list() {
    struct ilist *l = new_ilist();
    [ 空欄 (A) ] (l, [ 空欄 (B) ]);
    [ 空欄 (C) ] (l, 10);
    append (l, [ 空欄 (D) ]);
    return (l);
}

(2) 次の関数 uniq() は，引数として与えられたリストを読み，連続して現れる要素を比較し，重複を排除したリスト (ユニークな要素を含むリスト) を返す. たとえば，この関数は，図 2(d) のようなリストを取ると，図 2© のようなリストを返す. 空欄を埋めて，関数を完成させなさい.

struct ilist *uniq(struct ilist *l) {
    struct ilist *u;
    int x, i;
    u = new_ilist();
    if ([ 空欄 (E) ])
        return (u);
    x = [ 空欄 (F) ];
    append(u, x);
    for ([ 空欄 (G) ]) {
        if ([ 空欄 (H) ]) {
            x = [ 空欄 (I) ];
            append(u, x);
        }
    }
    return (u);
}

(3) 次の関数 merge() は，2つのリストを引数として取り，それらを1つのリストへマージする. ただしこの関数は，引数の各リストが小さい順に並んでいることを前提としている.空欄を埋めて，関数を完成させなさい.

struct ilist *merge(struct ilist *a, struct ilist *b) {
    struct ilist *l;
    int i, j;
    l = new_ilist();
    i = 0; j = 0;
    while ([ 空欄 (J) ]) {
        if ([ 空欄 (K) ]) {
            append(l, [ 空欄 (L) ]);
            i++;
        }
        else {
            append(l, [ 空欄 (M) ]);
            j++;
        }
    }

    if ([ 空欄 (N) ]) {
        for (; i < a->size; i++) {
            append(l, [ 空欄 (O) ]);
        }
    }
    else {
        for (; j < b->size; j++) {
            append(l, [ 空欄 (P) ]);
        }
    }
    return (l);
}

(4) 次の関数 insert() は，関数 expand() と find_pos() を利用し，整数 x をリスト l に挿入する. 関数 insert() は，そのリストが小さい順に並んでいることを前提としている. 関数 expand() は必ず成功するものとする. 関数 find_pos() は，二分探索法を用いている. 空欄を埋めて，関数を完成させなさい.

void insert(struct ilist *l, int x) {
    int i, j;
    if (l->size == l->capacity)
        expand(l);
    i = find_pos(l, x);
    for ([ 空欄 (Q) ]) {
        l->array[j+1] = l->array[j];
    }
    l->array[i] = x;
    l->size++;
}

void expand(struct ilist *l) {
    // コード省略
}

int find_pos(struct ilist *l, int x) {
    int lower, upper, i;
    lower = 0;
    upper = l->size;
    while ([ 空欄 (R) ]) {
        i = [ 空欄 (S) ];
        if (x == l->array[i]) {
            return [ 空欄 (T) ];
        }
        else if ([ 空欄 (U) ]) {
            upper = i;
        }
        else {
            [ 空欄 (V) ];
        }
    }
    return (lower);
}

(5) 設問 (4) の関数 find_pos() の計算の複雑さをオーダー記法 \(O()\) で表記しなさい.ただし，リストの要素数を \(n\) とする.

(6) 設問 (4) の関数 insert() には，その実行時間がリストの要素数が増えるに従い増大するという問題がある. リストの要素数を \(n\) とする. 関数 expand() の計算の複雑さが \(O(1)\) である時，関数 insert() の計算の複雑さをオーダー記法 \(O()\) で表記しなさい.

(7) 関数 expand() の計算の複雑さが \(O(1)\) である時，設問 (4) の関数 insert() とは異なり，関数 append() の実行時間は，リストの要素数が増えても増大しない. その理由を説明しなさい.

(8) 設問 (6) の問題が深刻な場合，データ構造として配列を使うべきではない. 配列の代替となるより良いデータ構造を示しなさい. その代替データ構造が元のものより良い理由を説明しなさい.

Kai

(1)

[ 空欄 (A) ]: append
[ 空欄 (B) ]: 20
[ 空欄 (C) ]: insert
[ 空欄 (D) ]: 30

struct ilist *make_list() {
    struct ilist *l = new_ilist();
    append (l, 20);
    insert (l, 10);
    append (l, 30);
    return (l);
}

(2)

[ 空欄 (E) ]: l->size == 0
[ 空欄 (F) ]: l->array[0]
[ 空欄 (G) ]: i = 1; i < l->size; i++
[ 空欄 (H) ]: x != l->array[i]
[ 空欄 (I) ]: l->array[i]

struct ilist *uniq(struct ilist *l) {
    struct ilist *u;
    int x, i;
    u = new_ilist();
    if (l->size == 0)
        return (u);
    x = l->array[0];
    append(u, x);
    for (i = 1; i < l->size; i++) {
        if (x != l->array[i]) {
            x = l->array[i];
            append(u, x);
        }
    }
    return (u);
}

(3)

[ 空欄 (J) ]: i < a->size && j < b->size
[ 空欄 (K) ]: a->array[i] < b->array[j]
[ 空欄 (L) ]: a->array[i]
[ 空欄 (M) ]: b->array[j]
[ 空欄 (N) ]: i < a->size
[ 空欄 (O) ]: a->array[i]
[ 空欄 (P) ]: b->array[j]

struct ilist *merge(struct ilist *a, struct ilist *b) {
    struct ilist *l;
    int i, j;
    l = new_ilist();
    i = 0; j = 0;
    while (i < a->size && j < b->size) {
        if (a->array[i] < b->array[j]) {
            append(l, a->array[i]);
            i++;
        }
        else {
            append(l, b->array[j]);
            j++;
        }
    }

    if (i < a->size) {
        for (; i < a->size; i++) {
            append(l, a->array[i]);
        }
    }
    else {
        for (; j < b->size; j++) {
            append(l, b->array[j]);
        }
    }
    return (l);
}

(4)

[ 空欄 (Q) ]: j = l->size - 1; j >= i; j--
[ 空欄 (R) ]: lower < upper
[ 空欄 (S) ]: (lower + upper) / 2
[ 空欄 (T) ]: i
[ 空欄 (U) ]: x < l->array[i]
[ 空欄 (V) ]: lower = i + 1

void insert(struct ilist *l, int x) {
    int i, j;
    if (l->size == l->capacity)
        expand(l);
    i = find_pos(l, x);
    for (j = l->size-1; j >= i; j--) {
        l->array[j+1] = l->array[j];
    }
    l->array[i] = x;
    l->size++;
}

int find_pos(struct ilist *l, int x) {
    int lower, upper, i;
    lower = 0;
    upper = l->size;
    while (lower < upper) {
        i = (lower + upper) / 2;
        if (x == l->array[i]) {
            return i;
        }
        else if (x < l->array[i]) {
            upper = i;
        }
        else {
            lower = i + 1;
        }
    }
    return (lower);
}

(5)

\(O(\log n)\)

(6)

\(O(n)\)

(7)

関数 append() は、下記の通り実装すれば、その計算量はリストの要素数に無関係で、\(O(1)\) である。

void append(struct ilist *l, int x) {
    if (l->size == l->capacity)
        expand(l);
    l->array[l->size++] = x;
}

(8)

連結リスト（Linked List）を使うこと。

筑波大学 理工情報生命学術院 システム情報工学研究群 情報理工学位プログラム 2018年2月実施 基礎科目 問題 IV