Skip to content

筑波大学 理工情報生命学術院 システム情報工学研究群 情報理工学位プログラム 2017年8月実施 基礎科目 情報2

Author

祭音Myyura

Description

情報2 (1)

以下の関数により正の整数の追加と取り出しができる一種の優先度キュー (priority queue) を C 言語で構造体 pq として実装することを考える．

  • struct pq *newq(), 新たに優先度キューを作成して初期化し，そのキューへのポインタを返す．
  • void putq(struct pq *q, int v), 正の整数 v を優先度キュー q に追加する．
  • int getq(struct pq *q), 優先度キュー q に格納されている整数のうち最も値が大きいものを一つキューから取り出し，その値を返す．ただし，キューが空の場合には，この関数は −1 を返す．

ここではこの優先度キューを，以下のような完全 2 分木のデータ構造を用いて実現する．

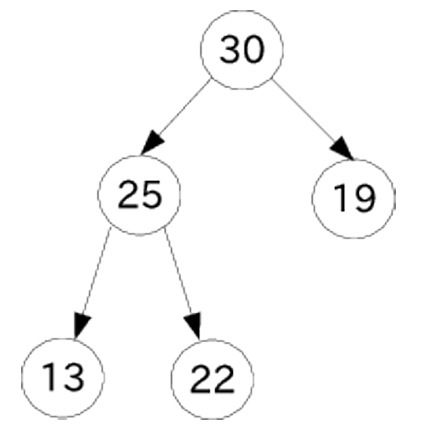
上図の各ノードの中に書かれている数値が，優先度キューに格納される数値である． この完全 2 分木には，以下のような条件を満足するように数値が格納されている．

  • 各ノードが持つ数値は，そのノードのいずれの子ノードが持つ数値より小さくない．

(a). 上記の条件で \(n\) 個の正の整数が格納された完全 2 分木を考える． この \(n\) 個の正の整数を，その根から幅優先で走査した順に配列の要素 a[1] ～ a[n] に格納したとする． 例えば，上図の完全 2 分木であれば，数値は 30, 25, 19, 13, 22 の順に配列の要素 a[1] ～ a[5]に格納される． 以下の空欄 [ (A) ] ～ [ (C) ] を埋めて文章を完成させなさい．

  • 整数 \(i\ (1 \le i \le \frac{n}{2})\) に対して，a[i] の子ノードの数値は [ (A) ] と [ (B) ] に格納される．
  • 配列 a[1] ～ a[n] で最も大きな数値は [ (C) ] に格納される．

(b). 以下のプログラムは上記の (a) に示した配列 a を用いて構造体 pq と関数 newq，putq，getq を実装したものである． ただし、a[0] には定数 INT_MAX の値を代入している． この定数 INT_MAX の値は優先度キューに追加されるどの整数よりも大きな値であるものとする． また，以下のプログラムで定数 SIZE の値は十分に大きく，優先度キューに格納される整数の個数がこの値を超えることはないものとする．

空欄 [ (D) ] ~ [ (F) ] を埋めてこれらの関数を完成させなさい．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
struct pq {
    int n;
    int a[SIZE];
};

struct pq *newq()
{
    struct pq *q = malloc(sizeof(struct pq));
    q->n = 0;
    q->a[0] = INT_MAX;
    return q;
}

void putq(struct pq *q, int v)
{
    int i = ++(q->n);
    while (q->a[i/2] <= v) {
        q->a[i] = q->a[[ 空欄 (D) ]];
        i = i / 2;
    }
    q->a[i] = v;
}

int getq(struct pq *q)
{
    int i = 1, j, v, w;
    if (q->n == 0) {
        return [ 空欄 (E) ];
    }
    v = q->a[1];
    w = q->a[(q->n)--];
    while (i <= (q->n) / 2) {
        j = 2 * i;

        if (j < q->n && q->a[j] < q->a[j+1]) j++;

        if (w >= q->a[j]) {
            break;
        } else {
            [ 空欄 (F) ];
            i = j;
        }
    }
    q->a[i] = w;
    return v;
}

(\(c\)). n 個の整数が格納されている優先度キュー q を引数として関数 getq を呼び出したときの最悪の場合の漸近的な時間計算量を以下から選びなさい．

  • (i) 時間計算量は \(O(1)\) である．
  • (ii) 時間計算量は \(O(\log n)\) であり，\(O(1)\) ではない．
  • (iii) 時間計算量は \(O(n)\) であり，\(O(\log n)\) ではない．
  • (iv) 時間計算量は \(O(n \log n)\) であり，\(O(n)\) ではない．
  • (v) 時間計算量は \(O(n^2)\) であり，\(O(n \log n)\) ではない．

(d). プログラムの 10 行目では，q->a[0] に INT_MAX が代入されている．もし INT_MAX の代わりに q->a[0] に 0 が代入されたとするとどのような問題が生じるか，説明しなさい．

情報2 (2)

次ページに掲載されている C 言語で記述されたプログラムリストについての以下の設問に答えなさい．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#define UNREACH -1
#define N_VERT 8
const int adj_mat[N_VERT][N_VERT] = {
    {0, 1, 0, 1, 0, 1, 0, 0},
    {0, 0, 1, 0, 0, 0, 0, 0},
    {0, 0, 0, 1, 0, 0, 0, 0},
    {0, 0, 0, 0, 1, 0, 0, 0},
    {0, 0, 0, 0, 0, 1, 0, 1},
    {0, 0, 0, 0, 0, 0, 1, 0},
    {0, 0, 1, 0, 0, 0, 0, 1},
    {1, 0, 0, 0, 0, 0, 0, 0},
};

void calc_dists(const int origin, int dist_vec[]) {
    int adj_list[N_VERT * N_VERT], adj_index[N_VERT + 1];
    int array1[N_VERT], array2[N_VERT];
    int *curr = array1, *next = array2, *tmp;
    int i, j, index = 0, dist = 1, len_curr = 1, len_next = 0;

    for (i = 0; i < N_VERT; i++) {
        adj_index[i] = index;
        for (j = 0; j < N_VERT; j++) {
            if (adj_mat[i][j] == 1) {
                adj_list[index++] = j;
            }
        }
    }
    adj_index[N_VERT] = index;

    for (i = 0; i < N_VERT; i++) {
        dist_vec[i] = UNREACH;
    }

    curr[0] = origin;
    dist_vec[origin] = 0;
    while (len_curr > 0) {
        for (i = 0; i < len_curr; i++) {
            for (j = [ 空欄 (G) ]; j < [ 空欄 (H) ]; j++) {
                if ([ 空欄 (I) ] ==  [ 空欄 (J) ]) {
                    [ 空欄 (K) ] = dist;
                    [ 空欄 (L) ] = [ 空欄 (M) ];
                    len_next++;
                }
            }
        }
        tmp = next;
        next = curr;
        curr = tmp;
        len_curr = len_next;
        len_next = 0;
        dist++;
    }
}

(a). プログラムリストの 3 行目から 12 行目にある 2 次元配列 adj_mat は，頂点 \(0, 1, \ldots, 7\) の 8 つの頂点を持つ重みなし有向グラフを示す隣接行列である． グラフの頂点番号は配列の添え字に対応し，adj_mat[i][j] が 1 のとき，頂点 i から頂点 j への辺が存在することを表している． 下図は，この adj_mat で表現されているグラフを図示したものである． (A) から (F) までに入る適切な整数を答えよ．

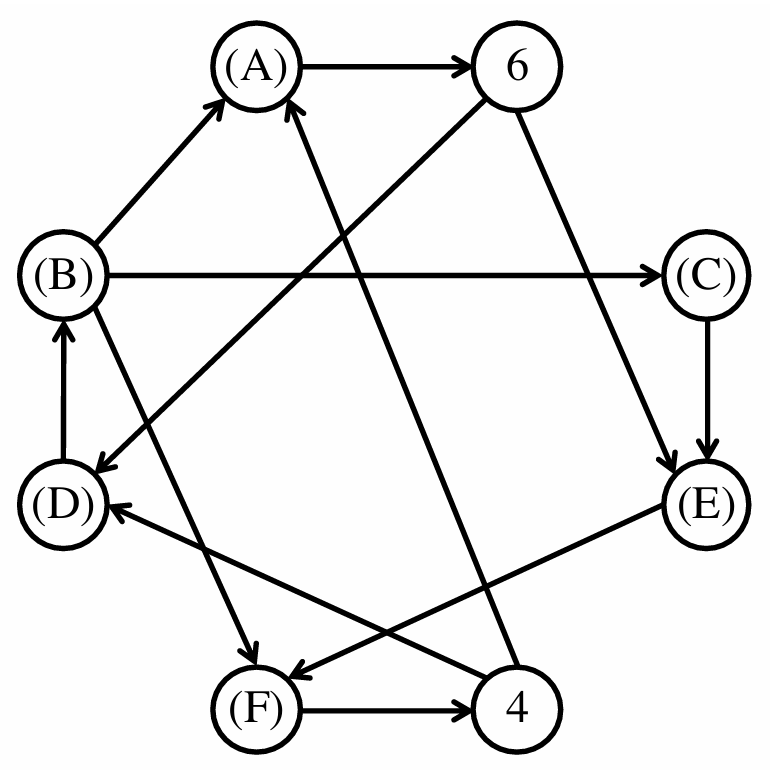
(b). プログラムリストの 14 行目から定義されている関数 calc_dists は，adj_mat で定義されたグラフの指定された頂点 (origin) から，グラフ上のすべての頂点への距離を計算する． ここで，頂点 i から頂点jまでの距離とは，i から j へ到達するために通らなくてはならない辺の数の最小値である． (a) のグラフにおいて，origin を \(0\) としたときの，頂点 \(0, 1, ..., 7\) への距離を示せ．

(\(c\)). プログラムリストの 20 行目から 28 行目では，adj_mat を隣接リストの形に変換している． この処理を実行させた後に配列 adj_list および adj_index に代入されている値を書け． 但し，値が初期化されていない要素は書かないこと．

(d). プログラムリスト 30 行目から 52 行目では，配列 adj_list および adj_index を用いて，origin から頂点i \((\text{i}=0, 1, ..., 7)\) までの距離を origin からの幅優先探索で求め，dist_vec[i] に格納している． 但し，origin から頂点 i に到達できない場合は，dist_vec[i] の値は UNREACH とする． (G) から (M) に入るべき式を入れて，プログラムを完成させよ．

Kai

情報2 (1)

(a)

  • [ (A) ]: 2i
  • [ (B) ]: 2i + 1
  • [ (C) ]: a[1]

(b)

  • [ (D) ]: i / 2
  • [ (E) ]: -1
  • [ (F) ]: q->a[i] = q->a[j]

(\(c\))

(ii)

(d)

i=0 のとき、i/2 も 0 になるから、 putq の while 文の条件

  • q->a[i/2] = q->a[0] = 0 <= v

は常に満たされていて、無限ループになる。

情報2 (2)

(a)

  • (A): 5
  • (B): 0
  • (C): 1
  • (D): 7
  • (E): 2
  • (F): 3

(b)

  • dist(0, 0): 0
  • dist(0, 1): 1
  • dist(0, 2): 2
  • dist(0, 3): 1
  • dist(0, 4): 2
  • dist(0, 5): 1
  • dist(0, 6): 2
  • dist(0, 7): 3

(\(c\))

1
2
3
adj_index: 0, 3, 4, 5, 6, 8, 9, 11

adj_list: 1, 3, 5, 2, 3, 4, 5, 7, 6, 2, 7, 0

(d)

  • [ (G) ]: adj_index[curr[i]]
  • [ (H) ]: adj_index[curr[i] + 1]
  • [ (I) ]: dist_vec[adj_list[j]]
  • [ (J) ]: UNREACH
  • [ (K) ]: dist_vec[adj_list[j]]
  • [ (L) ]: next[len_next]
  • [ (M) ]: adj_list[j]