東京大学 数理科学研究科 数理科学専攻 2021年度 専門科目 B 第16問

Author

Miyake

Description

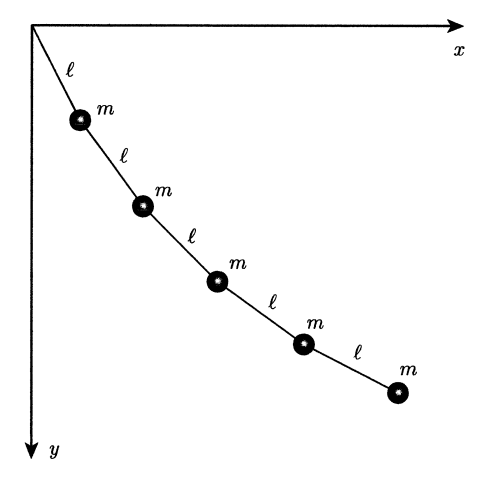
質量が \(m\) のおもりを \(N\) 個用意し、図のように長さが \(l\) の \(N\) 本のひもで順につないで天井からぶら下げる。 ひもはたわんだり伸び縮みしたりせず、ひもの重さは無視でき、おもりの運動は鉛直軸を含む一定の平面内で起こるものとする。 また、時刻を \(t\)、重力加速度を \(g\) で表すことにする。 図のように、運動が行われる平面の \(xy\) 座標を、天井とひもとの固定点を原点とし、水平方向が \(x\)、鉛直下向きを \(y\) となるように定める。 上から数えて \(i\) 番目のおもりの水平方向の位置座標を \(x_i\) とする。

(1) どの \(|x_i|\) も十分小さいという仮定のもとで、この系のLagrangian \(L\)、および \(L\) から得られる Euler-Lagrange 方程式を求めよ。 ただし、こうして得られる Euler-Lagrange 方程式は、線型の微分方程式になるものとする。

(2) (1)で求めた線型微分方程式の解で、定数 \(\omega\) を用いて

\[ x_i = A_i \sin{\omega t} \ \ \ \ \ (i = 1, 2, \cdots, N) \]

と表される解に興味があるとする。 このとき、最高次の係数が \(1\) のある整数係数 \(N\) 次多項式 \(P_N (X)\) が存在し、上の形の解が存在するための必要十分条件が、\(P_N(\omega^2 \frac{l}{g})=0\) と表されることを示せ。

(3) 多項式列 \(\{P_N(X) \mid N = 1, 2, 3, \cdots\}\) を特徴付ける漸化式を一つ求めよ。

Kai

(1)

位置座標 \(x\) の時間微分 \(dx/dt, d^2x/dt^2\) を それぞれ \(\dot{x}, \ddot{x}\) のように表す。

どの \(|x_i|\) も十分に小さく、 得られる Euler-Lagrange 方程式が線型の微分方程式とのことなので、 運動エネルギーとポテンシャルエネルギーは \(\{x_i\}\) に関して2次まで求めればよい。

上から数えて \(i\) 番目のおもりのy座標を \(y_i\) とすると、 次が成り立つ：

\[ \begin{aligned} x_1^2 + y_1^2 &= l^2 , \\ (x_n - x_{n-1})^2 + (y_n - y_{n-1})^2 &= l^2 \ \ \ \ (n = 2, 3, \cdots, N) \end{aligned} \]

よって、

\[ \begin{aligned} y_1 &\simeq l - \frac{x_1^2}{2l} , \\ y_n &\simeq nl - \frac{1}{2l} \left( x_1^2 + \sum_{j=1}^{n-1} (x_j - x_{j+1})^2 \right) \ \ \ \ (n = 2, 3, \cdots, N) \end{aligned} \]

なので、この系のポテンシャルエネルギーは（基準点を適当に選んで）

\[ \begin{aligned} U &= - mg \sum_{i=1}^N y_i \\ &\simeq - mg \left[ \frac{1}{2}N(N+1) l - \frac{1}{2l} \left( N x_1^2 + \sum_{j=1}^{N-1} (N-j) (x_j - x_{j+1})^2 \right) \right] \end{aligned} \]

であり、

\[ \begin{aligned} \frac{\partial U}{\partial x_1} &\simeq \frac{mg}{l} \left[ (2N-1) x_1 - (N-1) x_2 \right] , \\ \frac{\partial U}{\partial x_n} &\simeq \frac{mg}{l} \left[ -(N-n+1) x_{n-1} + (2N-2n+1) x_n - (N-n) x_{n+1} \right] & \ \ \ \ (n = 2, 3, \cdots, N-1) , \\ \frac{\partial U}{\partial x_N} &\simeq \frac{mg}{l} \left[ - x_{N-1} + x_N \right] \end{aligned} \]

である。

また、 \(\dot{x}_i\) にくらべて \(\dot{y}_i\) は十分小さいので、 この系の運動エネルギーは

\[ \begin{aligned} T &= \frac{1}{2} m \sum_{i=1}^N \left( \dot{x}_i^2 + \dot{y}_i^2 \right) \\ &\simeq \frac{1}{2} m \sum_{i=1}^N \dot{x}_i^2 \end{aligned} \]

であり、

\[ \begin{aligned} \frac{\partial T}{\partial \dot{x}_n} &\simeq m \dot{x}_n & \ \ (n = 1, 2, \cdots, N) \end{aligned} \]

である。

よって、Langrangian \(L\) は、

\[ \begin{aligned} L &= T - U \\ &\simeq \frac{1}{2} m \sum_{i=1}^N \dot{x}_i^2 + mg \left[ \frac{1}{2}N(N+1) l - \frac{1}{2l} \left( N x_1^2 + \sum_{j=1}^{N-1} (N-j) (x_j - x_{j+1})^2 \right) \right] \end{aligned} \]

であり、Euler-Lagrange 方程式は、

\[ \begin{aligned} \ddot{x}_1 &= - \frac{g}{l} \left[ (2N-1) x_1 - (N-1) x_2 \right] , \\ \ddot{x}_n &= - \frac{g}{l} \left[ -(N-n+1) x_{n-1} + (2N-2n+1) x_n - (N-n) x_{n+1} \right] & \ \ \ \ (n = 2, 3, \cdots, N-1) , \\ \ddot{x}_N &= - \frac{g}{l} \left[ - x_{N-1} + x_N \right] \end{aligned} \]

である。

(2)

(1) で得た運動方程式に \(x_i = A_i \sin \omega t \ \ (i = 1, 2, \cdots N)\) を代入して整理すると、次のようになる：

\[ \begin{align} \left( \omega^2 \frac{l}{g} I_N - B_N \right) \begin{pmatrix} A_1 \\ A_2 \\ \vdots \\ A_N \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \tag{a} \label{a} \end{align} \]

ただし、 \(I_N\) は \(N\) 次の単位行列で、 \(B_N\) は \(i,j\) 成分が次のように与えられる \(N\) 次正方行列である：

\[ \begin{aligned} (B_N)_{i,j} &= \begin{cases} 2N-2i+1, &(i-j=0) \\ -N+i, &(i-j=-1)\\ -N+i-1, &(i-j=1)\\ 0, &(\text{otherwise}) \end{cases} \end{aligned} \]

(\(\ref{a}\)) が自明な解 \(A_1 = A_2 = \cdots = A_N = 0\) 以外の解 \(A_1, A_2, \cdots, A_N\) をもつための必要十分条件は

\[ \begin{aligned} \det \left( \omega^2 \frac{l}{g} I_N - B_N \right) = 0 \end{aligned} \]

であるが、これの左辺は \(\omega^2 l/g\) に関して 最高次の係数が \(1\) の整数係数の \(N\) 次の多項式である。 よって、

\[ \begin{aligned} P_N(X) = \det \left( X I_N - B_N \right) \end{aligned} \]

として、題意を満たすことがわかる。

(3)

\(N = 1, 2, \cdots\) について、

\[ \begin{aligned} P_{N+2} (X) &= \det \begin{pmatrix} X-(2N+3) & N+1 & 0 & 0 & 0 & 0 & \cdots \\ N+1 & X-(2N+1) & N & 0 & 0 & 0 & \cdots \\ 0 & N & X-(2N-1) & N-1 & 0 & 0 & \cdots \\ 0 & 0 & N-1 & X-(2N-3) & N-2 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{pmatrix} \\ &= (X-(2N+3)) \det \begin{pmatrix} X-(2N+1) & N & 0 & 0 & 0 & \cdots \\ N & X-(2N-1) & N-1 & 0 & 0 & \cdots \\ 0 & N-1 & X-(2N-3) & N-2 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{pmatrix} \\ & \ \ \ \ - (N+1) \det \begin{pmatrix} N+1 & 0 & 0 & 0 & 0 & \cdots \\ N & X-(2N-1) & N-1 & 0 & 0 & \cdots \\ 0 & N-1 & X-(2N-3) & N-2 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{pmatrix} \\ &= (X-(2N+3)) \det \begin{pmatrix} X-(2N+1) & N & 0 & 0 & 0 & \cdots \\ N & X-(2N-1) & N-1 & 0 & 0 & \cdots \\ 0 & N-1 & X-(2N-3) & N-2 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{pmatrix} \\ & \ \ \ \ - (N+1)^2 \det \begin{pmatrix} X-(2N-1) & N-1 & 0 & 0 & \cdots \\ N-1 & X-(2N-3) & N-2 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{pmatrix} \\ &= (X-(2N+3)) P_{N+1}(X) - (N+1)^2 P_N(X) \end{aligned} \]

が成り立つ。