東京大学 新領域創成科学研究科 海洋技術環境学専攻 2022年度
Author
Miyake
Description
第1問
以下の定積分の値を求めよ。
\[
\int_0^{\pi} e^x \sin(x) \cos(x) dx
\]
第2問
\(\text{O} - xyz\)座標系上に点\(A\)、\(B\)、\(C\)がそれぞれ\((4, 5, 7)\)、\((2, 1, 3)\)、\((9, 7, 6)\)で与えられる時、以下を求めよ。
(1) 三角形 \(OAB\) の面積。
(2) 四面体 \(OABC\) の体積。
第3問
観測点 \(O\) から \(200\) メートル離れた同じ水平面上にある地点 \(P\) から、鉛直に毎分 \(25\) メートルの速度で風船を上げる。
風船の位置を \(B\) とし、観測点から風船を見上げた角度を \(\angle BOP\) とする。
風船が地点 \(P\) から \(100\) メートルの高さに達したとき、\(\angle BOP\) の時間変化率を求めよ。ただし、風船の大きさは考えない。
第4問
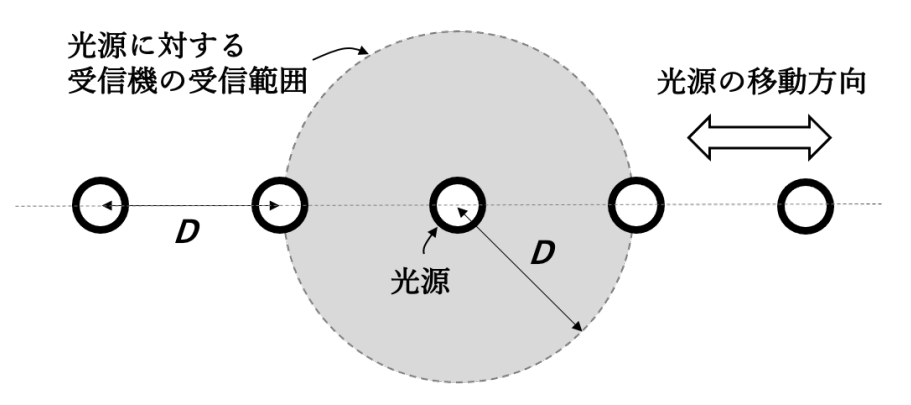
図のように直線上を無数の光源が一定の間隔 \(D\) を保って移動している。光は光源から放
射状に広がり、受信機は光源から \(D\) の距離まで光を受信できるものとする。受信機は光
源が並ぶ直線から距離 \(L\) だけ離れた平行な直線の上に一定の間隔 \(D/2\) で固定されてい
る。光源と受信機の大きさは無視する。
(1) \(1\) つの光源からの光を常に \(1\) つ以上の受信機で受信できる \(L\) の最大値を求めよ。
(2) \(1\) つの光源からの光を常に \(2\) つ以上の受信機で受信できる \(L\) の最大値を求めよ。
Kai
第1問
\[
\begin{aligned}
I
&= \int_0^\pi e^x \sin(x) \cos(x) dx
\\
&= \frac{1}{2} \int_0^\pi e^x \sin(2x) dx
\\
&= \frac{1}{2} \left[ e^x \sin(2x) \right]_0^\pi - \int_0^\pi e^x \cos(2x) dx
\\
&= - \left[ e^x \cos(2x) \right]_0^\pi - 2 \int_0^\pi e^x \sin(2x) dx
\\
&= - e^\pi + 1 - 4I
\\
\therefore \ \
5 I &= 1 - e^\pi
\\
\therefore \ \
I &= \frac{1 - e^\pi}{5}
\end{aligned}
\]
第2問
(1)
\[
\begin{aligned}
\frac{1}{2}
\left|
\overrightarrow{\mathrm{OA}} \times \overrightarrow{\mathrm{OB}}
\right|
&= \frac{1}{2} \left| (8, 2, -6) \right|
\\
&= \frac{1}{2} \cdot 2 \sqrt{26}
\\
&= \sqrt{26}
\end{aligned}
\]
(2)
\[
\begin{aligned}
\frac{1}{6}
\left|
\left( \overrightarrow{\mathrm{OA}} \times \overrightarrow{\mathrm{OB}} \right)
\cdot \overrightarrow{\mathrm{OC}}
\right|
&= \frac{1}{6} \cdot 50
\\
&= \frac{25}{3}
\end{aligned}
\]
第3問
\(\theta = \angle \mathrm{BOP}\) (ラジアン) とし、
\(\mathrm{B}\) の \(\mathrm{P}\) からの高さを \(h\) (メートル) とする。
また、それぞれの時間変化率 (毎分) を \(\dot{\theta}, \dot{h} = 25\) とする。
このとき、
\[
\begin{aligned}
\tan \theta = \frac{h}{200}
\end{aligned}
\]
であり、
\[
\begin{aligned}
\frac{\dot{\theta}}{\cos^2 \theta} = \frac{\dot{h}}{200}
\end{aligned}
\]
が成り立つ。
よって、 \(h=100\) のとき \(\tan \theta = 1/2\) したがって
\(\cos^2 \theta = 4/5\) であるので、このとき、
\[
\begin{aligned}
\dot{\theta}
&= \frac{4}{5} \cdot \frac{25}{200}
\\
&= \frac{1}{10}
\end{aligned}
\]
である。
第4問
(1)
1つの光源を中心とする半径 \(D\) の円を考える。
1つの受信機がこの円から出る瞬間に、その隣の受信機がこの円に入るとすると、
\[
\begin{aligned}
L^2
&= D^2 - \left( \frac{D}{4} \right)^2
\\
&= \frac{15}{16} D^2
\\
\therefore \ \
L &= \frac{\sqrt{15}}{4} D
\end{aligned}
\]
であり、これが求める \(L\) の最大値である。
(2)
1つの光源を中心とする半径 \(D\) の円を考える。
1つの受信機がこの円から出る瞬間に、その隣の隣の受信機がこの円に入るとすると、
\[
\begin{aligned}
L^2
&= D^2 - \left( \frac{D}{2} \right)^2
\\
&= \frac{3}{4} D^2
\\
\therefore \ \
L &= \frac{\sqrt{3}}{2} D
\end{aligned}
\]
であり、これが求める \(L\) の最大値である。
