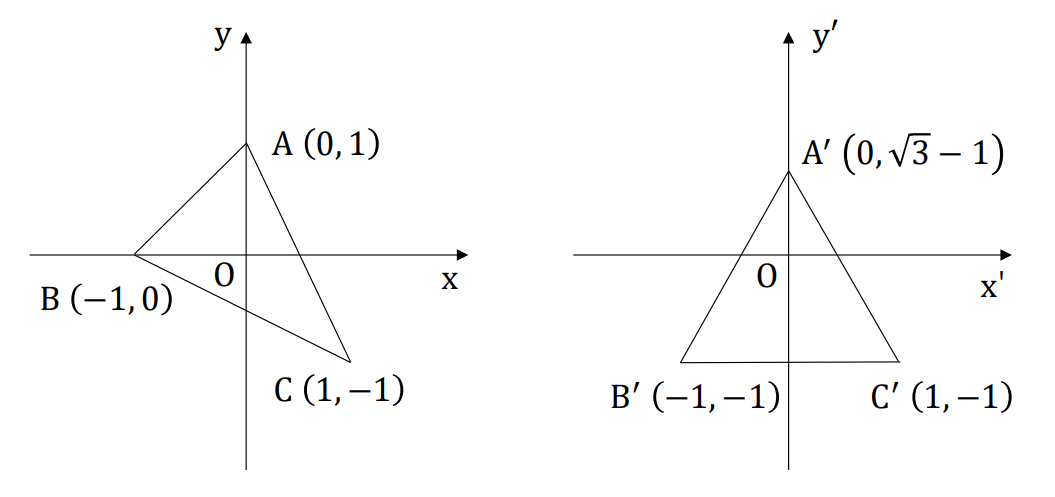Tokyo-University
東京大学 新領域創成科学研究科 海洋技術環境学専攻 2020年度
Author Miyake
Description 第1問
次の定積分を求めよ。
\[
I = \int_0^{\sqrt{3}} \frac{dx}{\sqrt{x^2 + 1}}
\]
第2問
整数 \(m\) 、任意の実数 \(\theta\) について、変数 \(x\) 、\(y\) を以下のように定義する。
\[
\left\{
\begin{aligned}
x(\theta) &= \sum_{m=0}^{\infty} \frac{\theta^{2m}}{(2m)!} \\
y(\theta) &= \sum_{m=0}^{\infty} \frac{\theta^{2m+1}}{(2m+1)!}
\end{aligned}
\right.
\]
ただし、\(m! \equiv m \times (m-1) \times (m-2) \times \cdots \times 2 \times 1\) 、\(0! = 1\) 、\(0^0 = 1\) である。
この時、以下の問いを答えよ。
1) \(\frac{dx}{dy}\) を \(x\) 、\(y\) で表せ。
2) \(x\) 、\(y\) の満たす関係を求めよ。
第3問
\[
A=\begin{pmatrix}
1 & 2 & 1 \\
2 & 5 & 6 \\
1 & 3 & 4\\
\end{pmatrix}
\]
について以下の問いに答えよ。
1) \(A^{-1}\) を求めよ。
2) \(|A^{-1}|= \frac{1}{|A|}\) となることを示せ。
第4問
座標系 \(\text{O}xy\) 上の三角形 \(ABC\) が、座標系 \(\text{O}x'y'\) 上の三角形 \(A'B'C'\) に変換された。
この時、座標系 \(\text{O}xy\) 上の任意の点 \(\vec{x}\) から座標系 \(\text{O}x'y'\) 上の点 \(\vec{x'}\) への変換を求めよ。
第5問
行列
\(A=\begin{pmatrix}
a & 1-a \\
1-a & a
\end{pmatrix}\)
について、以下の問いに答えよ。ただし \(a\) は実数で、\(0<a<1\) とする。
1) 固有値、固有ベクトルを求めよ。
2) \(A^n\) を求めよ。ただし、\(n\) は自然数である。
3) \(\lim_{n \rightarrow \infty} A^n\) を求めよ。
Kai 第1問
\[
\begin{aligned}
I &= \int_0^{\sqrt{3}} \frac{dx}{\sqrt{x^2 + 1}} \\
&= \left[ \log \left| x + \sqrt{x^2 + 1} \right|\right]_0^{\sqrt{3}} \\
&= \log \left( 2 + \sqrt{3} \right)
\end{aligned}
\]
第2問
1)
\[
\begin{aligned}
\frac{dx(\theta)}{d \theta}
&= \sum_{m=1}^\infty \frac{\theta^{2m-1}}{(2m-1)!}
\\
&= y(\theta)
\\
\frac{dy(\theta)}{d \theta}
&= \sum_{m=0}^\infty \frac{\theta^{2m}}{(2m)!}
\\
&= x(\theta)
\end{aligned}
\]
なので、\(\frac{dx}{dy} = \frac{\frac{dx}{d \theta}}{\frac{dy}{d \theta}} = \frac{y}{x}\)
を得る。
2)
\[
\begin{aligned}
x dx = y dy
\end{aligned}
\]
であり、これを積分すると、積分定数を \(C\) として、
\[
\begin{aligned}
x^2 = y^2 + C
\end{aligned}
\]
である。
\(\theta = 0\) のとき \(x=1, y=0\) なので、 \(C=1\) がわかり、
\[
\begin{aligned}
x^2 - y^2 = 1
\end{aligned}
\]
を得る。
第3問
1)
掃き出し法により、次のように求められる:
\[
\begin{aligned}
&
\begin{pmatrix}
1 & 2 & 1 & 1 & 0 & 0 \\
2 & 5 & 6 & 0 & 1 & 0 \\
1 & 3 & 4 & 0 & 0 & 1
\end{pmatrix}
\\
&
\begin{pmatrix}
1 & 2 & 1 & 1 & 0 & 0 \\
0 & 1 & 4 & -2 & 1 & 0 \\
0 & 1 & 3 & -1 & 0 & 1
\end{pmatrix}
\\
&
\begin{pmatrix}
1 & 0 & -7 & 5 & -2 & 0 \\
0 & 1 & 4 & -2 & 1 & 0 \\
0 & 0 & -1 & 1 & -1 & 1
\end{pmatrix}
\\
&
\begin{pmatrix}
1 & 0 & 0 & -2 & 5 & -7 \\
0 & 1 & 0 & 2 & -3 & 4 \\
0 & 0 & 1 & -1 & 1 & -1
\end{pmatrix}
\end{aligned}
\]
\[
\begin{aligned}
\therefore \ \
A^{-1}
=
\begin{pmatrix}
-2 & 5 & -7 \\
2 & -3 & 4 \\
-1 & 1 & -1
\end{pmatrix}
\end{aligned}
\]
2)
サラスの方法より、
\[
\begin{aligned}
|A|
&= (20+12+6)-(5+18+16)
\\
&= -1
\\
|A^{-1}|
&= (-6-20-14)-(-21-8-10)
\\
&= -1
\end{aligned}
\]
なので、
\(|A^{-1}| = 1 / |A|\) が成り立っていることがわかる。
第4問
\(\vec{x}=(x,y)\) から \(\vec{x'}=(x',y')\) への変換は次のように表される:
\[
\begin{aligned}
\begin{pmatrix} x \\ y \end{pmatrix}
=
\begin{pmatrix} a & b \\ c & d \end{pmatrix}
\begin{pmatrix} x' \\ y' \end{pmatrix}
+
\begin{pmatrix} e \\ f \end{pmatrix}
\end{aligned}
\]
点 A, B, C がそれぞれ 点 A', B', C' に変換されることから、
\[
\begin{aligned}
a = 1, b = 0, e = 0,
c = \frac{1}{\sqrt{3}},
d = \frac{2}{\sqrt{3}},
f = \frac{1}{\sqrt{3}} - 1
\end{aligned}
\]
がわかる。
つまり、
\[
\begin{aligned}
x' &= x
\\
y' &= \frac{x+2y+1-\sqrt{3}}{\sqrt{3}}
\end{aligned}
\]
である。
第5問
1)
\(A\) の固有値を \(\lambda\) とすると、
\[
\begin{aligned}
0
&= \det \begin{pmatrix} a-\lambda & 1-a \\ 1-a & a-\lambda \end{pmatrix}
\\
&= (\lambda - 1)(\lambda - 2a + 1)
\\
\therefore \ \
\lambda &= 1, 2a-1
\end{aligned}
\]
を得る。 \(a \ne 1\) なので、これらは相異なる固有値である。
固有値 \(1\) に属する固有ベクトルを求めるために
\[
\begin{aligned}
\begin{pmatrix} 0 \\ 0 \end{pmatrix}
&= \begin{pmatrix} a-1 & 1-a \\ 1-a & a-1 \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix}
\end{aligned}
\]
とおくと \(x=y\) であり、
固有値 \(2a-1\) に属する固有ベクトルを求めるために
\[
\begin{aligned}
\begin{pmatrix} 0 \\ 0 \end{pmatrix}
&= \begin{pmatrix} 1-a & 1-a \\ 1-a & 1-a \end{pmatrix}
\begin{pmatrix} x \\ y \end{pmatrix}
\end{aligned}
\]
とおくと \(x+y=0\) であるから、それぞれに属する固有ベクトルは例えば
\[
\begin{aligned}
\begin{pmatrix} 1 \\ 1 \end{pmatrix}
,
\begin{pmatrix} 1 \\ -1 \end{pmatrix}
\end{aligned}
\]
である。
2)
1) で求めた固有ベクトルを使って、
\[
\begin{aligned}
P
&= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}
\end{aligned}
\]
とおくと、
\[
\begin{aligned}
P^2 &= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
\\
PAP &= \begin{pmatrix} 1 & 0 \\ 0 & 2a-1 \end{pmatrix}
\end{aligned}
\]
が成り立つので、
\[
\begin{aligned}
A^n
&= P \begin{pmatrix} 1 & 0 \\ 0 & 2a-1 \end{pmatrix}^n P
\\
&= P \begin{pmatrix} 1 & 0 \\ 0 & (2a-1)^n \end{pmatrix} P
\\
&= \frac{1}{2} \begin{pmatrix}
1+(2a-1)^n & 1-(2a-1)^n \\ 1-(2a-1)^n & 1+(2a-1)^n
\end{pmatrix}
\end{aligned}
\]
を得る。
3)
\(0 \lt a \lt 1\) より \(-1 \lt 2a-1 \lt 1\) なので、
\(\lim_{n \to \infty} (2a-1)^n = 0\) であり、
\[
\begin{aligned}
\lim_{n \to \infty} A^n
&= \frac{1}{2} \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}
\end{aligned}
\]
を得る。