東京大学 新領域創成科学研究科 複雑理工学専攻 2020年度 専門基礎科目 第1問
Author
Miyake
Description
以下の間に答えよ。ただし, \(x,y,z,t,k\) は実数であるとする。
(間1)
関数 \(f(x,y) = x^3 + y^2 - xy\) の偏導関数 \(\frac{\partial f}{\partial x}\) と \(\frac{\partial f}{\partial y}\)を求めよ。また, 曲面 \(z = f(x,y)\) の \((x,y,z) = (1,2,f(1,2))\) における接平面の方程式を求めよ。
(間2)
関数 \(h(x) = \exp\{\exp(2x) - 1\}\) を \(x = 0\) のまわりで \(1\) 次の項までテイラー展開せよ。また, 極限
\[
a = \lim_{x \rightarrow 0} \frac{1 - h(x)}{x^k}
\]
が存在し, \(0 < |a| < \infty\) を満たすとき, \(k\) と \(a\) の値を求めよ.
(間3)
関数 \(\cos^{-1}\) は \(\cos\) の 逆関数で, \(\cos^{-1}\) の 定義域と値域は, それぞれ, \([-1,1]\) と \([0,\pi]\) であるとする。曲線 \(y = \cos^{-1}(x + \frac{1}{2})\) を描け。また, この曲線と \(x\) 軸および \(y\) 軸で囲まれる領域の面積を求めよ.
(間4)
実関数 \(g(t)\) が満たす次の微分方程式の一般解を求めよ.
\[
\frac{\text{d}^2g}{\text{d}t^2} + \frac{\text{d}g}{\text{d}t} + \sin t = 0
\]
また, 初期値 \(g(0) = 2,\frac{\text{d}g}{\text{d}t}(0)=0\) に対する特解を求めよ。
(間5)
\(D = \{(x,y)|0 \le 2x - y \le 1,0 \le x + 3y \le 2\}\) とする。
変数変換 \(u = 2x - y,v = x + 3y\) を用いて,次の重積分の値を求めよ。
\[
\iint_{D} \frac{(2x - y)^3}{4 + (x + 3y)^2}\text{d}x\text{d}y
\]
Kai
(問1)
偏導関数は、
\[
\begin{aligned}
\frac{\partial f}{\partial x} = 3x^2-y
, \ \ \ \
\frac{\partial f}{\partial y} = 2y-x
\end{aligned}
\]
である。
また、 \(x=1,y=2\) のとき、
\[
\begin{aligned}
f(1,2)=3
, \ \ \ \
\frac{\partial f}{\partial x} (1,2) = 1
, \ \ \ \
\frac{\partial f}{\partial y} (1,2) = 3
\end{aligned}
\]
であるから、
求める接平面は、点 \((1,2,3)\) を通り、法線ベクトル \((1,3,-1)\) を持つので、
その方程式は、
\[
\begin{aligned}
(x-1) + 3(y-2) - (z-3) = 0
\end{aligned}
\]
\[
\begin{aligned}
\therefore \ \ \ \
x + 3y - z - 4 = 0
\end{aligned}
\]
である。
(問2)
次のように計算できる:
\[
\begin{aligned}
h'(x) &= \exp \left\{ \exp (2x) - 1 \right\}
\cdot \exp (2x) \cdot 2
\\
h(0) &= 1
\\
h'(0) &= 2
\end{aligned}
\]
よって、 \(h(x)\) は1次の項までで次のようにテイラー展開される:
\[
\begin{aligned}
h(x) = 1 + 2x + \cdots
\end{aligned}
\]
\(h(x)\) の2次以上の項をまとめて \(\varphi(x)\) とすると、
\[
\begin{aligned}
a
&= \lim_{x \to 0} \frac{1 - h(x)}{x^k}
\\
&= \lim_{x \to 0} \frac{-2x - \varphi(x)}{x^k}
\end{aligned}
\]
であるから、 \(k \lt 1\) のときは \(a=0\) であり、 \(k \gt 1\) のときは発散する。
よって、極限が存在し \(0 \lt |a| \lt \infty\) を満たすのは
\(k=1\) のときであり、このとき
\[
\begin{aligned}
a = -2
\end{aligned}
\]
である。
(問3)
グラフは、このようになります。
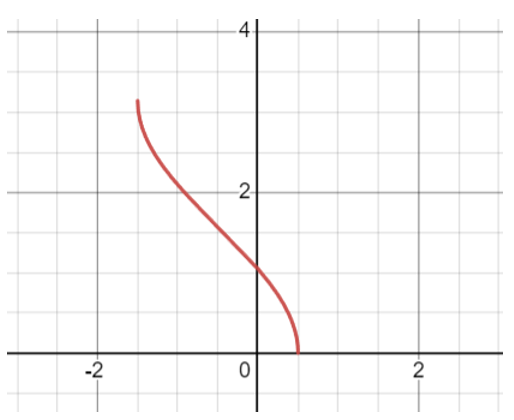
求める面積は、
\[
\begin{aligned}
\int_0^{1/2} \cos^{-1} \left( x + \frac{1}{2} \right) dx
= \int_0^{\pi / 3} \left( \cos x - \frac{1}{2} \right) dx
= \left[ \sin x - \frac{1}{2} x \right]_0^{\pi / 3}
= \frac{\sqrt{3}}{2} - \frac{\pi}{6}
\end{aligned}
\]
である。
(問4)
\(h(t) = dg(t)/dt\) とすると、与えられた微分方程式は、次のように書ける:
\[
\begin{align}
\frac{dh(t)}{dt} + h(t) + \sin t = 0
\tag{1} \label{1}
\end{align}
\]
そこで、
\[
\begin{aligned}
\frac{dh(t)}{dt} + h(t) = 0
\end{aligned}
\]
を考えると、これの一般解は、積分定数を \(A\) として、
\[
\begin{aligned}
h(x) = A e^{-t}
\end{aligned}
\]
と書ける。
そこで、式 (\(\ref{1}\)) の解を次のよう形で探す:
\[
\begin{aligned}
h(x) = A(t) e^{-t}
\end{aligned}
\]
これを式 (\(\ref{1}\)) に代入して整理すると、
\[
\begin{aligned}
A'(t) = - e^t \sin t
\end{aligned}
\]
よって、
\[
\begin{aligned}
A(t) = - \int e^t \sin t dt
= - e^t \sin t + \int e^t \cos t dt
= - e^t \sin t + e^t \cos t - \int e^t \sin t dt
\end{aligned}
\]
よって、
\[
\begin{aligned}
A(t) &= \frac{1}{2} \left( \cos t - \sin t \right) e^t + B
\\
\therefore \ \
h(t) &= \frac{1}{2} \left( \cos t - \sin t \right) + B e^{-t}
\\
\therefore \ \
g(t) &= \frac{1}{2} \left( \sin t + \cos t \right) - B e^{-t} + C
\end{aligned}
\]
ここで、 \(B, C\) は積分定数である。
また、与えられた初期値を満たすのは、
\[
\begin{aligned}
B = - \frac{1}{2}
, \ \
C = 1
\end{aligned}
\]
すなわち、
\[
\begin{aligned}
g(t) = \frac{1}{2} \left( \sin t + \cos t \right) + \frac{1}{2} e^{-t} + 1
\end{aligned}
\]
である。
(問5)
与えられた変数変換について、
\[
\begin{aligned}
\frac{\partial u}{\partial x} = 2
&, \ \
\frac{\partial u}{\partial y} = -1
\\
\frac{\partial v}{\partial x} = 1
&, \ \
\frac{\partial v}{\partial y} = 3
\end{aligned}
\]
であるから、 \(du dv = 7 dx dy\) であり、
与えられた積分は、
\[
\begin{aligned}
&\iint_D \frac{u^3}{4+v^2} \frac{du dv}{7}
= \frac{1}{7} \int_0^1 u^3 du \int_0^2 \frac{dv}{4+v^2}
\\
&= \frac{1}{7} \left[ \frac{u^4}{4} \right]_0^1
\left[ \frac{1}{2} \arctan \frac{v}{2} \right]_0^2
= \frac{1}{7} \frac{1}{4} \frac{1}{2} \frac{\pi}{4}
= \frac{\pi}{224}
\end{aligned}
\]
となる。
