東京大学 工学系研究科 2017年度 数学 第4問

Author

Description

\(0 \leq \theta < 2\pi ,0 \leq \alpha \leq \pi\) 範囲にある実数 \(\theta\), \(\alpha\) に対して, 3 次元直交座標系 \(xyz\) における点 \(P(\cos\theta,\sin\theta,1)\) と点 \(Q(\cos(\theta + \alpha),\sin(\theta + \alpha),-1)\) の 2 点を通る直線 \(L\) を考える。

I.

直線 \(L\) を,　媒介変数 \(t\) の一次式として表せ。ただし, \(t = 0\) の時に点 \(Q\) を,　\(t = 1\) の時に点 \(P\) を表すように定めよ。

II.

\(\theta\) を \(0 \leq \theta < 2\pi\) の範囲で変化させたときに直線 \(L\) が描く曲面 \(S\) を \(x,y,z\) の方程式として求めよ。また, 曲面 \(S\)と平面 \(y=0\) の交線を \(C\) とする。\(C\) を \(x,z\) の方程式として求め, その概形を図示せよ。

次に, 曲面 \(S\) のガウス曲率を考える。一般に曲面上の点 \(R\) の位置ベクトル \(r\) が媒介変数 \(u,v\) を用いて,

\[ \begin{align} r(u,v) = (x(u,v),y(u,v),z(u,v)) \end{align} \]

で与えられるとき,　ガウス曲率 \(K\) は次式のように表される。

\[ \begin{align} K = \frac{(r_{uu}\cdot e)(r_{vv}\cdot e) - (r_{uv} \cdot e)^2}{(r_{u}\cdot r_{u})(r_{v}\cdot r_{v})- (r_{u} \cdot r_{v})^2} \end{align} \]

ここで, \(r_{u},r_{v}\)と\(r_{uu},r_{uv},r_{vv}\) は媒介変数 \(u,v\) に関する \(r(u,v)\) の一階偏微分,　二階偏微分を表している。また, \(\big( a \cdot b \big)\) は 3 次元ベクトル \(a,b\) の内積, \(e\) は点 \(R\) における法線方向の単位ベクトルを表している。

III.

曲面 \(S\) と \(x\) 軸の交点のうち領域 \(x>0\) にあるものを点 \(W\) とする。\(0 \leq \alpha < \pi\) を満たす \(\alpha\) に対し,　点 \(W\) における曲面 \(S\) のガウス曲率を計算せよ。

IV.

\(0 \leq \alpha < \pi\) を満たす \(\alpha\) に対し,　曲面 \(S\) の任意の点においてガウス曲率が \(0\) 以下であることを示せ。

Kai

I.

直線 \(L\) 上の点 \(M\) は,

\[ \overrightarrow{OM} = \overrightarrow{OQ} + t\overrightarrow{QP} \]

と表せる。このとき, \(t = 0\) で \(\overrightarrow{OQ}\), \(t = 1\) で \(\overrightarrow{OQ} + \overrightarrow{QP} = \overrightarrow{OP}\) となり, 題意た満たす。

\[ \overrightarrow{QP} = (\cos\theta - \cos(\theta + \alpha),\sin\theta - \sin(\theta + \alpha), 2) \]

であるから,　求める直線 \(L\) の媒介変数表示は,

\[ L: \left\{ \begin{aligned} x &= \cos(\theta + \alpha) + t(\cos\theta - \cos(\theta + \alpha)) \\ y &= \sin(\theta + \alpha) + t(\sin\theta - \sin(\theta + \alpha)) \\ z &= -1 + 2t \\ \end{aligned} \right. \]

II.

和積の公式より,

\[ \begin{aligned} x &= \cos(\theta + \alpha) - 2t\sin\bigg(\frac{\theta + (\theta + \alpha)}{2}\bigg) \sin\bigg(\frac{\theta - (\theta + \alpha)}{2}\bigg) \\ &= \cos(\theta + \alpha) + 2t\sin(\theta + \frac{\alpha}{2})\sin\frac{\alpha}{2} \\ y &= \sin(\theta + \alpha) + 2t\cos\bigg(\frac{\theta + (\theta + \alpha)}{2}\bigg)\sin\bigg(\frac{\theta - (\theta + \alpha)}{2}\bigg) \\ &= \sin(\theta + \alpha) - 2t\cos(\theta + \frac{\alpha}{2})\sin\frac{\alpha}{2} \end{aligned} \]

\(x^2 + y^2\) を計算してを消去する。

\[ \begin{aligned} &\quad x^2 + y^2 \\ &= \cos^2(\theta + \alpha) + 4t\cos(\theta + \alpha)\sin\big(\theta + \frac{\alpha}{2}\big)\sin\frac{\alpha}{2} \\ &\quad + 4t^2\sin^2\big(\theta + \frac{\alpha}{2}\big)\sin^2\frac{\alpha}{2} + \sin^2(\theta + \alpha) \\ &\qquad - 4t\sin(\theta + \alpha)\cos\big(\theta + \frac{\alpha}{2}\big)\sin\frac{\alpha}{2} \\ &\quad \qquad + 4t^2\cos^2\big(\theta + \frac{\alpha}{2}\big)\sin^2\frac{\alpha}{2} \\ &= 1 + 4t^2\sin^2 \frac{\alpha}{2} + 4t\sin\frac{\alpha}{2} \\ &\qquad\cdot \big(\cos(\theta + \alpha)\sin\big(\theta + \frac{\alpha}{2}\big) - \sin(\theta + \alpha)\cos\big(\theta + \frac{\alpha}{2}\big) \big) \\ &= 1 + 4t^2\sin^2\frac{\alpha}{2} + 4t\sin\frac{\alpha}{2}\sin\big(\theta + \frac{\alpha}{2} - (\theta + \alpha)\big) \quad (\because \text{加法定理}) \\ &= 1 + 4t^2\sin^2\frac{\alpha}{2} - 4t\sin^2\frac{\alpha}{2} \end{aligned} \]

さらに, \(t = (z + 1)/2\) を代入して \(t\) を消去すると,

\[ \begin{aligned} x^2 + y^2 &= 1 + (z + 1)^2 \sin^2\frac{\alpha}{2} - 2(z + 1)\sin^2\frac{\alpha}{2} \\ &= \sin^2\frac{\alpha}{2} \cdot z^2 + 1 - \sin^2\frac{\alpha}{2} \\ &= \sin^2\frac{\alpha}{2} \cdot z^2 + \cos^2\frac{\alpha}{2} \end{aligned} \]

よって,　求める曲面 \(S\) の方程式は

\[ x^2 + y^2 - \sin^2\frac{\alpha}{2} \cdot z^2 = \cos^2\frac{\alpha}{2} \]

また \(y = 0\) とすると, 交線 \(C\) の方程式を得る。

\[ x^2 - \sin^2\frac{\alpha}{2} \cdot z^2 = \cos^2\frac{\alpha}{2} \]

\(a = 0\) のとき,　\(x = \pm 1\) である。

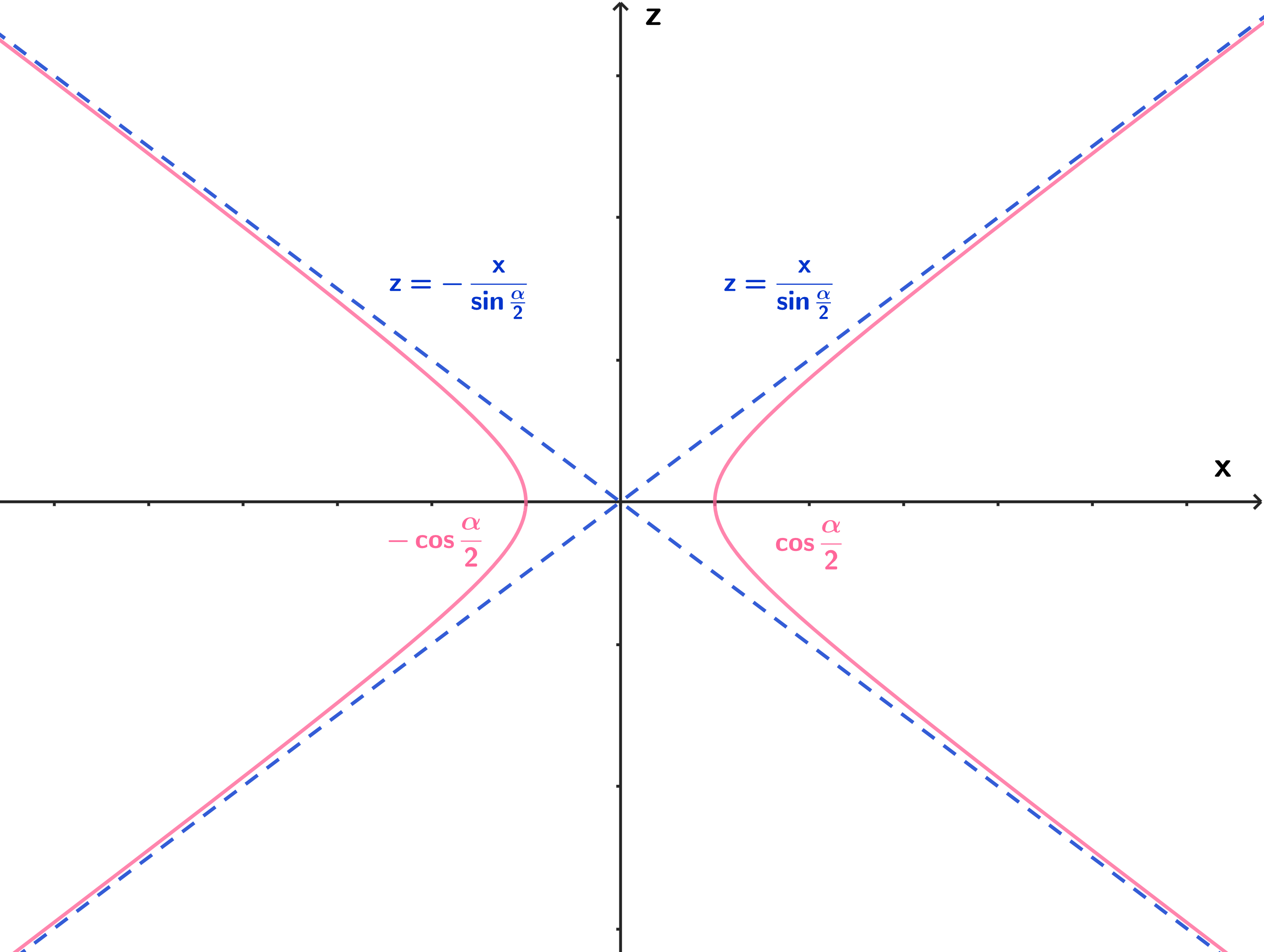
\(a \neq 0\) のとき,　この曲線は双曲線であり,　その漸近線の方程式は,　

\[ z = \pm \frac{\cos\frac{\alpha}{2}}{\sin\frac{\alpha}{2}} \cdot \frac{1}{\cos\frac{\alpha}{2}} x = \pm \frac{x}{\sin\frac{\alpha}{2}} \]

である。概形は次のようになる。

今,　曲面 \(S\) 上の点 \(R\) の位置ベクトルは媒介変数 \(\theta ,t\) を用いて以下のように表されでおり,

\[ r(\theta ,t) = \begin{pmatrix} \cos(\theta + \alpha) + t(\cos\theta - \cos(\theta - \alpha)) \\ \sin(\theta + \alpha) + t(\sin\theta - \sin(\theta + \alpha)) \\ -1 + 2t \end{pmatrix} \]

ガウス曲率 \(K\) は,

\[ K = \frac{(r_{\theta\theta}\cdot e)(r_{tt}\cdot e) - (r_{\theta t}\cdot e)^2}{(r_{\theta}\cdot r_{\theta})(r_{t} \cdot r_{t}) - (r_{\theta} \cdot r_{t})^2} \]

で表される。

\[ \begin{aligned} r_{\theta} &= \begin{pmatrix} -(1 - t)\sin(\theta + \alpha) - t\sin \theta \\ (1 - t)\cos(\theta + \alpha) + t\cos \theta \\ 0 \end{pmatrix} \\ r_{t} &= \begin{pmatrix} \cos \theta - \cos(\theta + \alpha) \\ \sin \theta - \sin(\theta + \alpha) \\ 2 \end{pmatrix} \\ r_{\theta\theta} &= \begin{pmatrix} -(1 - t)\cos(\theta + \alpha) - t\cos\theta \\ -(1 - t)\sin(\theta + \alpha) -t\sin\theta \\ 0 \end{pmatrix} \\ r_{tt} &= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \\ r_{\theta t} &= \begin{pmatrix} -\sin\theta + \sin(\theta + \alpha) \\ \cos\theta - \cos(\theta + \alpha) \\ 0 \end{pmatrix} \end{aligned} \]

計算の都合上, 設問 IV から先に解答する。

III.

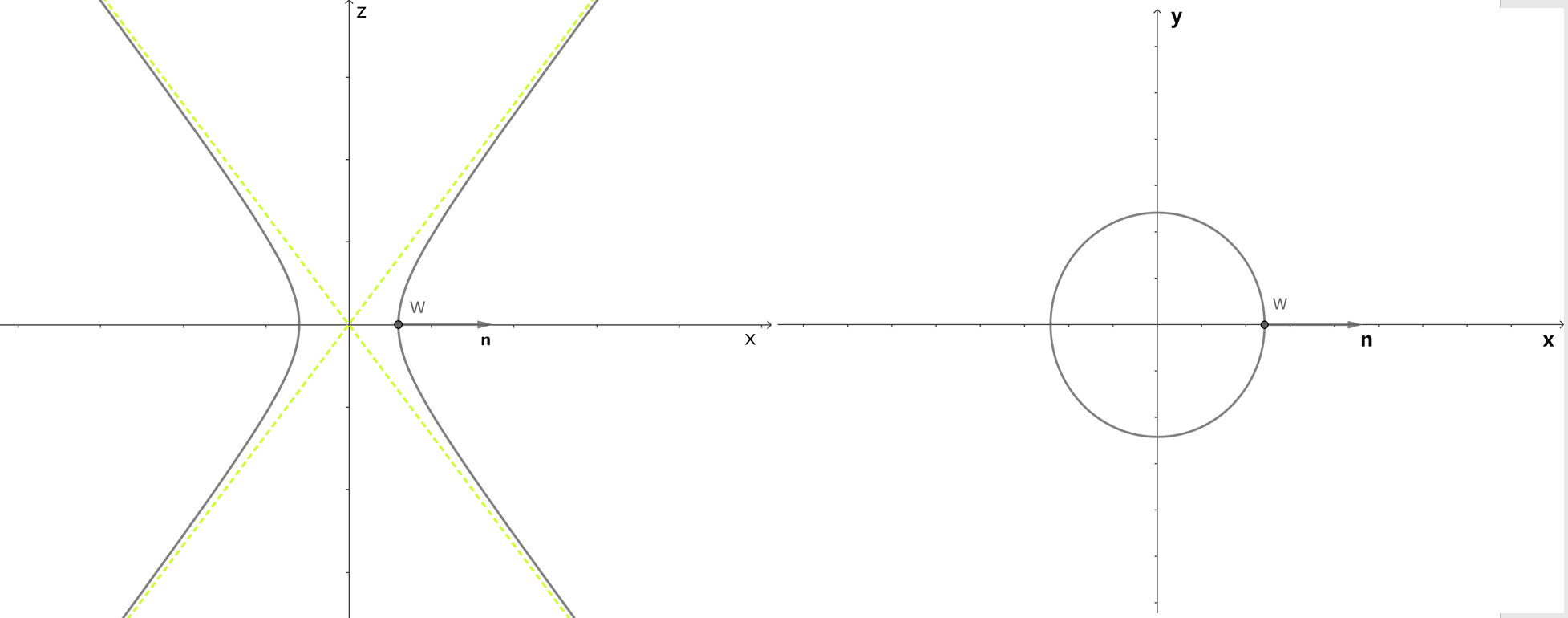
設問 II の図を利用して, 点 \(W\) における曲面 \(S\) の法線ベクトル \(n\) を求める。 平面 \(y = 0\) での断面が下図左であり, これが双曲線であることから \(n\) は実数 \(k\) を用いて \((1,k,0)\) の形で表すことができる。

一方で, 平面 \(z = 0\) で断面は \(S\) の方程式に \(z = 0\) を代入することで, 原点を中心とする半径 \(\cos\frac{\alpha}{2}\) の円 (下図右) であることが容易に分かる。したがって, \(n\) は実数 \(l\) を用いて \((1,0,l)\) の形で表すことができる。

これらをともに満たす \(n\) は, \(n=(1,0,0)\) であり, これは単位ベクトルだから点 \(W\) における単位法線ベクトル \(e\) は \(e=(1,0,0)\) となる。

点 \(W\) において, \(\theta,t\) は以下の関係を満たす。

\[ \left\{ \begin{aligned} \cos(\theta + \alpha) + t(\cos\theta - \cos(\theta + \alpha)) &= \cos\frac{\alpha}{2 } \\ \sin(\theta + \alpha) + t(\sin\theta - \sin(\theta + \alpha)) &= 0 \\ -1 + 2t &= 0 \end{aligned} \right. \]

3つ目の式より \(t = 1/2\) であり, 2つ目の式に代入して,

\[ \sin\theta + \sin(\theta + \alpha) = 0 \]

\[ \sin \big((\theta + \frac{\alpha}{2}) - \frac{\alpha}{2}\big) + \sin \big((\theta + \frac{\alpha}{2} + \frac{\alpha}{2})\big) = 0 \]

\[ 2\cos\frac{\alpha}{2}\sin\big(\theta + \frac{\alpha}{2}\big) = 0 (\because\text{和積の公式}) \]

\(\cos\frac{\alpha}{2} \neq 0\)より, \(\sin(\theta + \frac{\alpha}{2}) = 0\)

\[ \therefore \theta + \frac{\alpha}{2} =n\pi \quad (n=1,\pm1,\pm2,\cdots) \]

\(0 \leq \alpha < \pi\), \(0 \leq \theta < 2\pi\) より,

\[ \theta = -\frac{\alpha}{2} + \pi ,-\frac{\alpha}{2} + 2\pi \]

\[ \therefore \sin\theta = \pm\sin\frac{\alpha}{2} \Leftrightarrow \sin^2\theta =\sin^2\frac{\alpha}{2} \]

\(K\) の分子は,

\[ \begin{aligned} &\quad -(r_{\theta t}\cdot e)^2 \\ &= -(\sin(\theta + \alpha) - \sin\theta)^2 \\ &= -(\sin(\theta + \alpha) + \sin\theta)^2 + 4\sin\theta\sin(\theta + \alpha) \\ &= -0^2 + 4\sin\theta \cdot (-\sin\theta) \\ &= -4\sin^2\theta = -4\sin^2\frac{\alpha}{2} \end{aligned} \]

\(K\) の分母は,

\[ \begin{aligned} &\quad (r_{\theta} \cdot r_{\theta})(r_{t} \cdot r_{t}) - (r_{\theta} \cdot r_{t})^2 \\ &= (6 - 2\cos\alpha)(2 - 2\cos\alpha)(t - \frac{1}{2})^2 + 2(1 + \cos\alpha) \\ &= 0 + 2 \cdot 2\cos^2\frac{\alpha}{2} = 4\cos^2\frac{\alpha}{2} \end{aligned} \]

したがって求めるガウス曲率 \(K\) は,

\[ K = \frac{-4\sin^2\frac{\alpha}{2}}{4\cos^2\frac{\alpha}{2}} = -\tan^2\frac{\alpha}{2} \]

IV.

\(r_{tt} = o\) であることから, \(K\) の分子は \(-(r_{\theta t} \cdot e)^2\) であり, これは明らかに \(0\) 以下である。従って, \(K\) の分母が正であることを示せば良い。

\[ \begin{aligned} &\quad r_{\theta} \cdot r_{\theta} \\ &= \{(1 - t)\sin(\theta + \alpha) + t\sin\theta\}^2 + \{(1 - t)\cos(\theta + \alpha) + t\cos\theta\}^2 \\ &= (1 - t)^2 + t^2 + 2t(1 - t)\{\sin(\theta + \alpha)\sin\theta + \cos(\theta + \alpha)\cos\theta\} \\ &= 1 - 2t + 2t^2 + 2t(1 - t)\cos\big((\theta + \alpha) - \theta\big) \\ &= 1 - 2t + 2t^2 + 2t(1 - t)\cos\alpha \end{aligned} \]

\[ \begin{aligned} &\quad r_{t} \cdot r_{t} \\ &= (\cos\theta - \cos(\theta + \alpha))^2 + (\sin\theta - \sin(\theta + \alpha))^2 + 2^2 \\ &= 1 + 1 + 4 - 2\{\cos(\theta + \alpha)\cos\theta\ + \sin\theta\sin(\theta + \alpha)\} \\ &= 6 - 2\cos\alpha \end{aligned} \]

\[ \begin{aligned} &\quad r_{\theta} \cdot r_{t}\\ &= \{-(1 - t)\sin(\theta + \alpha) - t\sin\theta\}(\cos\theta - \cos(\theta + \alpha)) \\ &\qquad +\{(1 - t)\cos(\theta + \alpha)+ t\cos\theta\}(\sin\theta - \sin(\theta + \alpha)) \\ &= -(1 - t)\sin(\theta + \alpha)\cos\theta + (1 - t)\sin(\theta + \alpha)\cos(\theta + \alpha)\\ &\qquad - t\sin\theta\cos\theta + t\sin\theta\cos(\theta + \alpha) + (1 - t)\cos(\theta + \alpha)\sin\theta \\ &\quad \qquad - (1 - t)\cos(\theta + \alpha)\sin(\theta + \alpha) \\ &\qquad \qquad + t\sin\theta\cos\theta - t\cos\theta\sin(\theta + \alpha) \\ &= -\sin(\theta + \alpha)\cos\theta + \cos(\theta + \alpha)\sin\theta \\ &= \sin(\theta - (\theta + \alpha))\\ &= -\sin\alpha \end{aligned} \]

であるから, \(K\) の分母は,

\[ \begin{aligned} &\quad (r_{\theta} \cdot r_{\theta})(r_{t} \cdot r_{t}) - (r_{\theta} \cdot r_{t})^2 \\ &= \{1 - 2t + 2t^2 + 2t(1 - t)\cos\alpha\}(6 - 2\cos\alpha) - \sin^2\alpha \\ &= (6 - 2\cos\alpha)\{(2 - 2\cos\alpha)t^2 + (2\cos\alpha - 2)t + 1\} - (1 - \cos^2\alpha) \\ &= (6 - 2\cos\alpha)(2 - 2\cos\alpha)\big(t - \frac{1}{2}\big)^2 \\ &\qquad \qquad - \frac{1}{4}(6 - 2\cos\alpha)(2 - 2\cos\alpha) + (5 - 2\cos\alpha + \cos^2\alpha) \\ &= (6 - 2\cos\alpha)(2 - 2\cos\alpha)\big(t - \frac{1}{2}\big)^2 + 2(1 + \cos\alpha) \end{aligned} \]

ここで, \(0 \leq \alpha < \pi\) より, \(\cos\alpha \ge 0\) であるから,

\[ (r_{\theta} \cdot r_{\theta})(r_{t} \cdot r_{t}) - (r_{\theta} \cdot r_{t})^2 > 0 \]

である。したがって, \(K \leq 0\) が示された。