東京大学 工学系研究科 電気系工学専攻 2022年度 問題4 情報工学II

Author

donguri0912

Description

I.

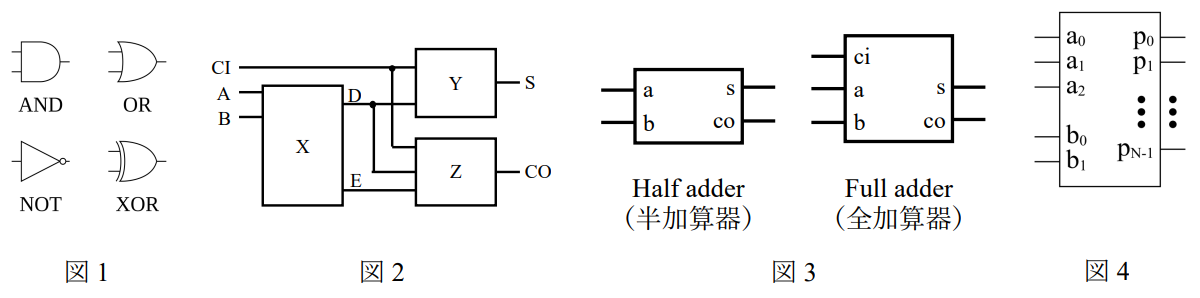
論理回路に関する以下の問に答えよ．回路図に使⽤する論理ゲートを図 \(1\) に⽰す．AND, ORゲートの伝搬遅延時間がそれぞれ \(50\) ps, NOTゲートの伝搬遅延時間が \(30\) ps, XORゲートの伝搬遅延時間が \(80\) psで，配線遅延は無視できるものとする．なお，クリティカルパス（⼊⼒から出⼒までの伝搬遅延時間が最も⼤きい経路）は⼊⼒と出⼒の組で⽰し，複数ある場合はすべて⽰すこと．

(1) 図 \(2\) は，⼊⼒ A, B を，キャリー（桁上げ）⼊⼒ CI を考慮して加算し，和 S とキャリー出⼒ CO を⽣成する全加算器である．

• (1-i) 図 \(2\) の X は，A, B の和 D とキャリー出⼒ E を⽣成する半加算器である．D, E の真理値表を⽰せ．また，図 \(1\) の AND, OR, NOT ゲートのみを⽤いて X の回路を⽰し，クリティカルパスとその遅延を⽰せ．
• (1-ii) 図 \(1\) のすべてのゲートが使⽤できるとき，クリティカルパスの伝搬遅延時間がより⼩さい X の回路を⽰せ．また，クリティカルパスとその伝搬遅延時間を⽰せ．
• (1-iii) Y，Z について，CI, D, E を⼊⼒，S, CO を出⼒とする真理値表を⽰し，クリティカルパスの伝搬遅延時間が最⼩となる回路を⽰せ．図 \(1\) のすべてのゲートを使⽤してよい．また，X に問(1-ii)の回路を使⽤した場合のこの全加算器のクリティカルパスとその伝搬遅延時間を⽰せ．

以下では，半加算器は問(1-ii)で作成したもの，全加算器は問(1-iii)で作成したものを使⽤する．

(2) 全加算器を⽤いてキャリー⼊⼒を持つ符号なし \(3\) ビット加算器を作成し，回路図を⽰せ．また，クリティカルパスとその伝搬遅延時間を⽰せ．\(2\) 組の \(3\) ビットの⼊⼒を \(a_2a_1a_0\) と \(b_2b_1b_0\)，キャリー⼊⼒を ci，和を \(s_2s_1s_0\)，キャリー出⼒を coとする．全加算器の記号は図 \(3\) のものを⽤いよ．

(3) 図 \(４\) に⽰す，\(3\) ビットの⼊⼒ \(a_2a_1a_0\)と \(2\) ビットの⼊⼒ \(b_1b_0\) とを持つ符号なし乗算器を考える．

• (3-i) 積 p のビット幅 N を答えよ．
• (3-ii) 半加算器，全加算器を少なくともひとつずつ使⽤してこの乗算器を作成し，回路図を⽰せ．ただし，クリティカルパスの伝搬遅延時間をなるべく⼩さくすること．図 \(1\) ，図 \(3\) のすべての記号を⽤いてよい．また，クリティカルパスとその伝搬遅延時間を⽰せ．

II.

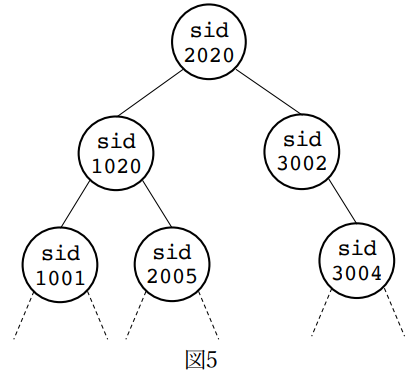
学生の学籍番号（sid）を，\(2\) 分探索木を用いて管理する C 言語のプログラムを考える．\(2\) 分探索木は，図 \(5\) のように，各ノードに最大 \(2\) 個の子ノードが接続された木構造であり，ノードの値は，左の子ノードの値より大きく右の子ノードの値より小さいという制約がある．学籍番号を持つノードをプログラム \(1\) の構造体で表現する．以下の問に答えよ．

(1) プログラム \(2\) に，新しい sid を持つノードを追加する関数 add() を⽰す．空欄 A, B, C を埋めて完成させよ．

(2) 空の⽊に add() を使い以下の順で新しいノードを追加したときの \(2\) 分探索⽊を図 \(5\) の例に倣って書け．

• (2-i) sid = 1040, 1042, 2001, 2004, 2010, 2012
• (2-ii) sid = 2001, 1042, 2010, 1040, 2004, 2012

(3) プログラム \(3\) に sid を⼩さい順に列挙する関数 enumerate() を⽰す．空欄 D, E, F, G を埋めて完成させよ．

(4) ノードを \(2\) 分探索⽊から削除する⼿順を，削除したいノードの⼦ノードが \(0\) 個，\(1\) 個，\(2\) 個の場合について簡潔に説明せよ．

(5) 既に \(2\) 分探索⽊上に存在するノードと同じ sid を持つノードを追加しようとした時の add() の振る舞いと問題点を簡潔に説明せよ．

(6) 追加する sid をあらかじめ⽤意された⼗分に⼤きな配列に先頭から追加順に格納する⽅法と⽐べ，\(2\) 分探索⽊を⽤いる利点と⽋点をそれぞれ簡潔に述べよ．その際，探索，要素の追加のそれぞれに必要な計算量のオーダーについて⾔及せよ．

/* プログラム1 */
typedef struct node {
    int sid;struct node *left;struct node *right;
} node_t;

/* プログラム2 */
node_t *add(node_t *root, node_t *new){
    if(root == NULL){
        return   A   ;
    }

    if(root->sid > new->sid){
           B   ;
    }
    else if(root->sid < new->sid){
           C   ;
    }
    return root;
}

/* プログラム3 */
void enumerate(node_t *root){
    if(   D   ){
           E   ;
    }
    printf("%d¥n", root->sid);
    if(   F   ){
           G   ;
    }
    return;
}

Kai

I.

(1)

(1-i)

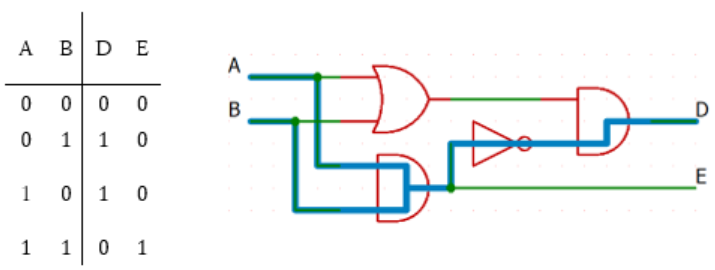
クリティカルパスは太線で示した \(2\) 経路。

遅延は共に \(50 \text{ps}+ 30 \text{ps}+50 \text{ps}=130 \text{ps}\)

(1-ii)

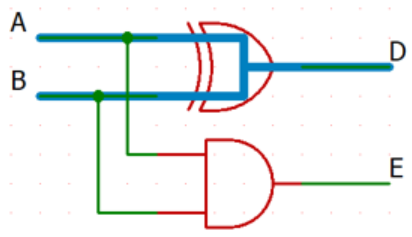
クリティカルパスは太線で示した \(2\) 経路。

遅延は共に \(80 \text{ps}\)

(1-iii)

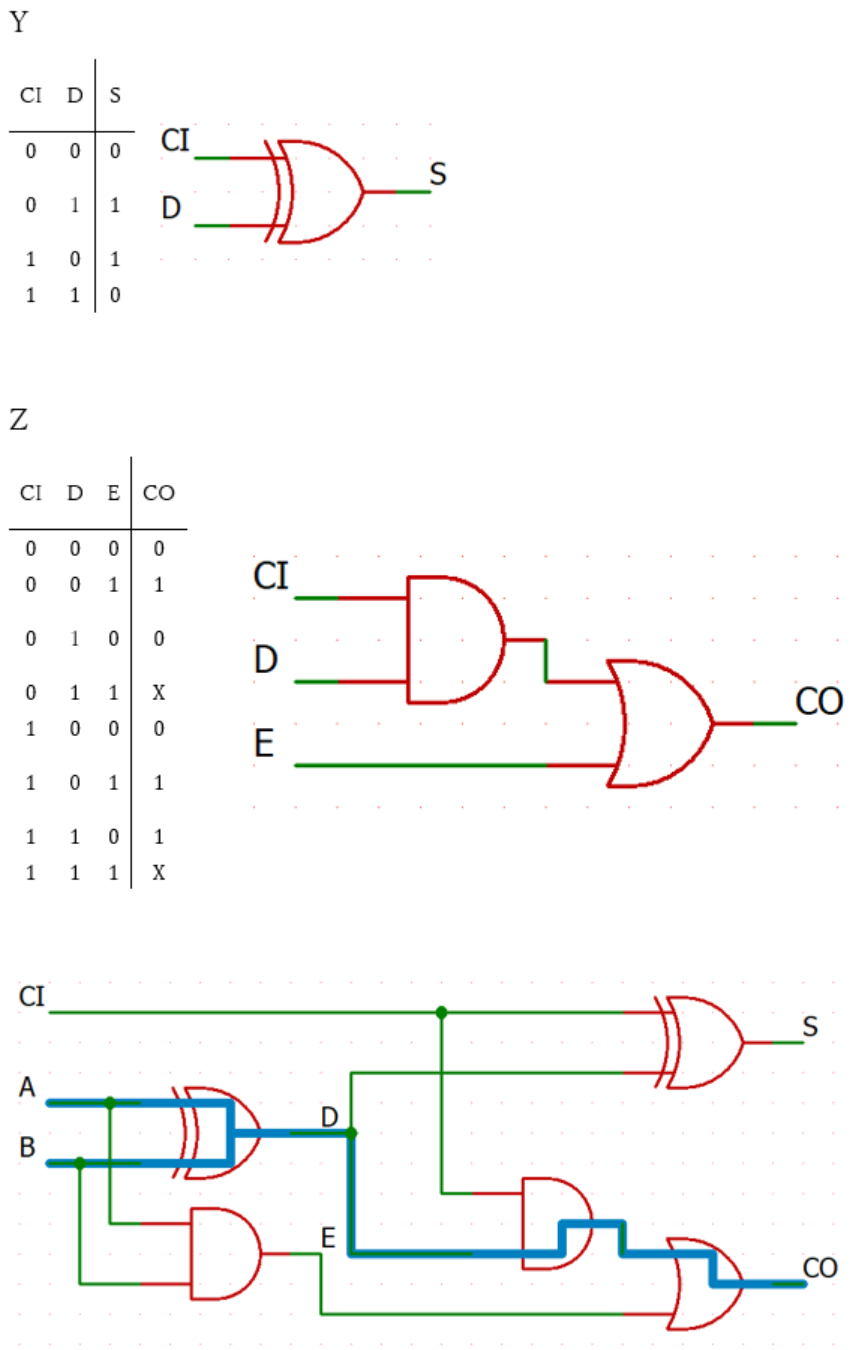
クリティカルパスは太線で示した \(2\) 経路。

遅延は共に \(80\text{ps}+ 50\text{ps} + 50\text{ps}=180\text{ps}\)

(2)

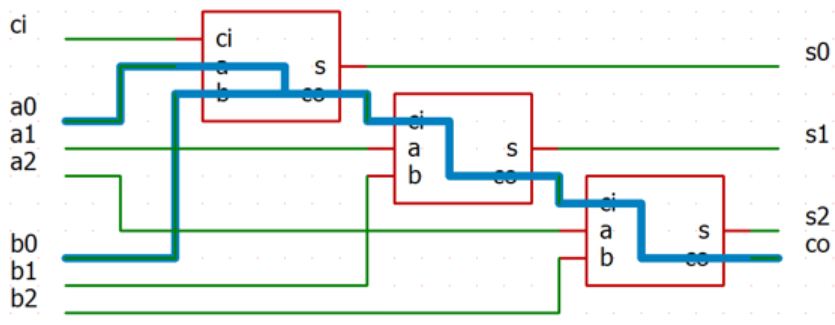
クリティカルパスは太線で示した \(2\) 経路。

(1-iii) の全加算器で CI から CO の伝搬遅延時間は \(50\text{ps}+50\text{ps}=100\text{ps}\) なので、

これらのクリティカルパスの伝搬遅延時間は共に \(180\text{ps}+ 100\text{ps}+100\text{ps}=380\text{ps}\)

(3)

(3-i)

\(2\)ビットの \(2\) 進数の最大値は \(11_2 = 3\)、\(3\) ビットの \(2\) 進数の最大値は \(111_2 = 7\)。

よって積 \(p\) の最大値は \(3 \times 7 = 21 = 10101_2\)

よって \(N = 5\)

(3-ii)

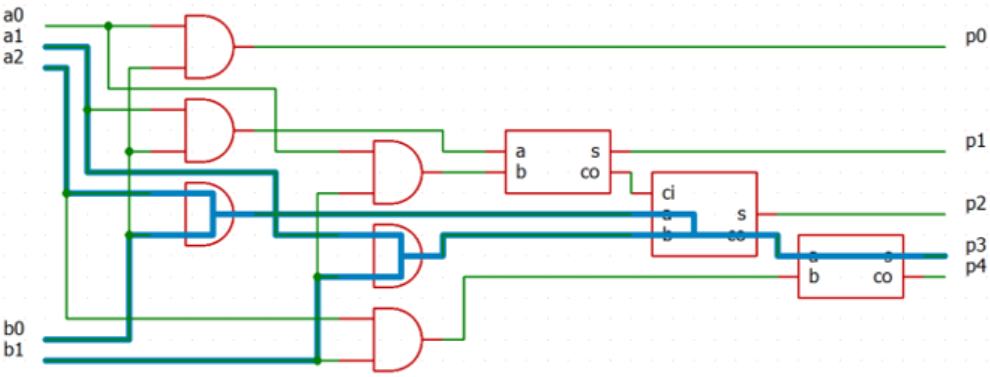
クリティカルパスは太線で示した \(4\) 経路。

(1-ii) の全加算器で A から CO の伝搬遅延時間は \(50\text{ps}\) なので、

これらのクリティカルパスの伝搬遅延時間は共に \(50\text{ps}+180\text{ps}+80\text{ps}=310\text{ps}\)

II.

(1)

解答は分かりやすいよう空欄だけでなくその行ごと書いてある。

// A
return new;
// B
root->left = add(root->left);
// C
root->right = add(root->right);

(2)

(2-i)

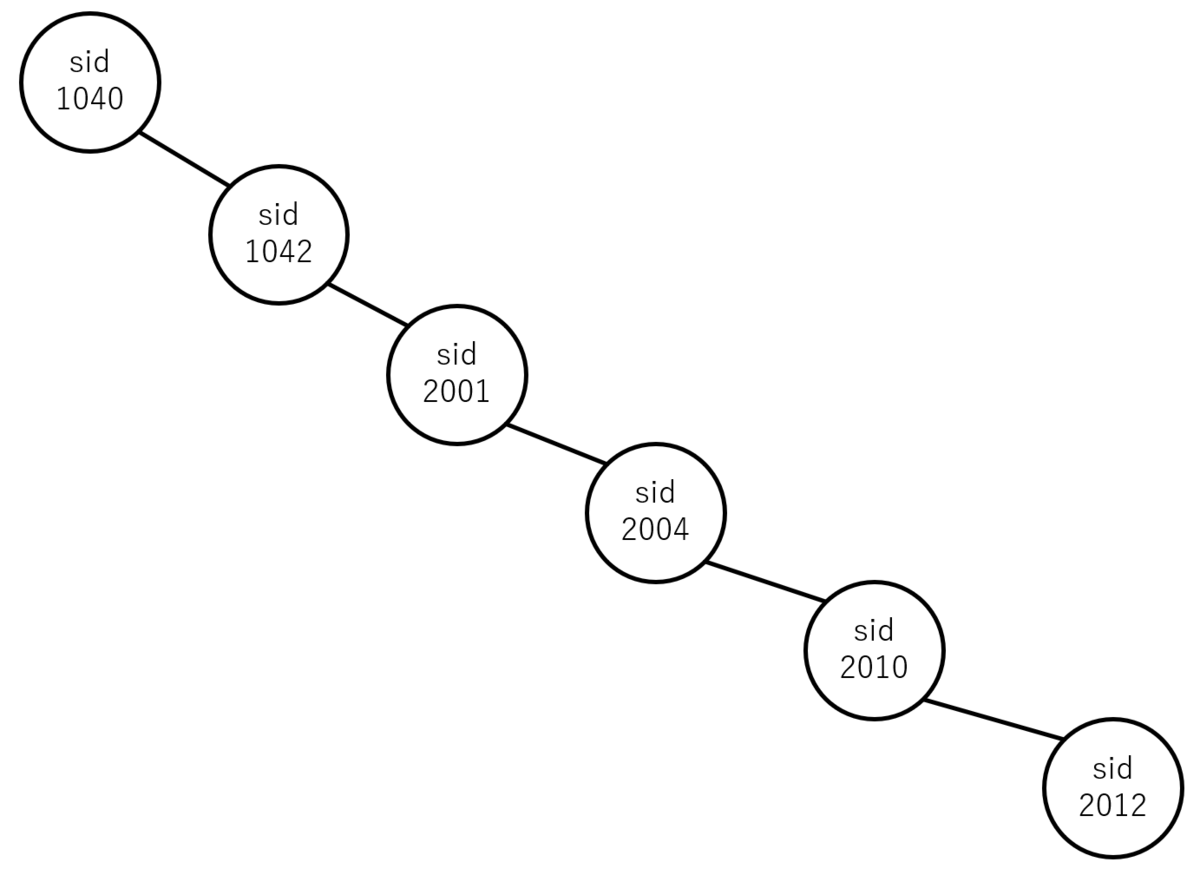
(2-ii)

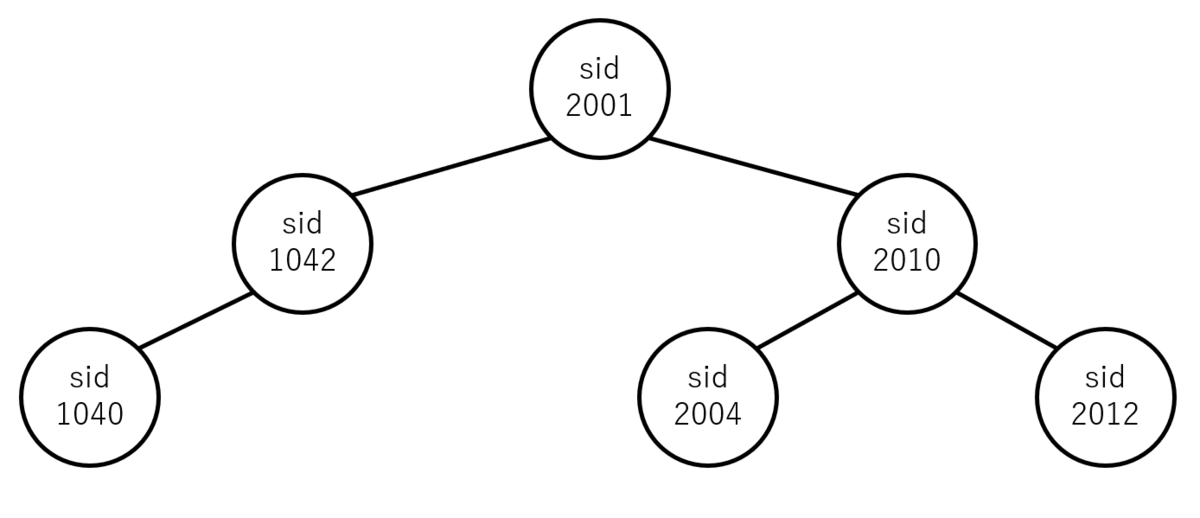
(3)

解答は分かりやすいよう空欄だけでなく周りごと書いてある。

// D, E
if (root->left != NULL) {
  enumerate(root->left);
}
// F, G
if (root->right != NULL) {
  enumerate(root->right);
}

(4)

\(0\) 個の場合、そのノードをただ消せばよい。

\(1\) 個の場合、そのノードを消すと同時にその子ノードをそのノードがあった場所に引き上げる。

\(2\) 個の場合、そのノードを消すと同時に、右部分木の最小ノードを外して、そのノードがあった場所へと移動する。 この最小ノードをはずす際はノードを削除する手順を再帰的に適用する。

(5)

同じ sid を持つノードは追加されない。 問題点は一つの sid を複数個保持することはできない。

(6)

要素数を \(n\) とすると、 利点は要素の探索にかかる平均計算量が \(O(n)\) の配列に比べて \(2\) 分探索木は \(O(\log n)\) と短いことで、 欠点は要素の追加にかかる平均計算量が \(O(1)\) の配列に比べて \(2\) 分探索木は \(O(\log n)\) と長いことである。