Skip to content

東京大学 工学系研究科 電気系工学専攻 2021年度 問題4 情報工学II

Author

donguri0912

Description

I.

論理回路に関する以下の問に答えよ．\(2\)bit の正の値 \(A = a_2a_1\) と \(B = b_2b_1\) を⼊⼒とする \(2\)bit⽐較器 \(\text{CMP}\) を設計したい．⽐較器 \(\text{CMP}\) は，⼊⼒が \(A \ge B\) の時 \(1\) を,それ以外の時 \(0\) を出⼒ \(c\) として出⼒する回路とする．\(2\)bit⽐較器 \(\text{CMP}\) は，図 \(1\) に⽰す記号で表される．

(1) \(a_1\), \(b_1\) を⼊⼒として，以下に⽰す \(c_1\) を出⼒する \(1\)bit⽐較器 \(\text{CMP}_1\) の真理値表を書け．

\[ c_1 = \left \{ \begin{aligned} 1,\quad a_1 \ge b_1 \\ 0,\quad a_1 < b_1 \\ \end{aligned} \right. \]

(2) 問 (1) に⽰した \(c_1\) と \(a_2\), \(b_2\) , を⼊⼒として，以下に⽰す \(c_2\) を出⼒する \(1\)bit⽐較器 \(\text{CMP}_2\) の真理値表を書け．

\[ c_2 = \left \{ \begin{aligned} &1,\quad a_2 > b_2 \\ &c_1,\quad a_2 = b_2 \\ &0,\quad a_2 < b_2 \\ \end{aligned} \right. \]

(3) 問 (1) および (2) で⽰した⽐較器 \(\text{CMP}_1 , \text{CMP}_2\) の回路を組合せることで \(2\)bit ⽐較器 \(\text{CMP}\) を作成することができる. この回路を図 \(2\) に⽰す記号を⽤いて図⽰せよ．

次に，\(2\)bit⽐較器 \(\text{CMP}\) を⽤いて順序回路 \(\text{MAX}\) を設計したい．\(\text{MAX}\) は，\(2\)bit の正の値 \(X_1\), \(X_2\), \(\cdots\) を順に⼊⼒すると，⼊⼒値の最⼤値を出⼒する．以下の⼿順で \(\text{MAX}\) の回路を設計せよ．

(4) \(2\)bit⽐較器 \(\text{CMP} と \(2\)bitの \(\text{D}\) フリップフロップ \(\text{(D-FF)}\) を⽤いて，\)\text{D-FF}$ に \(\max(A,B)\) を記録する回路を設計したい．この回路を図 \(1\) ，図 \(2\) および 図 \(3\) の記号を⽤いて図⽰せよ．

(5) 問 (4) で設計した回路の⼊⼒ \(A\) に \(X_i\) を, \(B\) に \(\max(X_1,X_2,\dots,X_{i-1})\) を配線することで，順序回路 \(\text{MAX}\) を作成できる．順序回路 \(\text{MAX}\) を図 \(1\) ，図 \(2\) および図 \(3\) の記号を⽤いて図⽰せよ．ここで，⼊⼒ \(B\) の初期値は \(00\) であると仮定してよい．

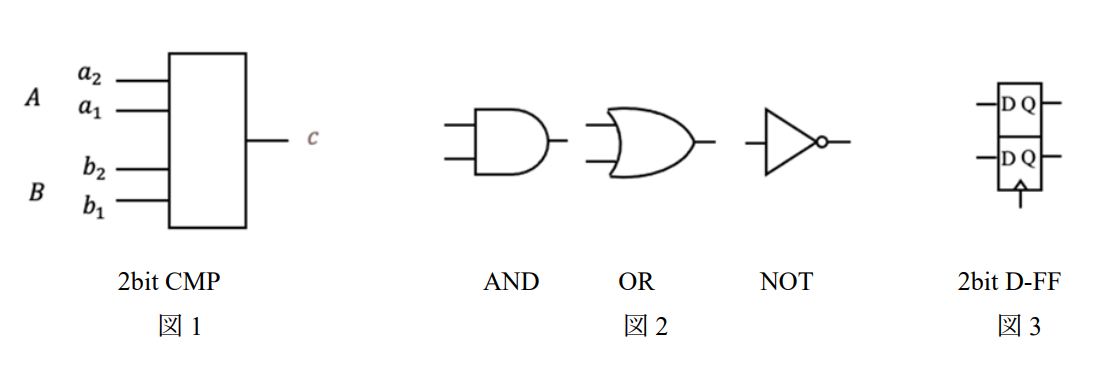
II.

ハッシュテーブルを⽤いたデータの格納と管理に関する以下の問に答えよ．\(N\) 個の要素を持つハッシュテーブル table[N]により正の整数を管理する⽅法について考える．ここで，正の整数 \(x\) をハッシュテーブルに格納する位置を定める際に⽤いるハッシュ関数を \(H(x) = mod(x,N)\) とする．正の整数が同じハッシュ値を持つ場合は，プログラム 1に⽰すデータ構造 nodeの連結リストにより管理する．

(1) 整数 \(\{15, 53, 22, 59, 15, 41, 20\}\) をハッシュ関数を⽤いて順に \(N = 11\) の table[N]に格納した時，ハッシュテーブルの内容を⽰せ．

(2) プログラム 2 は，正の整数 \(x\) をtable[N] に格納する関数 insert(x) を⽰している．プログラム 2 の空欄を埋めて \(\text{C}\) ⾔語のプログラムを完成させよ．

(3) search(x) は，与えられた正の整数 \(x\) の値が table[N] に格納されている場合に \(1\) を, そうでない場合は \(0\) を返す関数とする．関数 search(x) を \(\text{C}\) ⾔語で記述せよ．

(4) table[N] に格納されている正の整数 \(x\) を削除する関数を記述する際に留意すべき点を数⾏で述べよ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
/* プログラム 1 */ 
struct node {
    int  value; 
    struct node *next;
}; 
struct node *table[N];

/* プログラム 2 */ 
int H(int x) { return(x % N); } void insert(int x) {
    struct node *new, *check; new = (struct node *)malloc(sizeof (struct node)); new -> value = x; new -> next = NULL; check = table[H(x)]; 
    /* ------------------------------------------- */
    /* |                                         | */
    /* |                 BLANK                   | */
    /* |                                         | */
    /* ------------------------------------------- */
}

Kai

I.

(1)

\(a_1\) \(b_1\) \(c_1\)
0 0 1
0 1 0
1 0 1
1 1 1

(2)

\(c_1\) \(a_2\) \(b_2\) \(c_2\)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1

(3)

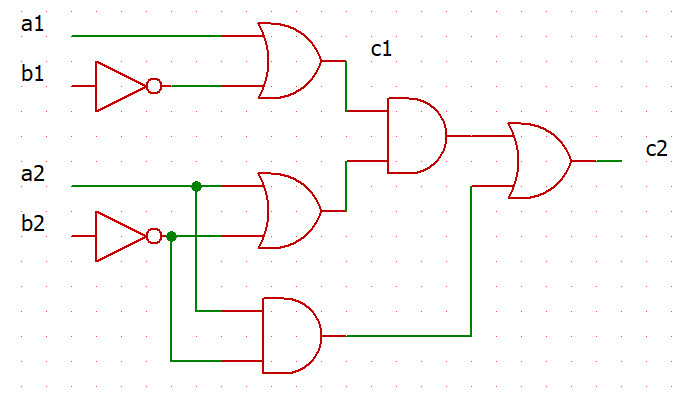
PCで書くのが面倒だったので載せませんがカルノー図を書きます。

(4)

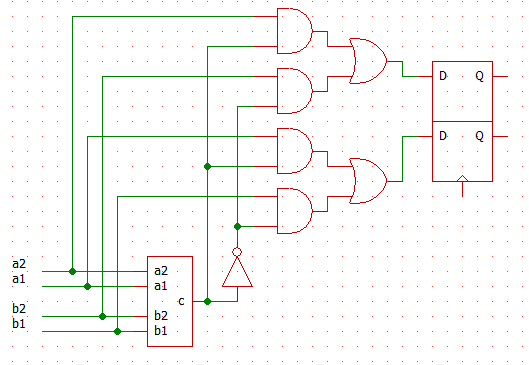
(5)

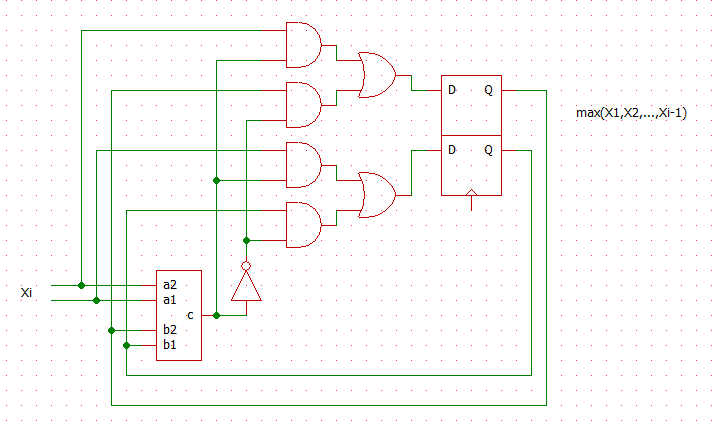
II.

(1)

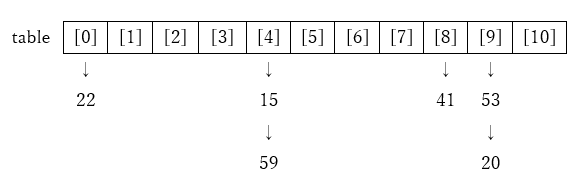
ハッシュテーブルに一般的な書き方があるわけではないと思うので、書き方はなんでもいいと思う。

(2)

1
2
3
4
5
6
if(check == NULL) {
  table[H(x)] = new;
} else {
  while(check->next != NULL) check = check->next;
  check->next = new;
}

(3)

1
2
3
4
5
6
7
8
int search(int x) {
  struct node *check = table[H(x)];
  while(check != NULL) {
    if(check->value == x) return 1;
    check = check->next;
  }
  return 0;
}

(4)

\(x\) を格納するノードを消す際にその子ノードを消さずに親につなげること。 また、\(x\) を格納するノードのメモリを開放すること。