Skip to content

東京大学 工学系研究科 電気系工学専攻 2020年度 問題4 情報工学II

Author

donguri0912

Description

I.

Answer the following questions on sequential circuits. We consider a circuit that has four states \(S=\{s0, s1, s2, s3\}\). The circuit changes its state and output \(Y\) according to the value of input \(X\). Table \(1\) shows the state transition table of the circuit.

(1) Draw the state transition diagram that is equivalent to the state transition table in Table \(1\).

(2) Show the shortest input sequence that outputs \(Y=1\) when the initial state is \(s2\).

Next, assume that we represent the state S with two bits as \(s0=00\), \(s1=01\), \(s2=10\), \(s3=11\). We consider designing the circuit with two JK-Flip Flop (JK-FF) \(F_A\) and \(F_B\).We represent the higher bit of the states with \(Q_A\), and the lower bit with \(Q_B\) such as \(s=Q_AQ_B\). \(F_A\) and \(F_B\) hold the states \(Q_A\) and \(Q_B\) in the circuits, respectively. A JK-FF has one bit state Q, and the state transits as shown in Fig. \(1\) according to inputs J and K.

(3) Copy Table \(1\) to your answer sheet and complete the table by filling the blanks. Here, (\(J_A, K_A\)) and (\(J_B, K_B\)) are the inputs to \(F_A\) and \(F_B\), respectively. Use \(d\) for "don't care" conditions.

(4) Simplify the input functions of \(J_A, K_A, J_B, K_B\) and output function of \(Y\) by using Karnaugh maps.

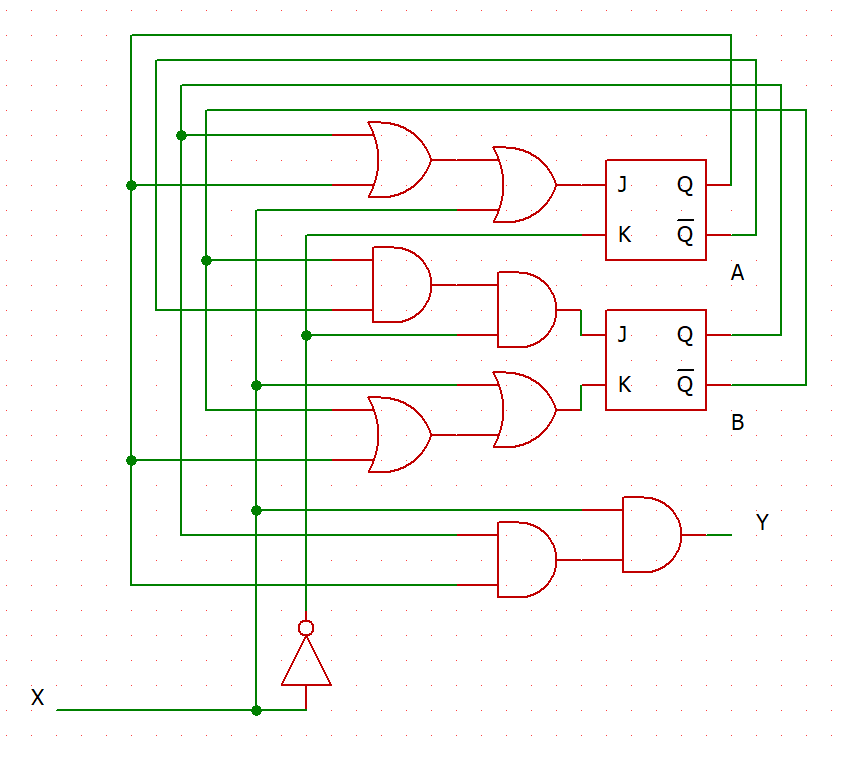
(5) Draw the circuit using the symbols shown in Fig. \(2\).

Table 1
Current state \(S(t)\) Input \(X\) Next state \(S(t+1)\) Output \(Y\) \(Q_A(t)\) \(Q_B(t)\) \(Q_A(t + 1)\) \(Q_B(t + 1)\) J_A K_A J_B K_B
\(s_0\) 0 \(s_1\) 0
\(s_0\) 1 \(s_2\) 0
\(s_1\) 0 \(s_3\) 0
\(s_1\) 1 \(s_2\) 0
\(s_2\) 0 \(s_0\) 0
\(s_2\) 1 \(s_2\) 0
\(s_3\) 0 \(s_0\) 0
\(s_3\) 1 \(s_2\) 1

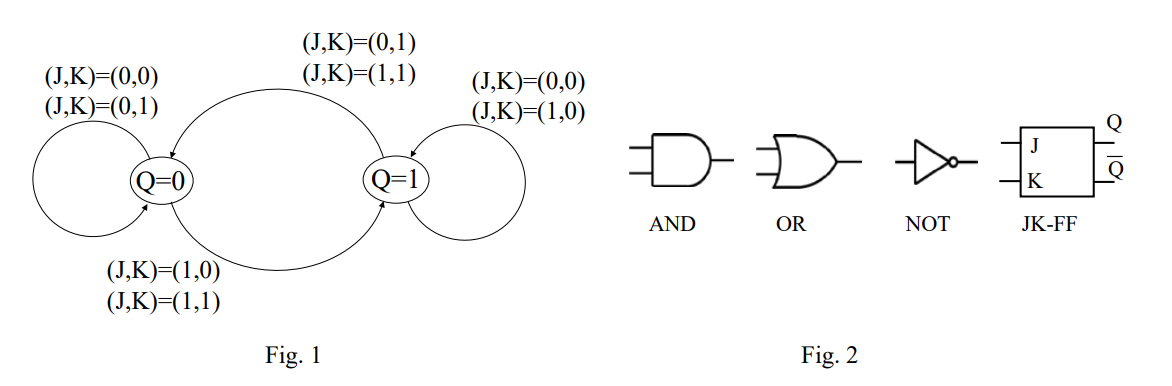
II.

Answer the following questions on heapsort. Assume that max heap is an array representation of a binary tree where the value in a parent node is greater than the values in its two children nodes. The structure of the array is as follows: assuming that the index \(i\)is an integer greater than or equal to \(1\), the value in the left child node of node \(i\) is stored in the \((i \times 2)\)-th element of the array, and the value in the right child node of node \(i\) is stored in the \((i \times 2 + 1)\)-th element of the array.

The function make_heap in Program \(1\) is a function that generates the max heap from an array with n items.The first element of the array is stored in array[1].The function swap(array,i,j) in Program \(1\) is a function that switches the values of array[i] and array[j].Here,the values in the array are integers,and there is no duplication among them.

(1) Assume that the number of items is \(7 (n=7)\), and the input array stores the values \(\{1, 7, 8, 9, 6, 4, 5\}\) in this order. Find the max heap that is generated by make_heap in Program \(1\).

(2) Draw the process of generating the max heap in Question (1) with binary trees. The arrays follow the same structure as the max heap even during the process of making max heap. You do not need to draw the trees that remain unmodified in the process.

(3) Give the order of the time complexity of make_heap according to the number of comparisons of the values.

Assume that we sort a max heap by iteratively taking the maximum value and rebuilding a max heap with the remaining items.

(4) Describe a function by using the \(C\) programming language in as few lines as possible to sort a max heap array with n items in descending order. Use the function make_heap in Program \(1\) for rebuilding the max heap in your function.

(5) Describe an overview of an algorithm to sort an array using max heap, which is more computationally efficient than that obtained in Question (4). The sort order can be either ascending order or descending order. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
/* Program 1 */ 
void push_down(int array[], int n, int node) {     
    if(node * 2 > n)    return;     
    int     parent = node, child;     
    do {         
        child = parent * 2;
        if ((child < n) && (array[child] < array[child + 1]))             
            child = child + 1;         
        if (array[child] < array[parent])
            break; 
        swap(array, child, parent);
        parent = child;
    }while (parent * 2 <= n); 
} 

1
2
3
4
5
void make_heap(int array[], int n){
    int    node;
    for (node = n / 2; node >= 1; --node)
        push_down(array, n, node);
}

Kai

I.

(1)

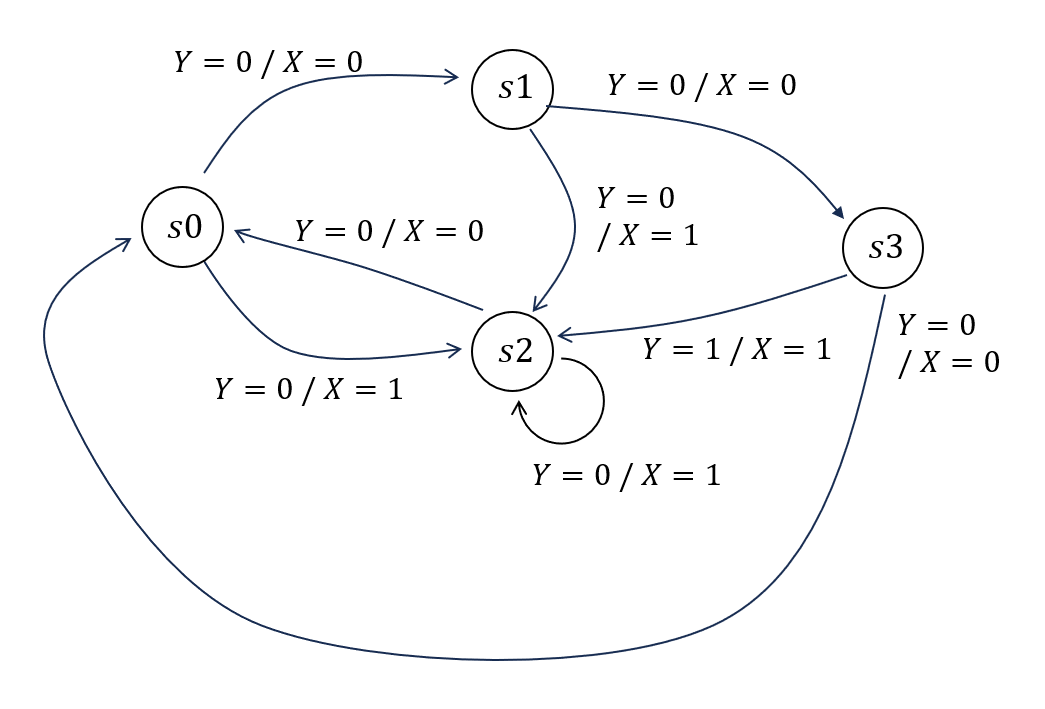
(2)

\(x = 0,0,0,1\) の順

(3)

Current state \(S(t)\) Input \(X\) Next state \(S(t+1)\) Output \(Y\) \(Q_A(t)\) \(Q_B(t)\) \(Q_A(t + 1)\) \(Q_B(t + 1)\) J_A K_A J_B K_B
\(s_0\) 0 \(s_1\) 0 0 0 0 1 0 \(d\) 1 \(d\)
\(s_0\) 1 \(s_2\) 0 0 0 1 0 1 \(d\) 0 \(d\)
\(s_1\) 0 \(s_3\) 0 0 1 1 1 1 \(d\) \(d\) 0
\(s_1\) 1 \(s_2\) 0 0 1 1 0 1 \(d\) \(d\) 1
\(s_2\) 0 \(s_0\) 0 1 0 0 0 \(d\) 1 0 \(d\)
\(s_2\) 1 \(s_2\) 0 1 0 1 0 \(d\) 0 0 \(d\)
\(s_3\) 0 \(s_0\) 0 1 1 0 0 \(d\) 1 \(d\) 1
\(s_3\) 1 \(s_2\) 1 1 1 1 0 \(d\) 0 \(d\) 1

(4)

(5)

II.

(1)

\(\{9,7,8,1,6,4,5\}\)

問題のコードはC言語と違って配列のインデックスが1スタートなので注意。

(2)

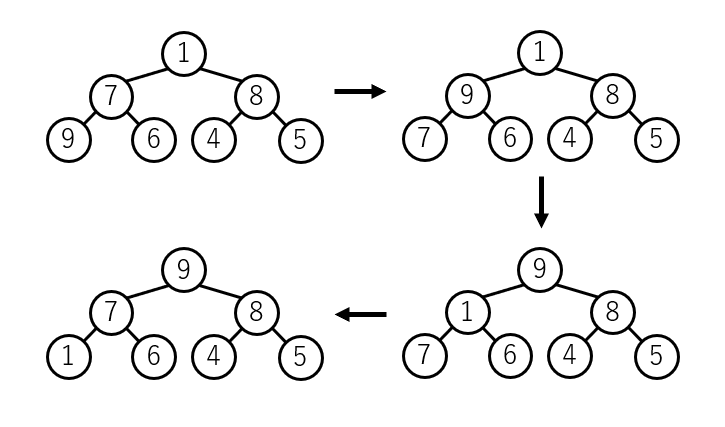
(3)

要素の数を \(n\) として、\(O(n \log n)\)

(4)

本解: 

1
void sort_by_heap(int array[], int n) { for(int i = 0; i < n - 1; i++) make_heap(array + i, n - i); }

本解を改行したもの: 

1
2
3
void sort_by_heap(int array[], int n) {
  for(int i = 0; i < n - 1; i++) make_heap(array + i, n - i);
}

参考解: 

1
2
3
4
5
6
7
void sort_by_heap(int array[], int n) {
  for(int i = n; i > 1; i--) {
    make_heap(array, i);
    swap(array, 1, i);
  }
  for (int i =1; i <= n / 2; i++) swap(array, i, n - i + 1);
}

ヒープソートの話かなと思ったので最初参考解を思いついたが、as few lines as possibleという問題文の指示が気になったので本解の方を思いついた。もっとも、どんなプログラムであれ改行無しで書けば \(1\) 行になるのだが。 どちらもmake_heapを実行するとarrayの先頭が最大値になることを利用している。以下は本解の解説。

make_heapの引数は先頭アドレスarray + i、サイズn - iの配列を渡すという意味である。本来先頭アドレスarray、サイズnの配列から部分配列を切り出してmake_heapに渡す操作を行っている。ちなみに配列はメモリ上で、(インデックスが \(1\) スタートのこのプログラムにのっとって言うと、)アドレスarrayにarray[1]、array + 1にarray[2]、...、array + n - 1にarray[n]という風に配置されている。

for文の()の中の書き方のコツはイテレータ変数(解答でいうとi)の初期値と最終値だけ見ることである。今回は初期値がi = 0で、条件式i < n - 1がi = n - 2の時まではtrueになることから最終値がi = n - 2になることがわかる。make_heapに渡した引数の方も初期値と最終値だけ考えればよく、初期値が(array, n)、最終値が(array + n - 2, 2)であることがわかる。別にi = n - 1まで回してもいいのだが、その時はサイズ \(1\) の配列をmake_heapすることになり何も起こらないので条件式をi < n - 1に設定している。ちなみにi <= n - 2としてもよい。こちらの方が直感的かもしれない.

(5)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
array をサイズ n の int 型配列とする。
1. まず、make_heap を用いて array に max heap を作る。
次に、array の先頭 array[1] は max heap 中の最大値となっているので、
それを array の最後の要素 array[n] と swap する。

2. n2 = n-1, n-2, ..., 2 に対して下記を実行する。
先頭アドレス array[1]、サイズ n2 の array の部分配列を array2 と定義する。
array2 は array2[1] の要素以外は max heap の条件を満たしている。
array2[1] も max heap の条件を満たすため、
push_down(array2, n2, 1) (つまり push_down(array, n2, 1))を実行し、
木の下方に向かって並べ替える。
その後、array2[1] はまた max heap 中の最大値となっているのでarray2[n2] と swap する。

以上の手順により並べ替えられた array は先頭から昇順に並んでいる。

仰々しく書いてしまったが要はヒープソートをやっている。コードで書くと次のよう。

1
2
3
4
5
6
7
8
void heap_sort(int array[], int n) {
  make_heap(array, n);
  swap(array, 1, n);
  for(int n2 = n - 1; n2 >= 2; n2--) {
    push_down(array, n2, 1);
    swap(array, 1, n2);
  }
}

計算量オーダーは (4) が \(O(n^2 \log n)\)、(5) が \(O(n \log n)\) なので (5) の方が効率的になっている。