東京大学 工学系研究科 電気系工学専攻 2020年度 問題3 情報工学I

Author

donguri0912

Description

I

Answer the following questions on information theory. Suppose that we transmit information by using a time-discrete communication channel \(C\), whose input and output are designated as \(X \in \{-1,1\}\) and \(Y \in \{-1,1\}\), respectively. The input and output relation of the \(i\)-th communication via \(C\) is represented as \(Y_i = Z_i \times X_i(i = 1,2,\cdots)\), where \(\times\) means the multiplication of integers. \(Z_i \in \{-1,1\}\) is an internal state of the channel at the \(i\)-th communication, and its value can change depending on the current or past states of the input and on the past states of the output. Both sender and receiver are unable to observe the value of \(Z_i\) directly although they can have knowledge about how \(Z_i\) changes depending on the input and output. Use the logarithm base \(2\) for your answers of the following questions. You may also use the following approximations upon necessity: \(\log_23 = 1.585\), \(\log_25 = 2.322\), \(\log_27 = 2.807\).

(1) Let \(X_i\) be an ideally independent random variable that takes \(X_i = 1\) with probability \(\mu\) and \(X_i = -1\) with probability \(1 - \mu\). Assume that \(Z_i\) becomes \(1\) with probability \(1\) when \(X_i = 1\) and that it takes either \(1\) or \(-1\) with equal probability when \(X_i = -1\).

• (1-i) Obtain the entropies \(H[X]\) and \(H[Y]\) and the conditional entropy \(H[Y|X]\) of \(C\).
• (1-ii) Obtain the channel capacity of \(C\).

(2) Assume that \(Z_1\) takes either \(1\) or \(-1\) with equal probability and that, for \(i \ge 2\), the value of \(Z_i\) becomes the same as the previous output value \(Y_{i-1}\) with probability \(1\) as \(Z_i = Y_{i-1}\).Obtain the maximum bits that can be transmitted by using this channel \(n\) times.

(3) Assume that \(Z_1\) takes either \(1\) or \(-1\) with equal probability when \(i\) is odd and that \(Z_i\) keeps its previous value with probability \(1\) as \(Z_i = Z_{i-1}\) when \(i\) is even.Obtain the channel capacity of \(C\) and show a code that can achieve the capacity.

(4) Assume that \(Z_1 = 1\) with probability \(1\) and that, for \(i \ge 2\), the value of \(Z_i\) becomes the same as the previous input value \(X_{i-1}\) with probability \(1\) as \(Z_i = X_{i-1}\). Let \(X_i\) be an ideally independent random variable that takes \(X_i = 1\) with probability \(\mu\) and \(X_i = -1\) with probability \(1 - \mu\).Calculate the probability \(q\) that \(Y_i = 1\) at the stationary state for sufficiently large \(i\).

II

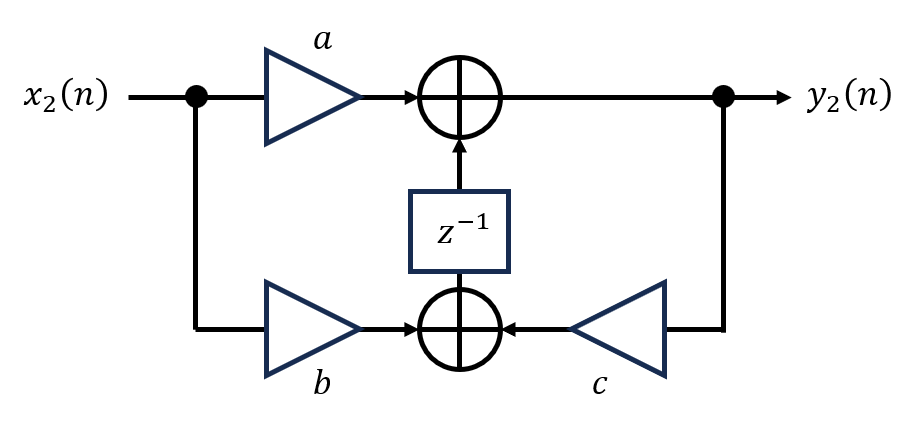
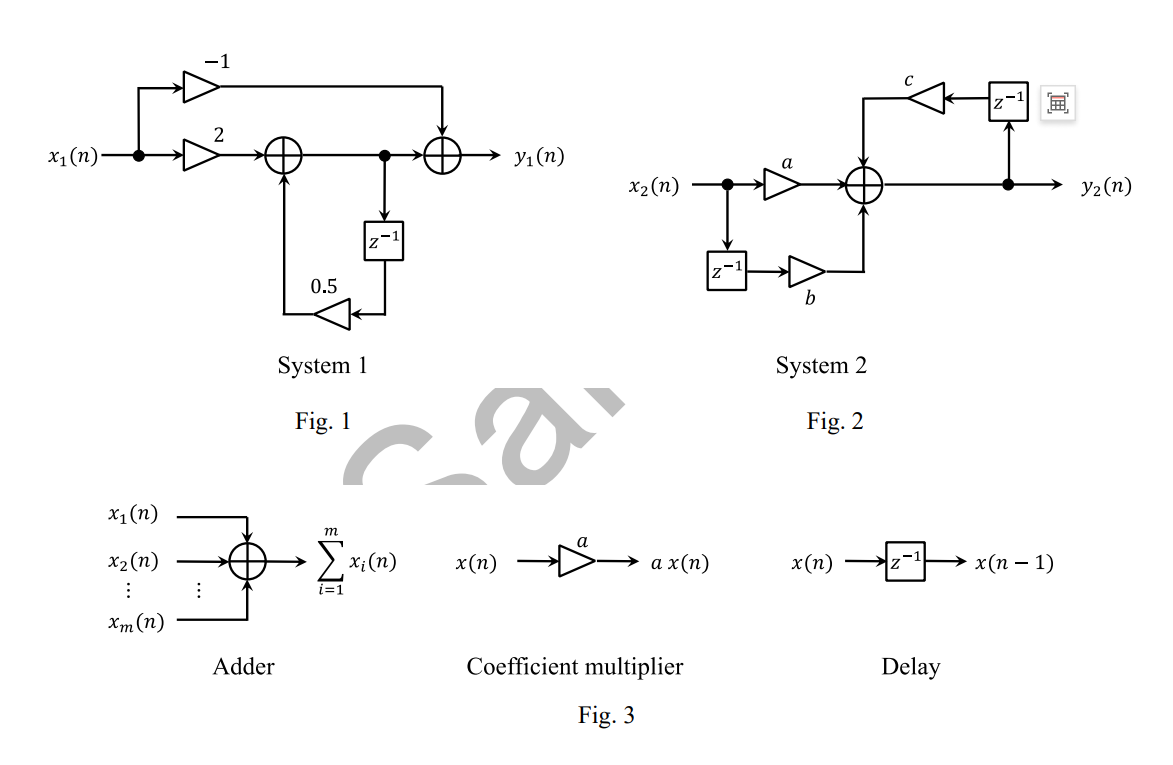
Answer the following questions on signal processing. Consider the two infinite impulse response systems shown in Figs. \(1\) and \(2\). \(x_1(n)\) and \(y_1(n)\) are the input and output signal sequences of system \(1\) in Fig. \(1\), respectively, and represent the signal values at time \(nT(T > 0)\) for \(n = 0,1,\cdots\).Similarly, \(x_2(n)\) and \(y_2(n)\) are the input and output sequences of system \(2\) in Fig. \(2\). The circuits consist of adders, coefficient multipliers, and delays, whose respective functions are described in Fig. \(3\).

(1) Obtain the impulse response of system \(1\), \(h_1(n)\), and its \(z\)-transform \(H_1(z)\).

(2) Calculate the frequency response of system 1 and explain the filtering function of this system on the input signal.

(3) Obtain the parameter values of \(a,b\) and \(c\) that makes system \(2\) equivalent to system \(1\).

(4) Draw an equivalent circuit of system \(2\) that has a smaller number of delays than the original system \(2\) shown in Fig. \(2\).

Kai

I

(1)

\(\mathcal{H}(\cdot)\) はエントロピー関数

(1-i)

\[ H[X] = \mathcal{H}(\mu) = -\mu\log\mu - (1 - \mu)\log(1 - \mu) \]

\[ \begin{aligned} H[Y] &= \mathcal{H}(0.5(1 - \mu)) \\ &= -0.5(1 - \mu)\log0.5(1 - \mu) - 0.5(1 + \mu)\log0.5(1 + \mu) \\ &= -0.5(1 - \mu)\log(1 - \mu) - 0.5(1 + \mu)\log(1 + \mu) - 0.5(1 - \mu)\log0.5 - 0.5(1 + \mu)\log0.5 \\ &= -0.5(1 - \mu)\log(1 - \mu) - 0.5(1 + \mu)\log(1 + \mu) + 1 \\ \end{aligned} \]

\[ H[Y|X] = \mu\mathcal{H}(1) + (1 - \mu)\mathcal{H}(0.5) = 1 - \mu \]

(1-ii)

\[ \begin{aligned} &I(X;Y) = H[Y] - H[Y|X] \\ &= -0.5(1 - \mu)\log(1 - \mu) - 0.5(1 + \mu)\log(1 + \mu) + 1 - (1 - \mu) \\ &= -0.5(1 - \mu)\log(1 - \mu) - 0.5(1 + \mu)\log(1 + \mu) + \mu \end{aligned} \]

\[ \begin{aligned} \frac{dC_c}{d\mu} &= 0.5\log(1 - \mu) + \frac{0.5}{\log_e2} - 0.5\log(1 + \mu) - \frac{0.5}{\log_e2} + 1 \\ &= 0.5\log\frac{1 - \mu}{1 + \mu} + 1 = 0 \end{aligned} \]

となる時、つまり \(\mu = \frac{3}{5}\) で最小となる。

このとき

\[ \begin{aligned} I(X;Y)|_{\mu = \frac{3}{5}} &= -0.5\frac{2}{5}\log\frac{2}{5} - 0.5\frac{8}{5}\log\frac{8}{5} + \frac{3}{5} \\ &= -\frac{1}{5}\log2 - \frac{4}{5}\log8 + \log5 + \frac{3}{5} \\ &= 0.322 \end{aligned} \]

よって、求める通信路容量 \(C_C = \max_{\mu}I(X;Y) = 0.322\)

(2)

\(n\) 回目に送信できる最大のビットは \(n\) 回目の通信路容量 \(C_n\) に等しく、\(n\) 回目の通信路はそれぞれ \(2\) 元対称通信路として考えられることから \(C_n = \max I(X;Y) = \max(H[Y]) - H[Y|X]\) と計算できる。

\(n = 1\) のとき、\(n - 1\) 回目の \(Y\) が分かっているので、\(C_n = 1 - \mathcal{H}(1) = 1\) よって、\(n\) 回で遅れるビット数は \(n - 1\) ビットである。

(3)

通信路は \(2\) 元対称通信路として考えられることから、奇数回目の時、

\[ C_{\text{奇数回目}} = \max I(X;Y) = \max(H[Y]) - H[Y|X] = 1 - \mathcal{H}(0.5) = 0 \]

偶数回目の時、前回の \(Z\) が分かっていれば、符号は連続した奇数回目と偶数回目を一つの符号として、\(1\ 1、1\ -1\) を符号語にし、復号領域としてそれぞれ \(\{1\ 1,-1-1\}\)、\(\{1-1,-1\ 1\}\) を設ければよい。

(4)

\(i\) が十分大きい場合について、\(X_i\), \(X_{i-1}(=Z_i)\) は独立な確率変数である。よって、\(Y_i = 1\) となる確率 \(q\) は

\[ q = \mu^2 + (1 - \mu)^2 = 2\mu^2 - 2\mu + 1 \]

II

(1)

\(x_1(n)\)、\(x_2(n)\) の \(z\) 変換を \(X_1(z)、Y_1(z)\) となる。

\[ \begin{aligned} &Y_1(z) = \frac{1}{1 - 0.5z^{-1}} \times 2X_1(z) - X_1(z) \\ &H_1(z) = \frac{Y_1(z)}{X_1(z)} = \frac{2}{1 - 0.5z^{-1}} - 1\\ &h_1(n) = \delta(n) + 2 \times 0.5^n \end{aligned} \]

\(2 \times 0.5^n\) は \(u(n)\) をつけても良い。

(2)

\[ H_1(z) = \frac{2}{1 - 0.5z^{-1}} - 1 = \frac{1 + 0.5z^{-1}}{1 - 0.5z^{-1}} \]

ゼロ点は \(z = 2e^{\pm j\pi}\)、極は \(z = 2e^0\) である。 よって高周波をカットするローパスフィルタである。

(3)

\(x_2(n)\)、\(y_2(n)\) の \(z\) 変換を \(X_2(z)\)、\(Y_2(z)\) とする。

\[ \begin{aligned} &Y_2(z) = aX_2(z) + bz^{-1}X_2(z) + cz^{-1}Y_2(z) \\ &(1 - cz^{-1})Y_2(z) = (a + bz^{-1})X_2(z) \\ &\frac{Y_2(z)}{X_2(z)} = \frac{a +_ bz^{-1}}{1 - cz^{-1}} \end{aligned} \]

これが \(H_1(z)\) と一致するとき、\(a = 1\)、\(b = 0.5\)、\(c = 0.5\)。

(4)