東京大学 情報理工学研究科 数理情報学 2023年度 第1問
Author
hari64boli64
Description
正の整数 \(m, n\) および有限実数数列 \(A = \{a_i\}_{i=1}^m, B = \{b_j\}_{j=1}^n\) に対して、
\[
f(A,B)=\ln{\left(
\frac{1}{m}\sum_{i=1}^{m}{
\frac{1}{\frac{1}{n}\sum_{j=1}^{n}{e^{-|a_i-b_j|}}}}
\right)}
\]
と定義する。ただし、\(\ln\) は自然対数を表す。以下の設問に答えよ。
(1) \(f(A, B) \ge 0\) が成り立つことを示せ。また、\(f(A, B) = 0\) となる \(A, B\) の必要十分条件を求めよ。
(2) 任意の空でない有限実数数列 \(A, B, C\) に対して、
\[
f(A, C) \leq f(A, B) + f(B, C)
\]
が成り立つことを示せ。
(3) 任意の実数 \(s\) に対して、\(A_m(s) = \{s + \frac{i}{m}\}_{i=1}^m, B_n = \{\frac{j}{n}\}_{j=1}^n\) とおき、\(g(s)\) を
\[
g(s) = \lim_{m \to \infty} \lim_{n \to \infty} f(A_m(s), B_n)
\]
で定める。このとき、
\[
g(s) = \ln \left( \int_s^{1+s} \frac{1}{h(z)} dz \right)
\]
となるような関数 \(h(z)\) の具体的な表式を導出せよ。
(4) \(g(s)\) が最小となる実数 \(s\) を求めよ。
Kai
(1)
\[
\begin{aligned}
& -|a_i-b_j| \leq 0 \\
\Rightarrow & \frac{1}{n}\sum_{j=1}^{n}{\exp(-|a_i-b_j|)} \leq 1 \\
\Rightarrow & \frac{1}{m}\sum_{i=1}^{m}{\frac{1}{\frac{1}{n}\sum_{j=1}^{n}{\exp(-|a_i-b_j|)}}} \geq 1 \\
\Rightarrow & f(A,B) \geq 0
\end{aligned}
\]
等号成立条件は、上の式変形より、\(\forall \; i,j, \; a_i=b_j\) である。
(2)
定義に従って示せばよい(変則的だが、分かりやすさの為、左向きの矢印を使用する)。
\[
\begin{aligned}
& f(A,C) \leq f(A,B)+f(B,C) \\
\Leftarrow & \frac{1}{m}\sum_{i=1}^{m}{\frac{1}{\frac{1}{l}\sum_{k=1}^{l}\exp(-|a_i-c_k|)}} \leq \Big(\frac{1}{m}\sum_{i=1}^{m}{\frac{1}{\frac{1}{n}\sum_{j=1}^{n}\exp(-|a_i-b_j|)}}\Big) \Big(\frac{1}{n}\sum_{j=1}^{n}{\frac{1}{\frac{1}{l}\sum_{k=1}^{l}\exp(-|b_j-c_k|)}}\Big) \\
\Leftarrow & \sum_{k=1}^{l}\exp(-|a_i-c_k|) \geq \frac{\sum_{j=1}^{n}\exp(-|a_i-b_j|)}{\sum_{j=1}^{n}{\frac{1}{\sum_{k=1}^{l}\exp(-|b_j-c_k|)}}} \\
\Leftarrow & \sum_{j=1}^{n}{\frac{\sum_{k=1}^{l}\exp(-|a_i-c_k|)}{\sum_{k=1}^{l}\exp(-|b_j-c_k|)}} \geq \sum_{j=1}^{n}\exp(-|a_i-b_j|) \\
\Leftarrow & \sum_{k=1}^{l}\exp(-|a_i-c_k|) \geq \exp(-|a_i-b_j|)\Big(\sum_{k=1}^{l}\exp(-|b_j-c_k|)\Big) \\
\Leftarrow & \exp(-|a_i-c_k|) \geq \exp(-|a_i-b_j|)\exp(-|b_j-c_k|) \\
\Leftarrow & |a_i-c_k| \leq |a_i-b_j|+|b_j-c_k|
\end{aligned}
\]
最後の不等式は、三角不等式より成立する。
以上より、\(f(A,C) \leq f(A,B)+f(B,C)\) が示された。
(3)
区分求積法そのままなので、
\[
\begin{aligned}
h(z)=\int_0^1{e^{-|z-x|}} \text{d}{x}
\end{aligned}
\]
である。
よって、
\[
\begin{aligned}
h(z)=
\begin{cases}
e^{-z}(e-1) \; (1 \leq z) \\
2-e^{-z}+e^{z-1} \; (0 < z < 1) \\
e^{z}(1-e^{-1}) \; (z \leq 0)
\end{cases}
\end{aligned}
\]
となる。
(4)
\(h(z)\) は \(1/2\) を中心とする対称関数であり、
微分などを計算すると、図 1 のようになる。
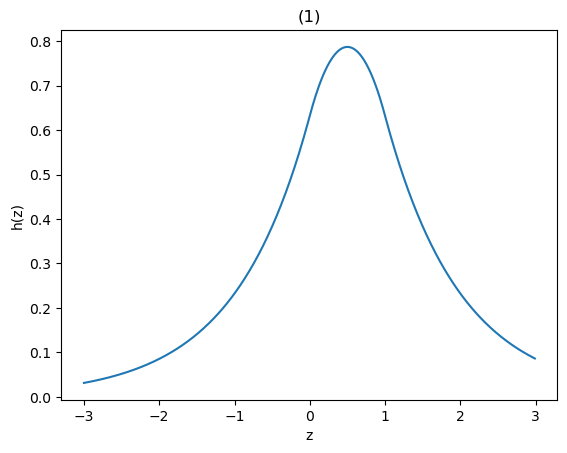
図1: \(h(z)\) のグラフ
よって、
あまり厳密な議論ではないが、
区間幅1の \(h(z)\) の最も大きな部分は \(s=0\) の時に成立する。
(しかし、これは厳密に行う事も出来るはず)
以上より、\(s=0\) が答え。
実際、これが正しいことは、図 2 より分かる。
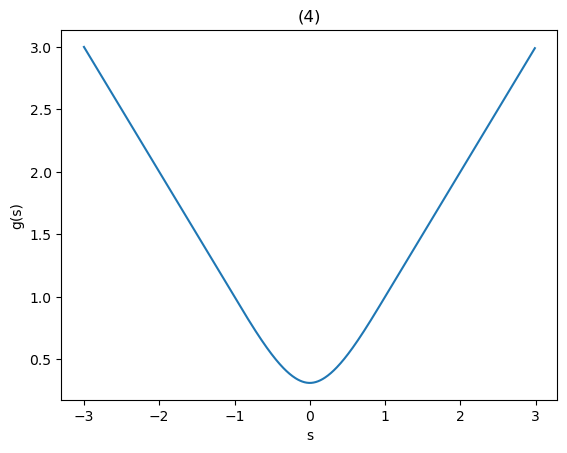
図2: \(g(s)\) のグラフ

