東京大学 情報理工学研究科 数理情報学 2020年度 第2問
Author
hari64boli64
Description
ある生物の生存時間は平均 \(\mu\) の指数分布に従う。
この生物 \(n\) 匹の生存時間を観測することで \(\mu\) を推定したい。
ただし実験上の制約により、生まれた直後の一定期間 \([0,a]\) は観測ができず、もしこの期間内に生物が死んだ場合には、死んだ事実だけが観測されるものとする。
\(a\) は正の定数である。
\(i = 1, \ldots, n\) に対し、第 \(i\) 番目の個体の生存時間を \(X_i\) とおく。
これらは平均 \(\mu\) の指数分布に従い、互いに独立とする。
平均 \(\mu\) の指数分布の確率密度関数は \(f(x; \mu) = (1/\mu)e^{-x/\mu} \ (x > 0)\) である。
また観測値 \(Y_i\) を
\[
Y_i =
\begin{cases}
a & (X_i \leq a \text{ のとき}) \\
X_i & (X_i > a \text{ のとき})
\end{cases}
\]
と定義する。
以下の問いに答えよ。
(1) \(Y_1\) の期待値を \(g(\mu)\) とおく。 \(g(\mu)\) を求めよ。
(2) \(\bar{Y} = n^{-1} \sum_{i=1}^n Y_i\) とおく。\(\bar{Y} > a\) のとき、 \(g(\hat{\mu}) = \bar{Y}\) を満たす \(\hat{\mu}\) がただ一つ存在することを示せ。
(3) \(Y_i = a\) を満たす \(i\) の個数を \(M\) とおく。\(0 \leq m \leq n - 1\) および \(b > a\) に対して
\[
P(M = m, \bar{Y} \leq b) = \int_a^b h(m, y; \mu) \text{d}y,
\]
を満たす関数 \(h(m, y; \mu)\) を求めよ。
(4) \(m < n\) かつ \(y > a\) のとき、 \(h(m, y; \mu)\) を最大にする \(\mu\) がただ一つ存在することを示せ。
Kai
(1)
\(Y_1\) の期待値は
\[
\begin{aligned}
\int_0^a af(x;\mu)\text{d}x + \int_a^\infty xf(x;\mu)\text{d}x=a+\mu e^{-\frac{a}{\mu}}
\end{aligned}
\]
(2)
\(g(\hat{\mu})-a=\hat{\mu}e^{-\frac{a}{\hat{\mu}}}\) を考える。
存在は、連続性と \(\lim_{x \to \infty}\hat{\mu}e^{-\frac{a}{\hat{\mu}}} \to \infty\) より明らか。
一意性は、微分すると狭義単調と分かるので明らか。
(3)
（自信なし。）
まず、\(P(M=m)\) を求める。
\(P(Y_1=a)=\int_0^a{f(x;\mu)}\text{d}x=1-e^{-\frac{a}{\mu}}\)より、\(P(M=m) = {}_NC_m (1-e^{-\frac{a}{\mu}})^m(e^{-\frac{a}{\mu}})^{N-m}\)
次に、\(P(\overline{Y}\leq b | M=m)\) を求める。
\[
\begin{aligned}
P(\overline{Y}\leq b | M=m) & = P\left( \sum_{i=1}^N Y_i \leq Nb \middle| M=m \right) \\
& = P\left( am + \sum_{i=1}^{N-m} (Y_i+a) \leq Nb \right) \\
& = P\left( \sum_{i=1}^{N-m} Y_i \leq N(b-a) \right) \\
& = \int_0^{N(b-a)} f_{N-m}(y) \text{d}y \\
& = \int_a^{b} Nf_{N-m}(N(y-a)) \text{d}y \\
\end{aligned}
\]
ただし、一行目から二行目の変形で、指数分布の無記憶性を用いた。
また、\(f_{N-m}\) で、指数分布を \(N-m\) 個重ね合わせた分布を示している。
これは、ガンマ分布に従うことが一般に知られている。(後述)
以上より、
\[
\begin{aligned}
P(M=m,\overline{Y}\leq b) & = P(M=m)P(\overline{Y} \leq b|M=m) \\
& = {}_NC_m (1-e^{-\frac{a}{\mu}})^m(e^{-\frac{a}{\mu}})^{N-m} \int_a^{b} N f_{N-m}(N(y-a)) \text{d}y \\
& = {}_NC_m (1-e^{-\frac{a}{\mu}})^m(e^{-\frac{a}{\mu}})^{N-m} \int_a^{b} \frac{N}{(N-m-1)!\mu^{N-m}} (N(y-a))^{N-m-1} e^{-\frac{Ny-a}{\mu}} \text{d}y \\
\end{aligned}
\]
(4)
\(\mu\) に関連する部分だけ取り出すと、
\[
\begin{aligned}
M(\mu) & = (1-e^{-\frac{a}{\mu}})^m(e^{-\frac{a}{\mu}})^{N-m} \frac{1}{\mu^{N-m}} e^{-\frac{N(y-a)}{\mu}}
\end{aligned}
\]
となるが、これを微分するのは大変な困難を伴うように思われる。
なので、別の方針を考える。
\[
\begin{aligned}
h(m,y;\mu) & =\frac{\text{d}}{\text{d}y} \left(\int_a^y{h(m,y';\mu)}\text{d}y' \right) \\
& =\frac{\text{d}}{\text{d}y} \left(P(M=m,\overline{Y}\leq y) \right) \\
& =P(M=m,\overline{Y}=y) \\
\end{aligned}
\]
ただし、最後の変形で、累積分布関数の微分が確率密度関数になることを用いた。
細かい議論は (2) などと同様になるので省くが、無記憶性を用いた議論や適切な変形を経ると、結局のところ、指数分布の確率密度関数 \(f(x;\mu)\) について、ある値 \(Y\) を取る確率が最大になるような \(\mu\) が、ただ一つ存在することを示す問題に帰着されると思われる。
(厳密にはガンマ分布に対して言うべきか?)
これは、(2) の議論とほぼ同様である。
以下では、おまけ程度に、上で示した問題の解を与える。
\[
\begin{aligned}
\frac{\partial}{\partial \mu} f(Y;\mu) & =-\frac{1}{\mu^2}e^{-\frac{Y}{\mu}}+\frac{1}{\mu}\frac{Y}{\mu^2}e^{-\frac{Y}{\mu}} \\
& =\frac{-mu+Y}{\mu^3}e^{-\frac{Y}{\mu}}
\end{aligned}
\]
よって、\(\frac{\partial}{\partial \mu} f(Y;\mu)=0\) となる \(\mu\) は、\(Y=\mu\) の時、これのみである。
以上で、大まかには題意が示された。
より詳細な議論を、本来は行うべきであろう。
Knowledge
指数分布は再生性を持たない。つまり、\(X_1,X_2,\cdots\) が独立に指数分布に従うとしても、\(X_1+X_2+\cdots\) は指数分布に従わない。
これは一般にはアーラン分布に従う。
特に、今回はガンマ分布に従う。これは以下の畳み込みの式と帰納法で示せる。
\[
\begin{aligned}
f_{Y(=X_1+X_2)}(y)=\int_0^{y}{f_{X_1}(x)f_{X_2}(y-x)\text{d}x}
\end{aligned}
\]
同じ指数分布の重ね合わせがガンマ分布になることを示す。
\[
\begin{aligned}
f_1(x;\mu) & =\frac{1}{\mu}e^{-\frac{x}{\mu}} \\
f_2(x;\mu) & =\int_0^x{f_1(y;\mu)f_1(x-y;\mu)\text{d}y} \\
& =\int_0^x{\frac{1}{\mu}e^{-\frac{y}{\mu}}\frac{1}{\mu}e^{-\frac{x-y}{\mu}}\text{d}y} \\
& =\frac{1}{\mu^2}\int_0^x{e^{-\frac{x}{\mu}}\text{d}y} \\
& =\frac{1}{\mu^2}xe^{-\frac{x}{\mu}} \\
f_3(x;\mu) & =\int_0^x{f_2(y;\mu)f_1(x-y;\mu)\text{d}y} \\
& =\int_0^x{\frac{1}{\mu^2}ye^{-\frac{y}{\mu}}\frac{1}{\mu}e^{-\frac{x-y}{\mu}}\text{d}y} \\
& =\frac{1}{\mu^3}\int_0^x{ye^{-\frac{x}{\mu}}\text{d}y} \\
& =\frac{1}{2\mu^3}x^2e^{-\frac{x}{\mu}} \\
f_n(x;\mu) & =\int_0^x{f_{n-1}(y;\mu)f_1(x-y;\mu)\text{d}y} \\
& =\frac{1}{(n-1)!\mu^n} x^{n-1} e^{-\frac{x}{\mu}} \\
\end{aligned}
\]
頑張れば、ガンマ分布の形を覚えていなくても、畳み込み計算から示すことが出来る。
指数分布の無記憶性を示す。
\[
\begin{aligned}
P(X>s+t|X>s) & =\frac{P(X>s+t)}{P(X>s)} \\
& =\frac{\int_{s+t}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}\text{d}x}{\int_{s}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}\text{d}x} \\
& =\frac{e^{-\frac{s+t}{\mu}}}{e^{-\frac{s}{\mu}}} \\
& =e^{-\frac{t}{\mu}} \\
& =P(X>t) \\
\end{aligned}
\]
指数分布とは，「コールセンターに次に電話がかかってくるまでにかかる時間」や「電化製品が次に壊れるまでの時間」などに用いられます。「昨日コールセンターに電話がかかってきたから，今日はかかってこないだろう」とか「昨日電化製品が壊れなかったから，今日は壊れないだろう」とか，そういうことはないわけですから，この事象には，無記憶性があるといえるわけですね。
そして、最後の (4) などは、図1が念頭にあると、より分かりやすいと思われる。
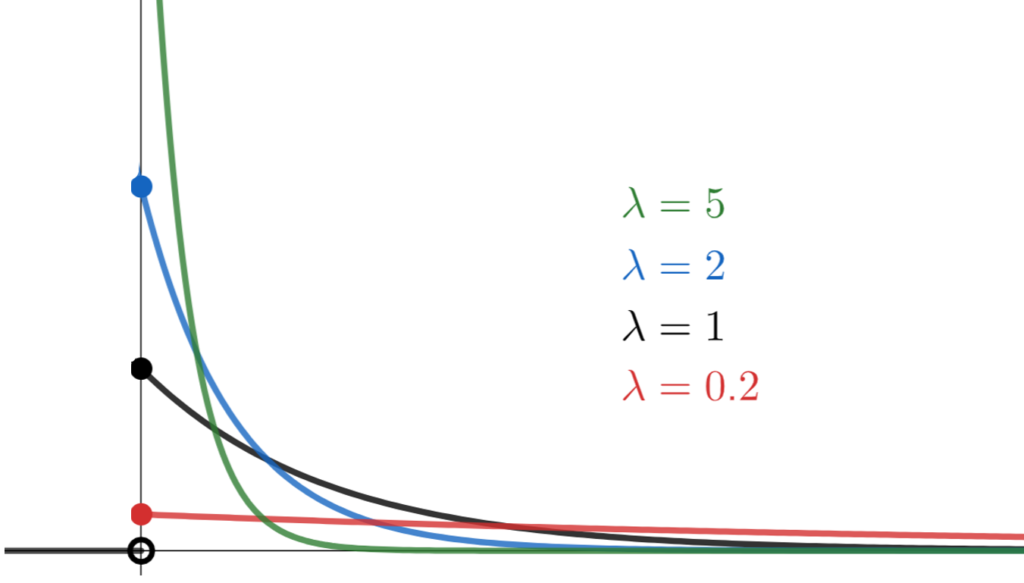
図1 パラメータ毎の指数分布
とある \(x\) でこのグラフを切った時に、最大の値を取るような \(\lambda\) は、ただ一つだけというのが、この問題の視覚的な理解であると思われる。