Skip to content

東京大学 情報理工学研究科 2023年度 数学 第3問

Author

hari64boli64

Description

丸石 \(○\) と四角い石 \(□\) をランダムに左から右に一直線上に一つずつ並べる。 \(0 < q < 1\) として、丸石を確率 \(1 - q\)、四角い石を確率 \(q\) で独立同一分布に従って並べていく。 \(M\) を正の整数として、四角い石が \(M\) 個連続して並べられた直後に並べることを停止する。 \(M = 4\) の場合の例を以下に示す。

  • 列 \(1\) \(○□□□□\)
  • 列 \(2\) \(□○□○○□□□□\)

停止後の石の数を表す確率変数を \(L\) とする。 上に示した列の場合、列 \(1\) と列 \(2\) はそれぞれ \(L = 5\)、\(L = 9\) となる。

並べている途中の状態を考える。\(k\) を非負整数とし、右端から四角い石が \(k\) 個連続している状態を \(C_k\) とする。例えば、\(M = 4\) の時に以下の列を考える。

  • 列 \(3\) \(○□□□○○□□\)
  • 列 \(4\) \(□○□○○\)

\(M = 4\) の場合を考えているため、列 \(3\) と列 \(4\) はまだ停止していない。 列 \(3\) は右端から四角い石が \(2\) 個連続しているので状態 \(C_2\) である。 列 \(4\) は右端に四角い石がないので状態 \(C_0\) である。 状態 \(C_k\) から \(n\) 個石を並べたときに初めて停止条件を満たす確率を \(a_{kn}\) とする。ここで \(n\) は非負整数である。 \(a_{kn}\) に対して以下のような母関数 \(A_k(t)\) を定義する。

\[ A_k(t) = \sum_{n=0}^{\infty} t^n a_{kn} \]

この時、以下の問いに答えよ。

(1) \(M = 1\) の時、\(L\) の平均と分散を求めよ。

(2) \(A_k(t)\) が満たす漸化式を求めよ。

(3) \(A_k(t)\) を \(q, M, t, k\) を用いて表せ。

(4) \(L\) の平均を求めよ。

Kai

(1)

\(M=1\) の場合、四角い石が出た時点で操作は停止される。

よって、状態 \(C_0\) から \(n\) 個石を並べたときに初めて停止条件を満たす確率 \(a_{0n}\) は、

\[ \begin{aligned} a_{0n} = \begin{cases} 0 & (n = 0 ) \\ (1-q)^{n-1}q & (n \geq 1) \end{cases} \end{aligned} \]

となる。

よって、

\[ \begin{aligned} \mathbb{E}[L] & = \sum_{n=0}^{\infty} na_{0n} \\ & = \sum_{n=1}^{\infty} n(1-q)^{n-1}q \\ & = q\frac{\text{d}}{\text{d}t}\left(\sum_{n=1}^{\infty}{t^n}\right)_{t=1-q} \\ & = q\frac{\text{d}}{\text{d}t}\left(\frac{1}{1-t}\right)_{t=1-q} \\ & = q\frac{1}{(1-(1-q))^2} \\ & = \frac{1}{q} \\ \end{aligned} \]
\[ \begin{aligned} \mathbb{V}[L] & = \mathbb{E}[L^2] - \mathbb{E}[L]^2 \\ & = \sum_{n=0}^{\infty} n^2a_{0n} - \frac{1}{q^2} \\ & = \sum_{n=1}^{\infty} n^2(1-q)^{n-1}q - \frac{1}{q^2} \\ & = \frac{2-q}{q^2}-\frac{1}{q^2} \\ & = \frac{1-q}{q^2} \\ \end{aligned} \]

となる。

(参考: これは幾何分布と呼ばれる分布である)

(2)

まず、状態 \(C_k(k>M)\) は定義されない事に注意する。(あるいは、定義されても \(A_k(t)=0\))

また、状態 \(C_k(k=M)\) の場合、既に操作は停止しているので、\(a_{k0}=1\) より、\(A_k(t)=1\) となる。

\(k<M\) の場合を考える。この時、状態遷移図は次のようになる。

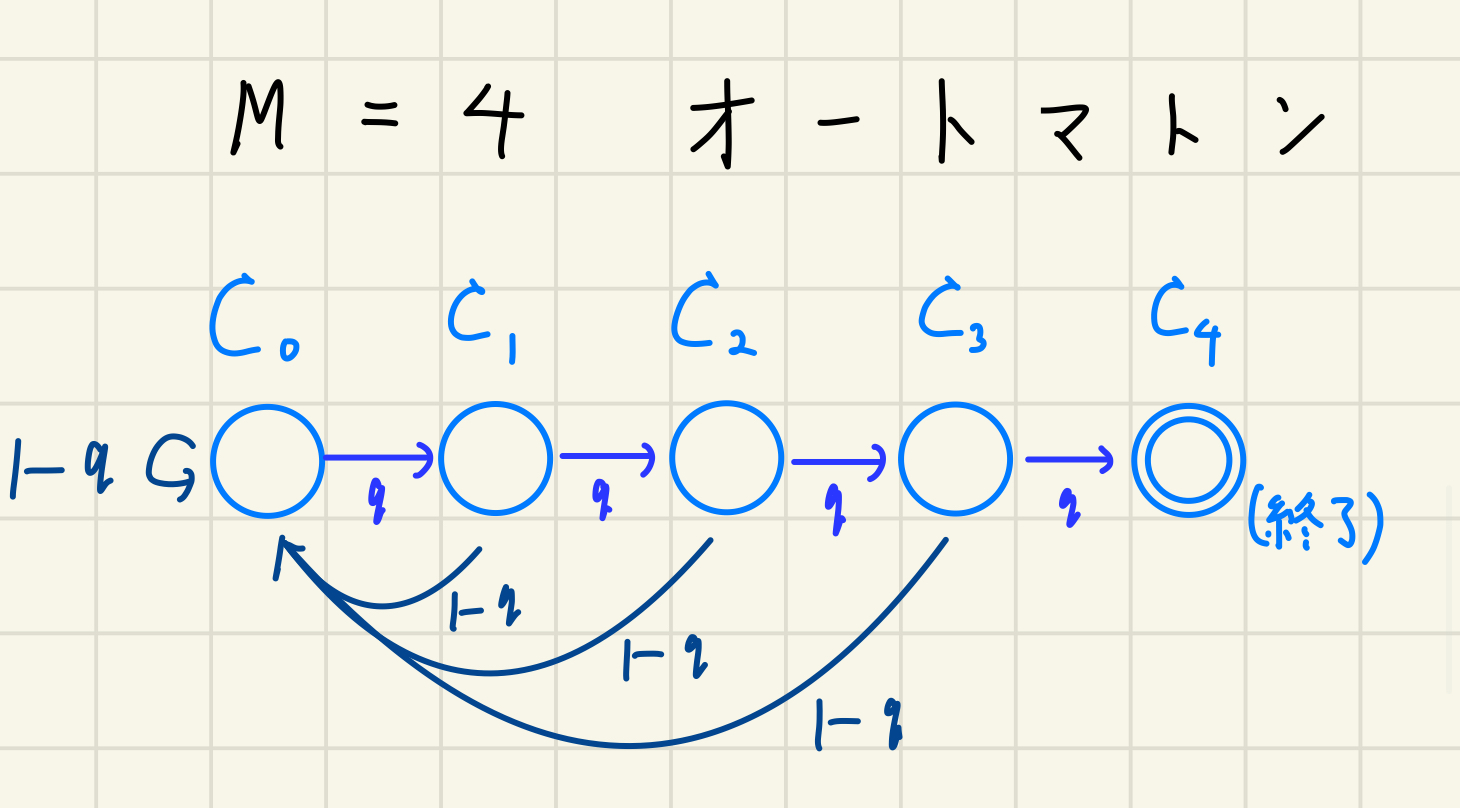
この図に示した通り、

  • 確率 \(q\) で四角い石が出る時、1個石を並べた上で、状態 \(C_{k+1}\) に遷移する。
  • 確率 \(1-q\) で丸石が出る時、1個石を並べた上で、状態 \(C_0\) に遷移する。

という関係性があるので、

\[ \begin{aligned} A_k(t)=qtA_{k+1}(t)+(1-q)tA_0(t) \quad (0 \leq k < M) \end{aligned} \]

となる。あるいは、同じことだが、

\[ \begin{aligned} A_{M-i}(t)=qtA_{M-i+1}(t)+(1-q)tA_0(t) \quad (0 < i \leq M) \end{aligned} \]

となる。

(なお、答えの書き方は色々あると思うが、恐らく上式のいずれかだけで十分だと思う。)

(3)

(2) の結果より、

\[ \begin{aligned} A_{M-1}(t) & =qtA_{M}(t)+(1-q)tA_0(t) \\ & =qt+(1-q)tA_0(t) \\ A_{M-2}(t) & =qtA_{M-1}(t)+(1-q)tA_0(t) \\ & =qt\left(qt+(1-q)tA_0(t)\right)+(1-q)tA_0(t) \\ & =q^2t^2+(1-q)qt^2A_0(t)+(1-q)tA_0(t) \\ & =q^2t^2+\left((1-q)qt^2+(1-q)t \right)A_0(t) \\ A_{M-3}(t) & =qtA_{M-2}(t)+(1-q)tA_0(t) \\ & =qt\left(q^2t^2+\left((1-q)qt^2+(1-q)t\right)A_0(t)\right)+(1-q)tA_0(t) \\ & =q^3t^3+\left((1-q)q^2t^3+(1-q)qt^2+(1-q)t\right)A_0(t) \\ \end{aligned} \]

となっていく。

つまり、

\[ \begin{aligned} A_{M-i}(t) & =q^it^i+\left(\sum_{j=0}^{i-1}(1-q)q^{j}t^{j+1}\right)A_0(t) \\ & =(qt)^i+(1-q)t\left(\sum_{j=0}^{i-1}(qt)^{j}\right)A_0(t) \\ & =(qt)^i+(1-q)t\left(\frac{1-(qt)^i}{1-qt}\right)A_0(t) \quad (0 < i \leq M) \end{aligned} \]

となる。

特に、\(i=M\) の場合を考えると、

\[ \begin{aligned} A_0(t) = (qt)^M+(1-q)t\left(\frac{1-(qt)^M}{1-qt}\right)A_0(t) \\ \end{aligned} \]

整理して、

\[ \begin{aligned} A_0(t) & =\frac{(qt)^M}{1-(1-q)t\left(\frac{1-(qt)^M}{1-qt}\right)} = \frac{(1-qt)(qt)^M}{1-t+t(1-q)(qt)^M} \\ A_{M-i}(t) & =(qt)^i+(1-q)t\left(\frac{1-(qt)^i}{1-qt}\right)\frac{(1-qt)(qt)^M}{1-t+t(1-q)(qt)^M} \quad (0 < i \leq M) \\ & = (qt)^i \frac{1-t+t(1-q)(qt)^{M-i}}{1-t+t(1-q)(qt)^M} \quad (0 < i \leq M) \\ A_{k}(t) & =(qt)^{M-k} \frac{1-t+t(1-q)(qt)^{k}}{1-t+t(1-q)(qt)^M} \quad (0 \leq k < M) \\ \end{aligned} \]

となる。

(4)

(3) の結果より、

\[ \begin{aligned} A_0(t) =\frac{(1-qt)(qt)^M}{1-t+t(1-q)(qt)^M} \end{aligned} \]

である。

(1) と同様の考え方から、答えは \(\left(\frac{\text{d}}{\text{d}t}A_0(t)\right)_{t=1}\) である。

よって、これを微分して、代入整理すると、

\[ \begin{aligned} \frac{1-q^M}{(1-q)q^M} \end{aligned} \]

となる。

(なお、\(M=1\)を代入すると、これは \(\frac{1}{q}\) となり、(1) の結果に一致する)

Additions

コードによって、正当性を検証する。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import random

import matplotlib.pyplot as plt


def trial(M: int, q: float):
    cnt = 0
    ans = 0
    while cnt < M:
        x = random.random()
        ans += 1
        if x < q:
            cnt += 1
        else:
            cnt = 0
    return ans


def main():
    for M in [1, 2, 3]:
        for q in [0.1, 0.2, 0.3, 0.4, 0.5]:
            answers = []
            for _ in range(10000):
                answers.append(trial(M, q))
            avg = sum(answers) / len(answers)
            # plt.title()
            # plt.hist(answers)
            # plt.show()
            print("=" * 10)
            print(f"{M=}, {q=}")
            print(f"{avg=}")
            print(f"{(1 - q**M) / ((1 - q) * (q**M))=}")


if __name__ == "__main__":
    main()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
M=1, q=0.1
avg=10.0076
(1 - q**M) / ((1 - q) * (q**M))=9.999999999999998
==========
M=1, q=0.2
avg=4.9994
(1 - q**M) / ((1 - q) * (q**M))=4.999999999999999
==========
M=1, q=0.3
avg=3.3353
(1 - q**M) / ((1 - q) * (q**M))=3.333333333333333
==========
M=1, q=0.4
avg=2.4801
(1 - q**M) / ((1 - q) * (q**M))=2.5
==========
M=1, q=0.5
avg=2.0025
(1 - q**M) / ((1 - q) * (q**M))=2.0
==========
M=2, q=0.1
avg=110.8138
(1 - q**M) / ((1 - q) * (q**M))=109.99999999999997
==========
M=2, q=0.2
avg=30.3796
(1 - q**M) / ((1 - q) * (q**M))=29.999999999999993
==========
M=2, q=0.3
avg=14.6192
(1 - q**M) / ((1 - q) * (q**M))=14.444444444444445
==========
M=2, q=0.4
avg=8.626
(1 - q**M) / ((1 - q) * (q**M))=8.749999999999998
==========
M=2, q=0.5
avg=5.9403
(1 - q**M) / ((1 - q) * (q**M))=6.0
==========
M=3, q=0.1
avg=1106.5573
(1 - q**M) / ((1 - q) * (q**M))=1109.9999999999998
==========
M=3, q=0.2
avg=153.216
(1 - q**M) / ((1 - q) * (q**M))=154.99999999999994
==========
M=3, q=0.3
avg=50.901
(1 - q**M) / ((1 - q) * (q**M))=51.48148148148149
==========
M=3, q=0.4
avg=24.4842
(1 - q**M) / ((1 - q) * (q**M))=24.374999999999993
==========
M=3, q=0.5
avg=13.7934
(1 - q**M) / ((1 - q) * (q**M))=14.0

確かに、大まかに一致しているため、正しいと考えられる。