東京大学 情報理工学研究科 2019年度 数学 第3問
Author
etsurin
Description
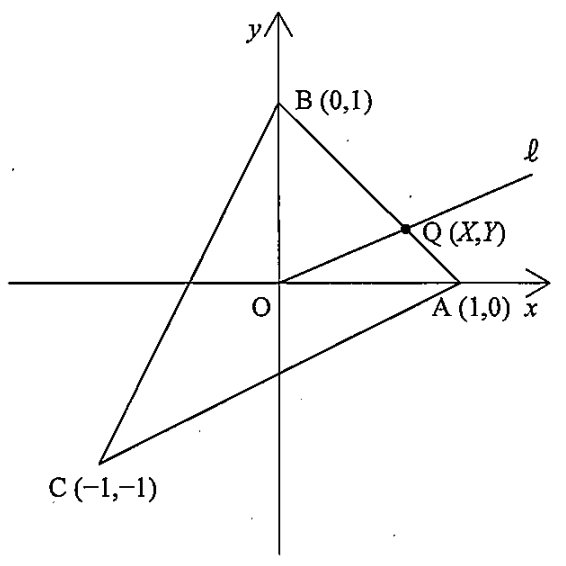
下図のように、平面上に三角形 \(ABC\) が与えられており、各頂点の座標は \(A\ (1,0)\)、\(B\ (0,1)\)、\(C\ (-1,-1)\) とする。
原点 \((0,0)\) を端点とする半直線 \(\ell\) をランダムに選ぶ。
すなわち、\(\Theta\) を区間 \([0, 2\pi)\) 上の一様分布に従う確率変数として
\[
\ell = \{ (r \cos \Theta, r \sin \Theta) \mid r \geq 0 \}
\]
とおく。この半直線 \(\ell\) と三角形 \(ABC\) の周との交点を \(Q\) とおく。
また、\(Q\) の座標を \((X, Y)\) とおく。ただし、\(X, Y\) は確率変数である。
以下の問いに答えよ。
(1) 点 \(Q\) が辺 \(AB\) 上にある確率を求めよ。
(2) 点 \(Q\) が辺 \(AB\) 上にあるという条件のもとでの \(X\) の期待値は \(1/2\) であることを示せ。
ただし、三角形 \(ABC\) が直線 \(y = x\) に関して対称であることを利用してよい。
(3) 点 \(Q\) が辺 \(BC\) 上にあるという条件のもとでの \(X\) の確率密度関数を、変数変換の公式
\[
f(x) = g(h(x)) \left| \frac{dh}{dx}(x) \right|
\]
を使って求めよ。
ただし、\(x\) は任意の実数とし、\(f\) と \(g\) はそれぞれ \(X\) と \(\Theta\) の確率密度関数を表し、\(h\) は \(\Theta = h(X)\) を満たす関数とする。
(4) 点 \(Q\) が辺 \(BC\) 上にあるという条件のもとでの \(X\) の期待値を \(\alpha\) とおく。
設問 (3) の結果を使って \(\alpha\) を求めよ。
(5) \(X\) の期待値 \(\mu\) を求めよ。
Kai
(1)
\(Q\) 在 \(AB\) 上,对应 \(\Theta \in [0, \frac{\pi}{2})\)
\[
P(Q \text{ is on } AB) = \frac{\frac{\pi}{2}}{2\pi} = \frac{1}{4}
\]
(2)
\(Q\) 在 \(AB\) 上的条件下,\(\Theta\) 的条件分布
\[
f_{AB}(\Theta) \sim U(0, \frac{\pi}{2})
\]
\[
f_{AB}(\Theta) = \frac{2}{\pi} \qquad 0 < \Theta < \frac{\pi}{2}
\]
\(AB\) 对应边 \(y = x+1\)。转化为极坐标 \(\rho \cos \Theta + \rho \sin \Theta = 1\)。
\[
x = \rho \cos \Theta = \frac{\cos \Theta}{\cos \Theta + \sin \Theta}
\]
\[
\begin{aligned}
E_{AB}(X) &= \frac{2}{\pi} \int_0^{\frac{\pi}{2}} \frac{\cos \Theta}{\cos \Theta + \sin \Theta} \text{d} \Theta \\
&= \frac{2}{\pi} \int_0^{\frac{\pi}{4}} \frac{\cos \Theta}{\cos \Theta + \sin \Theta} \text{d} \Theta - \frac{2}{\pi} \int_0^{\frac{\pi}{4}} \frac{\sin \theta}{\cos \theta + \sin \theta} \text{d} \theta \\
&(\text{拆分区间,后项作变量代换 } \theta = \frac{\pi}{2} - \Theta) \\
&= \frac{2}{\pi} \int_0^{\frac{\pi}{4}} \frac{\cos \Theta + \sin \Theta}{\cos \Theta + \sin \Theta} \text{d} \Theta \\
&= \frac{1}{2}
\end{aligned}
\]
(3)
\(Q\) 在 \(BC\) 上的条件下,\(\Theta\) 的条件分布
\[
f_{BC}(\Theta) \sim U(\frac{\pi}{2}, \frac{5\pi}{4})
\]
\[
f_{BC}(\Theta) = \frac{4}{3\pi} \qquad \frac{\pi}{2} \leq \Theta < \frac{5\pi}{4}
\]
\(BC\) 对应边 \(y=2x+1\)。转化为极坐标 \(\rho \sin \Theta = 2 \rho \cos \Theta + 1\)。
\[
x = \rho \cos \Theta = \frac{\cos \Theta}{\sin \Theta - 2 \cos \Theta} = \frac{1}{\tan \Theta - 2}
\]
\[
f_{BC}(\Theta) \text{d}\Theta = f_{BC}(x) \text{d}x
\]
\[
f_{BC}(x) = f_{BC}(h(x))h'(x) \qquad \Theta = h(x)
\]
\[
\tan \Theta = 2 + \frac{1}{x} \qquad \Theta = \arctan (2 + \frac{1}{x}) = h(x)
\]
\[
|h'(x)| = \left \lvert - \frac{1}{x^2} \frac{1}{1+(2+\frac{1}{x})^2} \right \rvert = \frac{1}{5x^2 + 4x + 1}
\]
\[
f_{BC}(x) = \frac{4}{3 \pi} \frac{1}{5x^2+4x+1} \qquad x \in (-1, 0]
\]
(4)
\[
\begin{aligned}
\alpha &= \int_{-1}^0 \frac{4}{3 \pi} \frac{x}{5x^2+4x+1} \text{d} x \\
&= \frac{4}{3 \pi} \int_{-1}^0 \frac{x}{5(x+\frac{2}{5})^2 + \frac{1}{5}} \text{d}x \\
&= \frac{4}{3 \pi} \int_{-\frac{3}{5}}^{\frac{2}{5}} \frac{x - \frac{2}{5}}{5x^2 + \frac{1}{5}} \text{d}x \\
&= \frac{4}{3 \pi} \int_{-\frac{3}{5}}^{\frac{2}{5}} \frac{x}{5x^2 + \frac{1}{5}} \text{d}x - \frac{8}{15 \pi} \int_{-\frac{3}{5}}^{\frac{2}{5}} \frac{1}{5x^2 + \frac{1}{5}} \text{d}x \\
&= \frac{10}{3 \pi} \int_{-\frac{3}{5}}^{-\frac{2}{5}} \frac{1}{25 x^2 + 1} \text{d}(x^2) - \frac{8}{3\pi} \int_{-\frac{3}{5}}^{\frac{2}{5}} \frac{1}{25x^2 + 1} \text{d}x \\
&= \frac{2}{15 \pi} \ln (25x^2 + 1) \bigg|_{\frac{9}{25}}^{\frac{4}{25}} - \frac{8}{15 \pi} \arctan (5x) \bigg|_{-\frac{3}{5}}^{\frac{2}{5}} \\
&= -\frac{2}{15 \pi} \ln 2 - \frac{8}{15 \pi} (\arctan(2) - \arctan(-3))
\end{aligned}
\]
\(\tan (\theta_1) = 2, \tan (\theta_2) = -3\), 则 \(\tan(\theta_1 - \theta_2) = \frac{\tan \theta_1 - \tan \theta_2}{1 - \tan \theta_1 \tan \theta_2} = -1\)。\(\theta_1 - \theta_2 = \frac{3 \pi}{4}\)。
\[
\alpha = -\frac{2}{5} - \frac{2}{15 \pi} \ln 2
\]
(5)
\(AC\) 对应边 \(y = \frac{1}{2}(x - 1)\), 设 \(AC\) 边上 \(x\) 的期待值为 \(\beta\)。注意到 \(AC, BC\) 关于直线 \(y = x\) 对称。即 \((\alpha,2\alpha + 1) , (\beta,\frac{1}{2}(\beta - 1))\) 关于直线 \(y = x\) 对称。
\[
\left\{
\begin{aligned}
&\frac{\alpha + \beta}{2} = \frac{2\alpha + 1 + \frac{1}{2}(\beta - 1)}{2} \\
&\frac{\frac{1}{2}(\beta - 1) - (2\alpha + 1)}{\beta - \alpha} = -1 \\
\end{aligned}
\right.
\]
\[
\beta = 2\alpha + 1 = \frac{1}{5} - \frac{4}{15\pi} \ln 2
\]
令 \(x = g(\Theta)\) , 这里 \(g(\Theta)\) 是分段函数, 对应边 \(AB , BC , AC\) 三条边上时的情况。
\[
\begin{aligned}
E(X) &= \int_0^{2\pi}f(\Theta)g(\Theta)\text{d}\Theta \\
&= \frac{1}{2\pi} \int_0^{\frac{\pi}{2}}g(\Theta)\text{d}\Theta + \frac{1}{2\pi}\int_{\frac{\pi}{2}}^{\frac{5\pi}{4}}g(\Theta)\text{d}\Theta + \frac{1}{2\pi}\int_{\frac{5\pi}{4}}^{2\pi}g(\Theta)\text{d}\Theta \\
&= \frac{1}{4}E_{AB}(X) + \frac{3}{8}E_{BC}(X) + \frac{3}{8}E_{AC}(X) \\
&= \frac{1}{4} \times \frac{1}{2} + \frac{3}{8}(-\frac{2}{5} - \frac{2}{15\pi}\ln2) + \frac{3}{8}(\frac{1}{5} - \frac{4}{15\pi}\ln2) \\
&= \frac{1}{20} - \frac{3}{20\pi}\ln2
\end{aligned}
\]
