東京大学 情報理工学系研究科 電子情報学専攻 2024年度 専門 第5問

Author

Josuke

Description

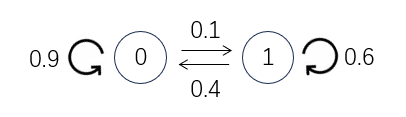
The source \(S\) is a first-order Markov information source outputting \(0\) and \(1\). \(0\) is followed by \(0\) with a probability of \(0.9\) and \(1\) is followed by \(1\) with a probability of \(0.6\). The following may be used. \(\log_23 = 1.58 , \log_25 = 2.32\). For the calculations, two significant digits are sufficient.

(1) Show a state transition diagram of the source \(S\).

(2) Obtain the probability of each \(0\) and \(1\) output from the source \(S\).

(3) Obtain the entropy of the source \(S\).

Assume the following four methods of coding to compress the output symbols of the source \(S\).

a. fixed-length coding of fixed-length symbol sequences

b. variable-length coding of fixed-length symbol sequences

c. fixed-length coding of variable-length symbol sequences

d. variable-length coding of variable-length symbol sequences

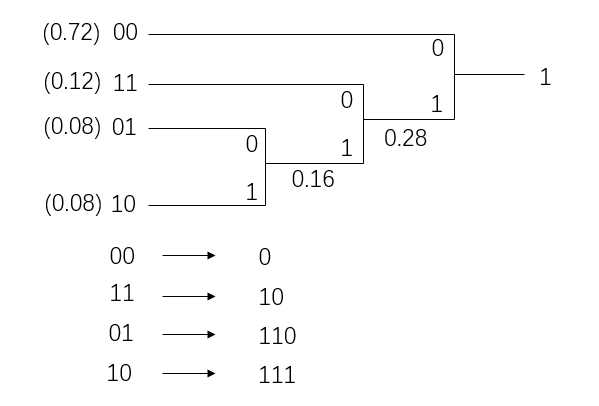
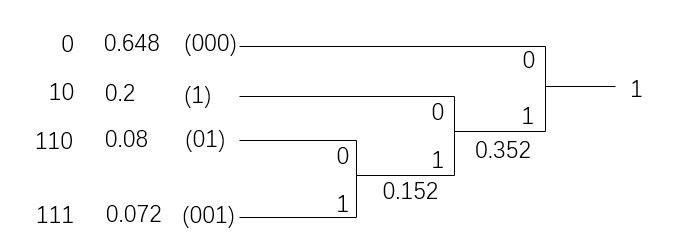
Consider the fixed-length symbol sequences as \(00 , 01 , 10\) and \(11\) , and the variable-length symbol sequences as \(000 , 001 , 01 ,\) and \(1\) that are \(0\)'s run lengths up to length \(3\). The variable-length coding is Huffman coding consisting of \(0\) and \(1\).

(4) Obatain the probability of each of the fixed-length symbol sequences of \(00 , 01 , 10 ,\) and \(11\).

(5) In the case b , show the Huffman code and obtain the average code length per symbol of the sources \(S\) .

(6) Obtain the probability of each of the variable-length symbol sequences of \(000 , 001 ,01 ,\) and \(1\).

(7) In the case c , obtain the average code length per symbol of the source \(S\) .

(8) Show the Huffman code for the case d and obtain the average code length per symbol of the source \(S\).

(9) Arrange the methods of a , b , c , and d from the shortest to the longest in terms of the average code length.

Kai

(1)

(2)

\[ \left\{ \begin{aligned} &0.9w_0 + 0.4w_1 = w_0 \\ &0.1w_0 + 0.6w_1 = w_1 \\ &2_0 + w_1 = 1 \end{aligned} \right. \]

\[ w_0 = 0.8 , w_1 = 0.2 \]

\[ \left\{ \begin{aligned} P(0) = 0.8 \times 0.9 + 0.2 \times 0.4 \\ P(1) = 0.8 \times 0.1 + 0.2 \times 0.6 \\ \end{aligned} \right. \]

\[ P(0) = 0.8 , P(1) = 0.2 \]

(3)

\[ \begin{aligned} H(s) &= - (0.8\log0.8 + 0.2\log0.2) \\ &= \frac{4}{5}\log\frac{5}{4} + \frac{1}{5}\log5 \\ &= \log5 - 1.6 \\ &= 0.72 \end{aligned} \]

(4)

\[ \begin{aligned} P(00) &= 0.8 \times 0.9 = 0.72 \\ P(01) &= 0.8 \times 0.1 = 0.08 \\ P(10) &= 0.2 \times 0.4 = 0.08 \\ P(11) &= 0.2 \times 0.6 = 0.12 \\ \end{aligned} \]

(5)

\[ \begin{aligned} \overline{L} &= (0.72 \times 1 + 0.12 \times 2 + 0.16 \times 3) / 2 \\ &= (0.72 + 0.24 + 0.48) / 2 \\ &= 0.72 \end{aligned} \]

(6)

\[ \begin{aligned} P(000) &= 0.8 \times 0.9 \times 0.9 = 0.648 \\ P(001) &= 0.8 \times 0.9 \times 0.1 = 0.072 \\ P(01) &= 0.8 \times 0.1 = 0.08 \\ P(1) &= 0.2 \\ \end{aligned} \]

(7)

\[ \begin{aligned} \overline{L} &= \frac{2}{0.72 \times 3 + 0.08 \times 2 + 0.2 \times 1} \\ &= \frac{2}{2.52} \approx 0.794 \end{aligned} \]

(8)

\[ \begin{aligned} \overline{L} &= \frac{0.648 \times 1 + 0.2 \times 2 + 1.52 \times 3}{2.52} \\ &= 0.597 \end{aligned} \]

(9)

d,b,c,a