東京大学 情報理工学系研究科 電子情報学専攻 2023年度 専門 第5問

Author

Josuke

Description

Answer the following questions about discrete signal processing.

(1) Show the definition of the \(\mathcal{Z}\)-transform \(X(z)\) of a discrete signal sequence \(x_n(n=0,1,2,\dots)\) defined for \(n \ge 0\) where \(z\) is a complex number.

(2) By using the definition, find the \(\mathcal{Z}\)-transform of a geometric sequence \(x_n = p^n\) where \(p\) is a real number.

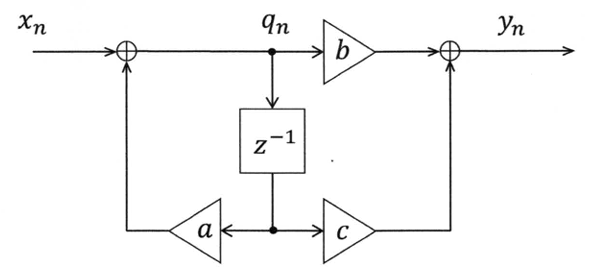
(3) We consider the zero state response of the discrete time system shown in the figure below ,where \(a,b\) and \(c\) are real numbers. Give \(X(z)\) and \(Y(z)\) by using the \(\mathcal{Z}\)-tranform \(Q(z)\) of the system's internal state \(q_n\). Here, \(X(z)\) and \(Y(z)\) are the \(\mathcal{Z}\)-tranforms of the system's input \(x_n\) and output \(y_n\), respectively.

(4) Give the transfer function \(H(z)\) of the system.

(5) Next, we find the system's frequency response by using the transfer function \(H(z)\). Consider the input sequnence \(x_n = e^{jn\omega T}\) sampled at the interval \(T\) from a complex exponential function \(x(t) = e^{j\omega t}(t \ge 0)\). Derive \(Y(z)\) and then find the output sequence \(y_n\).

Kai

(1)

\[ X(z) = \sum_{n=0}^{+\infty}x(n)z^{-n} \]

(2)

\[ X(z) = \sum_{n=0}^{+\infty}p^nz^{-n} = \sum_{n=0}^{+\infty}(pz^{-1})^n = \frac{1}{1 - pz^{-1}} \]

(3)

\[ \begin{aligned} X(z) &+ az^{-1}Q(z) = Q(z) \\ X(z) &= (1 - az^{-1})Q(z) \\ Y(z) &= bQ(z) + cz^{-1}Q(z) \\ &= (b + cz^{-1})Q(z) \end{aligned} \]

(4)

\[ H(z) = \frac{Y(z)}{X(z)} = \frac{b + cz^{-1}}{1 - az^{-1}} = \frac{b}{1 - az^{-1}} + \frac{cz^{-1}}{1 - az^{-1}} \]

(5)

\[ \begin{aligned} X(z) &= \frac{1}{1 - e^{j\omega T}z^{-1}} \qquad h[n] = ba^n + ca^{n-1} \\ Y(z) &= \frac{b + cz^{-1}}{(1 - az^{-1})(1 - e^{j\omega T}z^{-1})} \\ y[n] &= \sum_{k=0}^{+\infty}e^{j\omega kT}(ba^{n-k} + ca^{n-k-1}) \\ &= ba^{n} \sum_{k=0}^{+\infty}(e^{j\omega T}a^{-1})^k + ca^{n-1} \sum_{k=0}^{+\infty}(e^{j\omega T}a^{-1})^k \\ &= \frac{ba^n}{1 - a^{-1}e^{j\omega T}} + \frac{ca^{n-1}}{1 - a^{-1}e^{j\omega T}} \\ &=\frac{(ba + c)a^{n-1}}{1 - a^{-1}e^{j\omega T}} \end{aligned} \]