東京大学情報理工学系研究科電子情報学専攻 2020年度専門第5問

Author

Description

離散時間信号 \(x\) の出力が，図のような確率密度関数 \(p(x)\) に従うとする. 以下の問いに答えよ．\(\log_23 = 1.58, \log_25 = 2.32\) とする．

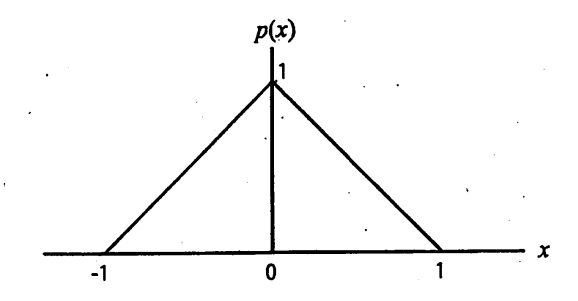
(1) 量子化器 \(Q_0\) は，信号 \(x\) の出力のレンジ \([-1,1]\) を均等に \(5\) 分割して; \(5\) レベルの量子化を行う．その量子化出力を入力信号値の小さい方から \(q_1,q_2,q_3,q_4,q_5\) とする．それぞれの出現確率を求めよ．

(2) \(Q_0\) の量子化出力のエントロピーを求めよ．

(3) \(Q_0\) の量子化出力を最も効率よく表現する \(2\) 元符号 \(C_0\) を \(1\) つ求めよ．

(4) \(C_0\) の平均符号長を求めよ．

(5) 出力のエントロピーを最大とする \(5\) レベル量子化器 \(Q_1\) の量子化の境界 \(d_i(i = 1,2,3,4)\) を求めよ．量子化の境界を \(d_{i-1},d_i\) とした時，量子化操作 \(Q()\) は下式で与えられる．

\[ Q(d_{i-1} \le x < d_i) = q_i \]

ただし，\(d_0 = -1 ,d_5 = 1\) である．

(6) 信号の再生には,各量子化出力 \(q_i\) に対して，対応する量子化区間内の一つの値を量子化代表値として割り当てる．信号値と再生値の平均 \(2\) 乗誤差により，量子化誤差を定義する．量子化器出力 \(q_i\) に対して，量子化誤差を最小化する量子化代表値 \(\widetilde{x}_i\) は下式で与えられることを示せ．

\[ \widetilde{x}_i = \frac{\int_{d_{i-1}}^{d_i}xp(x)dx}{\int_{d_{i-1}}^{d_i}p(x)dx} \]

(7) 量子化器 \(Q_1\) の \(\widetilde{x}_i(i=1,2,3,4,5)\) を求めよ．

Kai

(1)

範囲 \([−1, 1]\) を均等に \(5\) 分割しているので、\(q_1, q_2, q_3, q_4, q_5\) の領域はそれぞれ \([−1, −0.6]、[−0.6, −0.2]、[−0.2, 0.2]、[0.2, 0.6]、[0.6, 1]\) である。

よって、それぞれの領域の図形の面積を計算して

\[ \begin{aligned} q_1 &= q_5 = \frac{1}{2} \cdot 0.4^2 = \frac{2}{25} \\ q_2 &= q_4 = \frac{1}{2} \cdot 0.8^2 - q_1 = \frac{6}{25} \\ q_3 &= 1 - (q_1 + q_2 + q_4 + q_5) = \frac{9}{25} \end{aligned} \]

(2)

エントロピーは \(-\sum_{A \in \Omega}P(A)\log P(A)\) と表せ、問題部により \(\log3 = 1.58, \log5 = 2.32\) だから求めるエントロピーは

\[ \begin{aligned} &-(2\frac{2}{25}\log\frac{2}{25} + 2\frac{6}{25}\log\frac{6}{25} + \frac{9}{25}\log\frac{9}{25}) \\ &= (\frac{4}{25}(\log2 - 2\log5)) + \frac{12}{25}(\log2 + \log3 - 2\log5) + \frac{9}{25}(2\log3 - 2\log5) \\ &= (\frac{16}{25}\log2 + \frac{30}{25}\log3 - 2\log5) \\ &= -(0.64 + 1.896 - 4.64) = 2,104 \end{aligned} \]

(3)

ハフマン符号によって符号化する。\(q_1\) から \(q_5\) までをノードとして、最も確率の低いノードを合併し、それらのノードの確率の和を確率とするノードを作る。これをノードが最後の \(1\) つになるまで続ける。そして、最後に残ったノードからたどって、左端のノードに戻る際に通ったエッジから符号を決める。上部のエッジを \(1\) 、下部のエッジを \(0\) とする。これを図にすると以下のようになる。

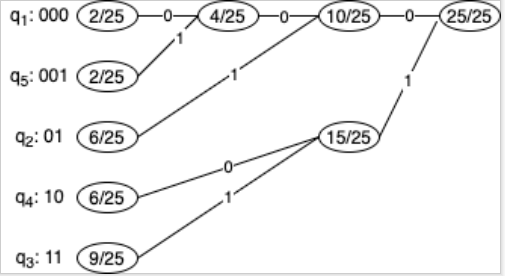
よって、\(2\) 元符号 \(C_0\) は以下のように表せる。

\(q_1\)	000
\(q_2\)	01
\(q_3\)	10
\(q_4\)	11
\(q_5\)	001

(4)

(3) で求めた符号から求める符号長は

\[ 2 \cdot 3\frac{2}{25} + 2 \cdot 2\frac{6}{25} + 2\frac{9}{25} = 2.16 \]

(5)

エントロピーが最大となるとき、それぞれの信号値は等確率 \(\frac{1}{5}\) となる。

よって、それぞれの信号値が \(\frac{1}{5}\) となるように \(d_i\) を求める。

\(d_1 - d_0 = x_1(>0)\) として、\(\frac{1}{2}x_1^2 = \frac{1}{5}\) となる。これを解いて \(x_1 = \sqrt{\frac{2}{5}}\) となる。よって、\(d_1 = -1 + \sqrt{\frac{2}{5}}\) となり、対称性から \(d_2 = 1 - \sqrt{\frac{2}{5}}\)

同様に考えて、\(d_2 = -1 + \frac{2}{\sqrt{5}},d_3 = 1 - \frac{2}{\sqrt{5}}\)

(6)

量子化誤差は信号値と再生値の平均二乗誤差だから

\[ \int_{d_{i-1}}^{d_1}(x - x_i)^2p(x)dx \]

と書ける。これを \(x_i\) に関して微分すると

\[ -2\int_{d_{i-1}}^{d_i}xp(x)dx + 2x_i\int_{d_{i-1}}^{d_i}p(x)dx \]

となる。量子化誤差が最小のとき、これは \(0\) となるからこのときの \(x_i = \widetilde{x}_1\) は以下のように表せる。