東京大学 情報理工学系研究科 電子情報学専攻 2020年度 専門 第1問
Author
diohabara
Description
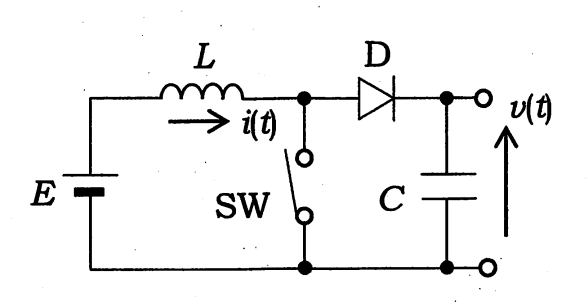
図に示す,定電圧電源 (電圧 \(E\)), スイッチ (記号 \(SW\)) , ダイオード (記号 \(D\)), コイル (インダクタンス \(L\)), コンデンサ (キャパシタンス \(C\)), 端子で構成される昇圧回路を考える.時刻を \(t\) とし,コイルを流れる電流を \(i(t)\) , 端子の両端の電圧を \(v(t)\) とする (それぞれの方向は図を参照のこと).また,ダイオードの順方向電圧は無視でき,時刻 \(t=0\) で \(i(0)=0,v(0)=E\) とする.このとき,以下の問いに答えよ.
(1) \(t=0\) から \(T_0\) の時間,スイッチを短絡させる. \(0 \le t < T_0\) について, \(i(t)\) を求めよ.
(2) \(t=T_0\) に,スイッチを開放する.スイッチを開放してから \(i(t)\) が \(0\) に戻るまでの時間を \(T_1\) とする.\(T_0 \le t < T_0\) における \(i(t)\) を求め, \(T_1\) も求めよ.
\(t=0\) から,上述の操作 (\(T_0\) 時間短絡し,\(T_1\) 時間開放させる) を \(n\) 回繰り返す.\(T_0\) および \(T_1\) は定数,\(n\) は \(1\) 以上の整数とする.
(3) \(i(T_0 + T_1) = 0\)ならば, \(i(n(T_0 + T_1)) = 0\) であることを定性的に説明せよ.
(4) \(v(n(T_0 + T_1))\) を求めよ.
Kai
(1)
スイッチを短絡させると、以下の回路方程式が成り立つ。
\[
L\frac{di(\tau)}{d\tau} = v(t)
\]
電源は定電圧電源なので \(v(t) = v(0) = E\) であり、\(\tau = [0,t]\) 上で \(\tau\) に関して積分して整理すると
\[
i(t) - i(0) = \frac{E}{L}t
\]
問題文より \(t = 0\) で \(i(0) = 0\) だから
\[
i(t) = \frac{E}{L}t
\]
(2)
スイッチを開放すると、\(t = [T_0, T_0 + T_1)\) において以下の回路方程式が成り立つ。
\[
L\frac{di(t)}{dt} + \frac{1}{C}\int_{T_0}^t i(\tau)d\tau = E
\]
両辺を微分して整理すると
\[
\begin{aligned}
0 &= L\frac{d^2i(t)}{dt^2} + \frac{1}{C}i(t) \\
\frac{d^2i(t)}{dt^2} &= - \frac{1}{LC}i(t)
\end{aligned}
\]
よって、\(i(t)\) の一般解は
\[
i(t) = A\sin\frac{1}{\sqrt{LC}}t + B\cos\frac{1}{\sqrt{LC}}t
\]
と書ける.
(1) より \(i(T_0) = \frac{E}{L}T_0\) であり \(\frac{di(t)}{dt}\bigg|_{t = T_0} = 0\)
\(\frac{di(t)}{dt} = \frac{A}{\sqrt{LC}}\cos\frac{t}{\sqrt{LC}} - \frac{B}{\sqrt{LC}}\sin\frac{t}{\sqrt{LC}}\) より
\[
\frac{di(t)}{dt}\bigg|_{t = T_0} = \frac{A}{\sqrt{LC}}\cos\frac{T_0}{\sqrt{LC}} - \frac{B}{\sqrt{LC}}\sin\frac{T_0}{\sqrt{LC}} = 0
\]
よって
\[
A = B\tan\frac{T_0}{\sqrt{LC}}
\]
また
\[
\begin{aligned}
i(T_0) &= \frac{A}{\sqrt{LC}}\cos\frac{T_0}{\sqrt{LC}} - \frac{B}{\sqrt{LC}}\sin\frac{T_0}{\sqrt{LC}} \\
&= B\bigg(\sin\frac{T_0}{\sqrt{LC}}\tan\frac{T_0}{\sqrt{LC}} + \cos\frac{T_0}{\sqrt{LC}}\bigg) \\
&= B\frac{\sin^2\frac{T_0}{\sqrt{LC}} + \cos^2\frac{T_0}{\sqrt{LC}}}{\cos\frac{T_0}{\sqrt{LC}}} \\
&= \frac{B}{\cos\frac{T_0}{\sqrt{LC}}}
\end{aligned}
\]
よって、\(i(T_0) = \frac{E}{L}T_0\) より
\[
\begin{aligned}
B &= \frac{E}{L}T_0\cos\frac{T_0}{\sqrt{LC}} \\
A &= B\tan\frac{T_0}{\sqrt{LC}} = \frac{E}{L}T_0\sin\frac{T_0}{\sqrt{LC}}
\end{aligned}
\]
よって
\[
\begin{aligned}
i(t) &= \frac{E}{L}T_0\sin\frac{T_0}{\sqrt{LC}}\sin\frac{t}{LC} + \frac{E}{L}T_0\cos\frac{T_0}{\sqrt{LC}}\cos\frac{t}{LC} \\
&= \frac{E}{L}T_0\cos\frac{1}{\sqrt{LC}}(t - T_0)
\end{aligned}
\]
これが \(t \le T_0\) で最初に \(0\) となるのは、\(\frac{1}{\sqrt{LC}}(t - T_0) = \frac{\pi}{2}\) のときなので
\[
\frac{1}{\sqrt{LC}}((T_0 + T_1) - T_0) = \frac{\pi}{2}
\]
\[
\therefore T_1 = \frac{\pi\sqrt{LC}}{2}
\]
(3)
ダイオードがあるため、コンデンサにかかる電圧 \(v(t)\) は常に単調増加する。したがって、スイッチを開放しているときにコイルに流れる電流の時間変化
\[
\frac{di(t)}{dt} = \frac{E - v(t)}{L}
\]
は単調減少する。これはつまり、回数を重ねるごとにスイッチ解放後に電流が減少するスピードが早くなるということ。だから、\(i = 0\) となるまでにかかる時間は \(T_1\) からどんどん短くなっていく。
よって、各操作でスイッチを開放した後 \(T_1\) 時間後までに必ず \(i = 0\) となっているはずな
ので、\(i(n(T_1 + T_0)) = 0\) と言える。
(4)
簡単のため、\(v_k = v(k(T_0 + T_1))\) とおく。
\(k(T_0 + T_1) \le k(T_0 + T_1) + T_0\) のとき、回路に流れる電流は (1) と同様にして
\[
\begin{align}
E &= L\frac{di(t)}{dt} ,i(k(T_0 + T_1)) = 0 \\
\therefore i(t) &= \frac{E}{L}(t - k(T_0 + T_1)) \tag{1}
\end{align}
\]
よって、\(t = k(T_0 + T_1) + T_0\) のとき \(i(t) = \frac{E}{L}T_0\) である。
\(k(T_0 + T_1) + T_0 \le t < (k + 1)(T_0 + T_1)\) の間について、電源がした仕事とコイル・コンデンサのエネルギーの変化分は等しいので
\[
E \cdot C (v_{k+1} - v_k) = \big(\frac{1}{2}L \cdot 0^2 + \frac{1}{2}Cv_{k+1}^2\big) + \big(\frac{1}{2}L(\frac{E}{L}T_0)^2 + \frac{1}{2}Cv_k^2\big)
\]
\[
(v_{k+1} + E)^2 = (v_k - E)^2 + \frac{E^2}{LC}T_0^2
\]
\(v_0 = v(0) = E\) に注意してこれを解くと
\[
(v_n - E)^2 = n \cdot \frac{E^2}{LC}T_0^2
\]
\[
\therefore v_n = E\big(1 + T_0\sqrt{\frac{n}{LC}}\big)
\]
