東京大学 情報理工学系研究科 電子情報学専攻 2018年度 専門 第2問
Author
Description
以下のような剰余計算回路 \(C\) を設計する。\(C\) はクロックに同期して毎サイクル \(2\) ビットの整数 \(I_1I_0\) を受け取り続ける。\(C\) には \(2\) ビット出力 \(O_1O_0\) が備わっており、それまでに入力された値の総計を \(4\) で割った剰余を出力し続ける。入力、出力とも符号無し整数として表現され、 \(I_1\) および \(O_1\) を \(MSB\) とする。回路の初期状態では、入力値の総計は \(0\) であるとする。以下の問いに答えよ。
(1) \(C\) について、出力がその回路状態からのみ決まる回路とし設計するとき、状態遷移図を示せ。最も状態数が少ない設計とすること。
(2) (1) で設計した状態遷移図の状態遷移表を下表のように示せ。ここで状態は \(n\) ビットのレジスタで保持することを想定し、\(S_{n-1}\dots S_0\) のように表している。また、\(S_{n-1}'\dots S_0'\) は次状態を表している。状態レジスタから出力を生成する回路が最も簡単になるように状態を割り振ること。
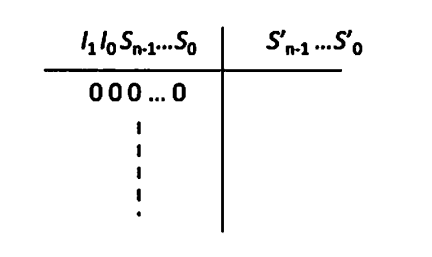
(3) 状態レジスタの各ビットの次状態を決定する論理式を、それぞれ加法標準形(積項を+でつないで出来た式)で示せ。カルノー図を用いて項数を最小とすること。
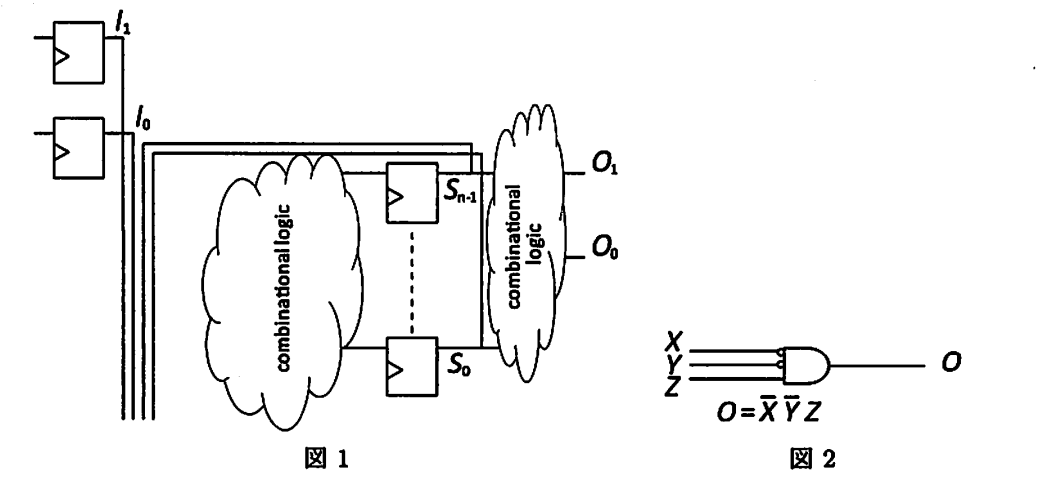
(4) 図 \(1\) を具体化する形で、(3) で導いた論理式を実現する回路をANDゲート、ORゲート、NOTゲート、およびDフリップ・フロップの組み合わせにて示せ。図 \(2\) のように、入力値の反転を意味する記法を用いても良い。また、クロックの分配線は省略して良い。フリップ・フロップは理想的であると仮定する。
Kai
(1)
求める最も状態数の少ない状態遷移図は次の通り。
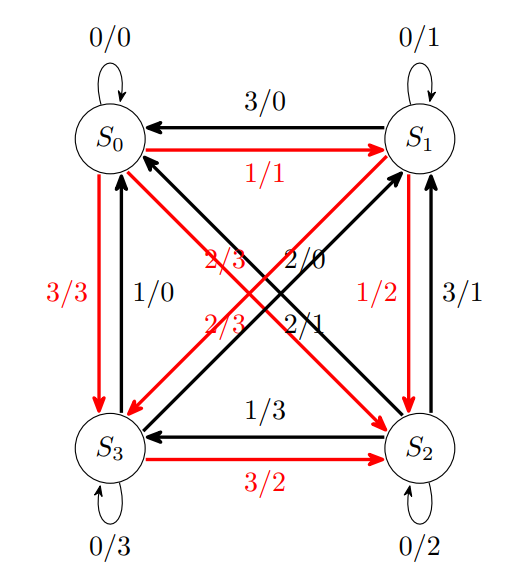
(2)
| \(I_1\) | \(I_0\) | \(S_1\) | \(S_0\) | \(S_1'\) | \(S_0'\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
(3)
カルノー図は次の通り。
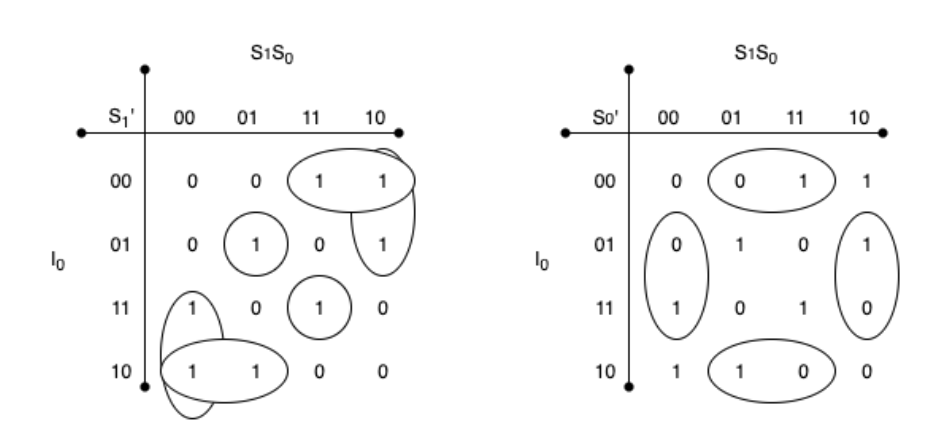
よって加法標準形は
(4)
TODO