東京大学 情報理工学系研究科 電子情報学専攻 2015年度 専門 第5問

Author

diohabara

Description

以下のような状態遷移図で示される二元単純マルコフ情報源を考える。

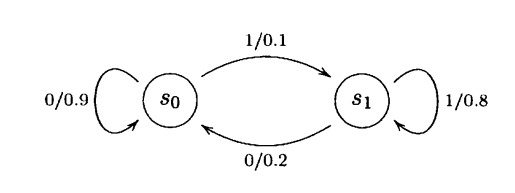
以下の問いに答えよ。

(1) 状態 \(s_0,s_1\) の定常確率 \(w_0,w_1\) を求めよ。

(2) 定常状態において出力 \(1\) の発生する確率を求めよ。

(3) 出力系列から, 直前および直後が \(0\) である \(1\) の連続 (\(1\) のラン)を任意に一つ取り出した時, その長さが \(1,2,k\) である確率をそれぞれ求めよ。

(4) \(1\) のランの平均長を求めよ。

(5) この情報源のエントロピーを求めよ。

(6) (2) で求めた生成確率でランダムに \(1\) が発生する情報源のエントロピーを求めよ。この値と (5) で求めた値の違いについて論ぜよ。

(なお、計算に当たっては, \(\log_23 = 1.58 ,\log_25 = 2.32\) を必要に応じて用いよ。)

Kai

(1)

状態遷移図より以下の方程式が成り立つ

\[ \begin{aligned} w_0 &= 0.9w_0 + 0.2w_1 \\ w_1 &= 0.1w_0 + 0.8w_1 \\ w_0 &+ w_1 = 1 \end{aligned} \]

これを解いて、

\[ (w_0,w_1) = (\frac{2}{3},\frac{1}{3}) \]

(2)

(1) より求める確率は

\[ 0.1w_0 + 0.8w_1 = \frac{1}{3} \]

(3)

長さ \(k\) のランの場合、最初の \(01\) を固定してその後 \(l − 1\) 個のランが連続して現れ、その後 \(0\) が出る確率を考えればよい。

この確率は \(0.8^{k−1} \cdot 0.2\)。よって、求める確率はそれぞれ \(0.2、0.16、0.2 \cdot 0.8^{k−1}\) である。

(4)

求める平均長を \(x\) とすると

\[ \begin{aligned} x &= 0.2\sum_{k=1}^{\infty}k \cdot 0.8^{k-1} \\ 0.8x &= 0.2\sum_{k=1}^{\infty} \cdot 0.8^k \\ &= 0.2\sum_{l=2}^{\infty}(l - 1)\cdot 0.8^{l-1} \\ \end{aligned} \]

両辺の差を取って

\[ \begin{aligned} 0.2x &= 0.2 + 0.2\sum_{k=2}^{\infty}0.8^{k-1} \\ &= 0.2\sum_{k=1}^{\infty}0.8^k = \frac{0.2}{1 - 0.8} = 1 \end{aligned} \]

よって、\(x = 5\) となる。

(5)

求めるエントロピーは

\[ \begin{aligned} &\quad \frac{2}{3}\big(-\frac{9}{10}\log(\frac{9}{10}) - \frac{1}{10}\log(\frac{1}{10})\big) + \frac{1}{3}\big(-\frac{8}{10}\log(\frac{8}{10}) - \frac{2}{10}\log(\frac{2}{10})\big) \\ &= \frac{2}{3}(\log10 - \frac{9}{5}\log3) + \frac{1}{3}(\log10 - \frac{13}{5}) \\ &= \log10 - 1.2 \cdot 1.58 - \frac{13}{15} \\ &= 1 + 2.32 - 1.896 - 0.867 = 3.32 - 2.763 \\ &= 0.557 \end{aligned} \]

(6)

確率 \(\frac{1}{3}\) で \(1\) が発生する際のエントロピーは \(-\frac{1}{3}\log(\frac{1}{3}) - \frac{2}{3}\log(\frac{2}{3}) = \log3 - \frac{2}{3} = 0.913[\text{bit}]\) となり、(5) よりも大きくなる。