東京大学 情報理工学系研究科 電子情報学専攻 2011年度 専門 第5問
Author
Description
離散信号処理に関する以下の問いに答えよ。なお, 離散信号 \(x(n)\) は \(n < 0\) でゼロであるとする。
(1) 離散信号 \(x(n)\) を \(m\) だけシフトさせ \(x(n-m)\) としたとき, この信号の \(z\) 変換が \(z^{-m}X(z)\) となることを示せ。なお, \(X(z)\) は \(x(n)\) の \(z\) 変換である。
(2) \(2\) つの離散信号 \(x_1(n)\) と \(x_2(n)\) のたたみ込み \(x_1(n)*x_2(n)\) の定義を示せ。
(3) \(x_1(n)\) と \(x_2(n)\) の \(z\) 変換がそれぞれ \(X_1(z)\) と \(X_2(z)\) であるとする。(1) と (2) の結果を用いて, \(x_1(n)*x_2(n)\) の \(z\) 変換が \(X_1(z)X_2(z)\) となることを示せ。
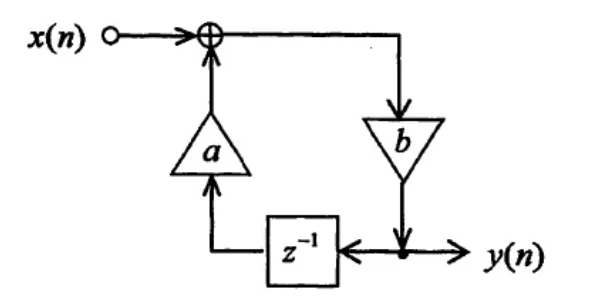
(4) 下図に示す離散時間システムの伝達関数 \(H(z)\) を求めよ。
(5) 離散時間システムインパルス応答の変換は伝達関数と等しくなる。これを用いて, 下図の離散時間システムインパルス応答 \(h(n)\) を求めた上で、離散信号 \(x(n)\) を入力したときの応答 \(y(n)\) を求めよ。
Kai
(1)
\[
\begin{aligned}
X(z) &= \sum_{n=0}^{+\infty}x(n-m)z^{-m} \\
&= \sum_{l=-m}^{+\infty}x(l)z^{-l-m} \\
&= z^{-m}\sum_{l=-m}^{+\infty}x(l)z^{-l} \\
&= z^{-m}x(z)
\end{aligned}
\]
(2)
\(x_1(n)*x_2(n) = \sum_{m=0}^{+\infty}x_1(n-m)x_2(m)\)
(3)
\[
\begin{aligned}
FT \bigg(x_1(n)*x_2(n)\bigg) &= \sum_{n=0}^{+\infty}\sum_{m=0}^{+\infty}x_1(n-m)x_2(m)z^{-n} \\
&= \sum_{m=0}^{+\infty}\sum_{n=0}^{+\infty}X_1(n-m)X_2(m)z^{-n} \\
&= \sum_{m=0}^{+\infty}X_2(m)\sum_{n=0}^{+\infty}X_1(n-m)z^{-(n-m)}\cdot z^{-m} \\
&= \sum_{m=0}^{+\infty}X_2(m)z^{-m}\sum_{n=0}^{+\infty}X_1(n-m)z^{-(n-m)} \\
&= X_1(z)X_2(z)
\end{aligned}
\]
(4)
\[
\begin{aligned}
&b[x(z) + az^{-1}y(z)] = y(z) \\
&bx(z) = (1 - abz^{-1})y(z) \\
&H(z) = \frac{y(z)}{x(z)} = \frac{b}{1-abz^{-1}}
\end{aligned}
\]
(5)
\[
\begin{aligned}
h(n) &= b \cdot (ab)^n = a^n b^{n+1} \\
y(n) &= x(n) * h(n) \\
&= \sum_{k=0}^{+\infty}x(n-k)a^kb^{k+1}
\end{aligned}
\]