東京大学 情報理工学系研究科 コンピュータ科学専攻 2018年2月実施 問題2
Author
Description
For each \(n \geq 1\), let \(\Sigma_n\) be \(\{a_1, \dots, a_n\}\), where \(a_1, \dots, a_n\) are different from each other. For a word \(w \in \Sigma_n^*\), we write \(|w|_{a_i}\) for the number of occurrences of \(a_i\) in \(w\). We define the languages \(L_{\forall, n}\) and \(L_{\exists, n}\) over \(\Sigma_n\) by:
and
Answer the following questions.
(1) Give a deterministic finite state automaton with \(4\) states that accepts \(L_{\forall, 2}\).
(2) Give a non-deterministic finite state automaton with \(7\) states (without \(\epsilon\)-transitions) that accepts \(L_{\exists, 3}\).
(3) Prove that, for every \(n \geq 1\), every deterministic finite state automaton that accepts \(L_{\exists, n}\) has at least \(2^n\) states.
(4) Prove that, for every \(n \geq 1\), every non-deterministic finite state automaton (without \(\epsilon\)-transitions) that accepts \(L_{\forall, n}\) has at least \(2^n\) states.
Kai
(1)
This one was also solved in Automata Theory, Languages and computation 3rd ed, 2.2.4, Example 2.4
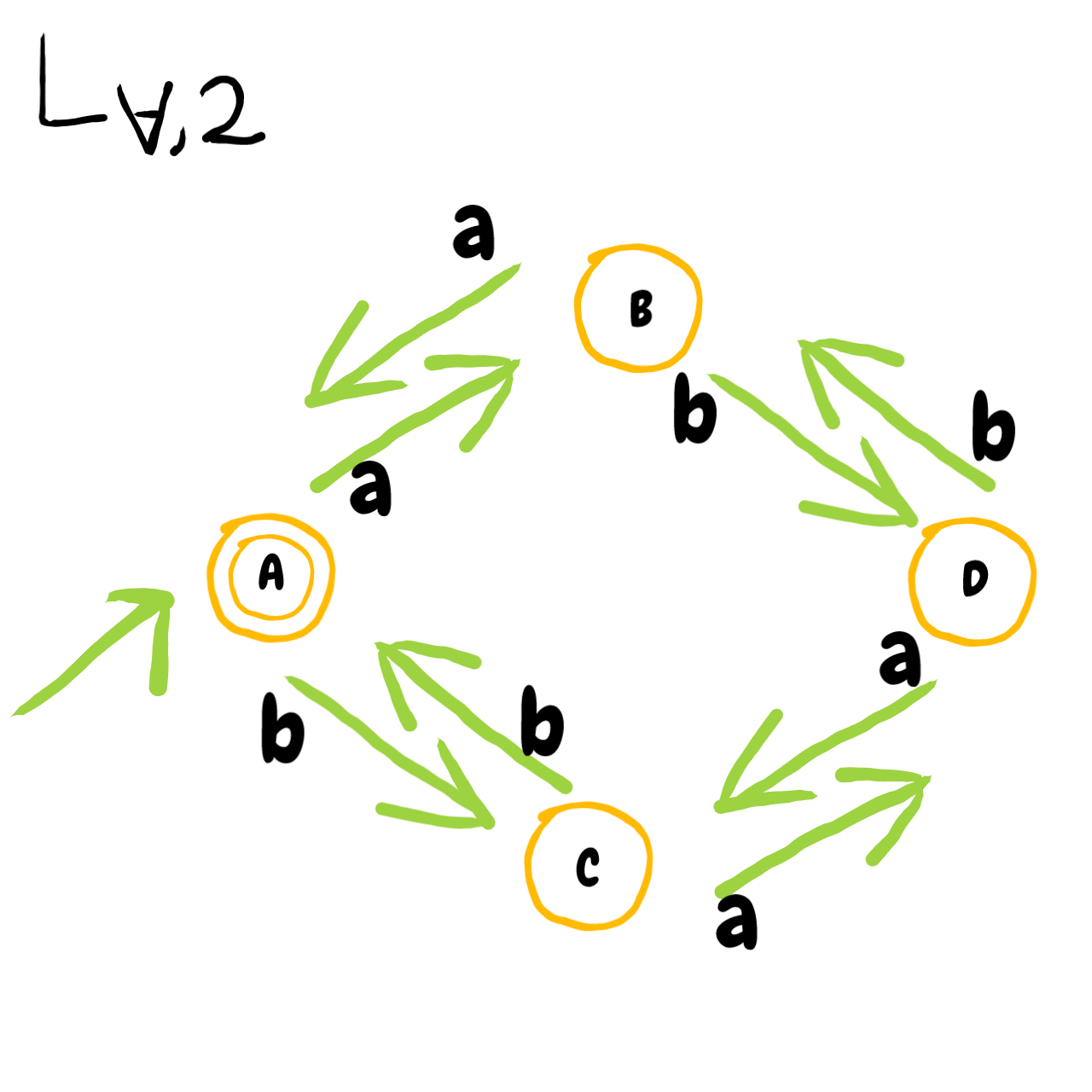
Explanation: - A: "number of \(a\)'s is even, number of \(b\)'s is even" - B: "number of \(a\)'s is odd, number of \(b\)'s is even" - C: "number of \(a\)'s is even, number of \(b\)'s is odd" - D: "number of \(a\)'s is odd, number of \(b\)'s is odd"
(2)
Begin with an \(\epsilon\)-NFA as depiced in Fig. (2-a). It "guesses" which letter appears even number of times. To make it \(\epsilon\)-free, we either follow him: https://youtu.be/sq-dLKAd6bo?t=1714 or consider the followig: starting from start state, how far, i.e. which states can we reach on letter \(a\)? There are \(3\) such states. We simply draw an edge to those states. Do the same for \(b,c\). The final answer is on Fig. (2-b)
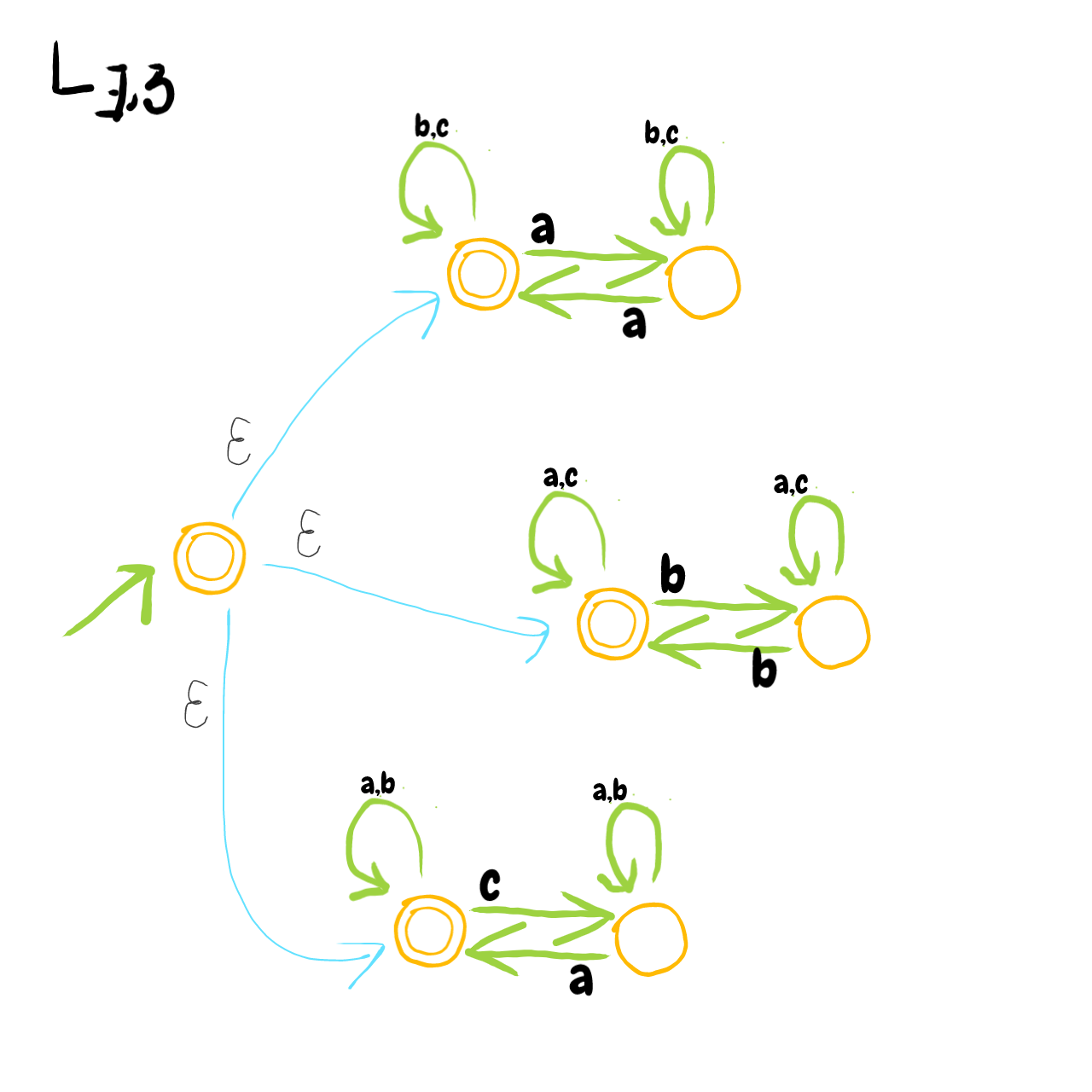
Fig. (2-a)
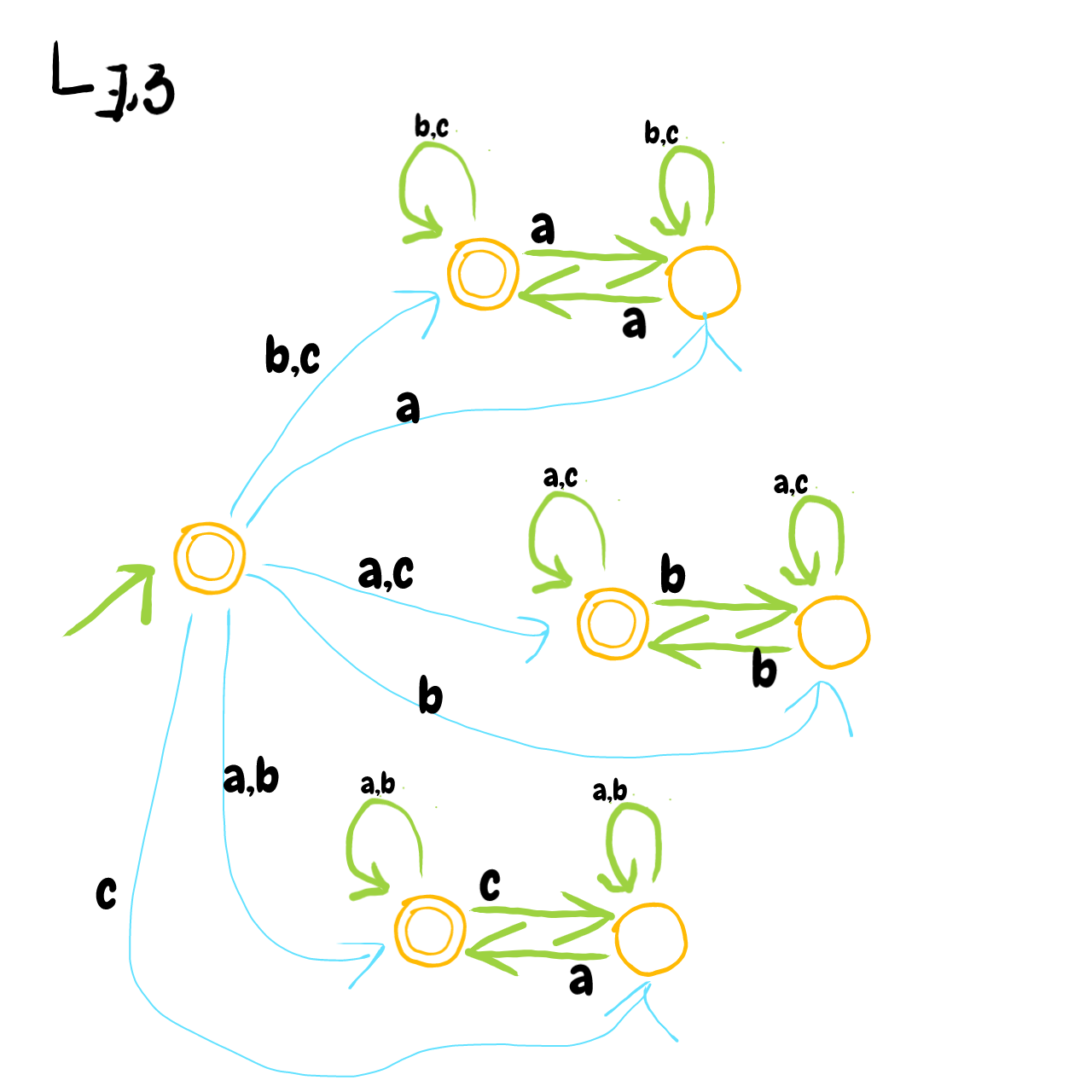
Fig. (2-b)
(3)
Prove that, for every \(n\geq 1\), every deterministic finite state automaton that accepts \(L_{\exists ,n}\) has at least \(2^n\) states.
First, I'll show that there is a DFA with \(2^n\) states. We can encode states of DFA \(L_{\exists ,n}\) as a binary string \(B = (b_n, b_{n-1}, \cdots, b_2, b_1)\) of length \(n\), where \(b_i = 1\) iff numbers of \(a_i\)'s is odd in so-far read sequence, else \(0\). A state is accepting if its binary representation has at least one zero. There are \(2^n\) such strings.
Now, I'll show that there is no DFA with less than \(2^n\) states. If the DFA had fewer than \(2^n\) states, then there would be some state \(q\) such that the DFA can be in state \(q\) after reading two different sequences of length \(n\), say \(a = a_1a_2\cdots a_n\) and \(b = b_1b_2\cdots b_n\). If the sequences were of different parity, i.e. one of the sequences had a letter which appears even number of times, and the other sequence hadn't, then \(q\) would be both accepting and nonaccepting state. If the sequences were of the same parity, then we could append some sequence \(c_1\cdots c_m \in \Sigma^*\) to \(a\) and \(b\) such that \(a_1a_2\cdots a_n c_1\cdots c_m\) and \(b_1b_2\cdots b_n c_1\cdots c_m\) have different parity. Consider state \(p\) that the DFA enters after reading \(c_1\cdots c_m\). Then \(p\) must be both accepting and nonaccepting, since either of \(a_1a_2\cdots a_n c_1\cdots c_m\) and \(b_1b_2\cdots b_n c_1\cdots c_m\) is accepted and the other isn't.
This problem could be also one-lined using Myhill-Nerode theorem. The only one difficulty here is to define \(2^n\) equivalent classes. Try fiddling with binary strings.
(4) - send help
Prove that, for every \(n\geq 1\), every non-deterministic finite state automaton (without \(\epsilon\)-transitions) that accepts \(L_{\forall ,n}\) has at least \(2^n\) states.
Begin with constructing DFA \(A\) accepting \(L_{\forall ,n}\) the same way as in Q3 – except that \(A\) has only one accepting state, a string of all \(0\)'s. Obviously this DFA is also a~NFA. The equivalent NFA simply cannot guess parity of some letters: it has to remember information of parity of each letter. As shown in Q3, every letter requires \(2\) bits, so minimum of \(2^n\) states are required.