東京大学 情報理工学系研究科 コンピュータ科学専攻 2017年2月実施 問題2
Author
Description
For a non-deterministic finite automaton \(M\) over an alphabet \(\Sigma\), we write \(\mathcal{L}(M) \subseteq \Sigma^*\) for the set of words accepted by \(M\). We write \(|w|\) for the length of the word \(w\), and write \(\mathbb{N}\) for the set of non-negative integers.
Answer the following questions:
(1) Consider the non-deterministic finite automaton \(M_0\) depicted below, where \(q_0\) is the start state, and \(q_3\) is the only final state. Give \(x, y, z \in \{a, b, c\}^*\) that satisfy all of the following conditions:
- (i) \(xyz = abcc\)
- (ii) \(|y| > 0\)
- (iii) \(x y^n z \in \mathcal{L}(M)\) for every \(n \in \mathbb{N}\).
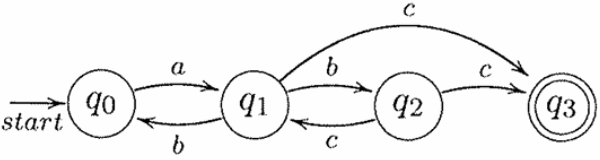
(2) Prove that, for every non-deterministic finite automaton \(M\) consisting of \(k\) states and for every \(w \in \mathcal{L}(M)\) such that \(|w| \ge k\), there exist \(x, y,\) and \(z\) that satisfy all of the following conditions:
- (i) \(xyz = w\)
- (ii) \(|y| > 0\)
- (iii) \(|xy| \le k\)
- (iv) \(x y^n z \in \mathcal{L}(M)\) for every \(n \in \mathbb{N}\).
(3) Prove that there exists no non-deterministic finite automaton \(M\) such that \(\mathcal{L}(M) = \{ a^m b^n \mid m, n \in \mathbb{N}, 0 < m < n \}\). You may use the fact proved in question (2).
Kai
(1)
\(x = a\), \(y = bc\) and \(z = c\)
(2)
Classic proof of Pumping Lemma (PL) for regular languages. Let \(\mathcal{M}\) be an automaton with \(k\) states. Let \(w = a_1a_2\cdots a_k \in L(M)\) such that \(|w| > k\). Now let's simulate run of \(\mathcal{M}\) of word \(w\). Define states \(p_i = \hat\delta(q_0, w_1w_2\cdots w_i)\). That is, \(p_i\) is a state in which \(\mathcal{M}\) is after reading first \(i\) inputs. From pigeonhole principle, at lest two of those state must be exactly the same state. Let \(p_i = p_j\) be the state that is visited the second time for the first time (i.e. \(i\) is the smallest among all such states).
I claim that: \(w = xyz\), where
- \(x = a_1a_2\cdots a_{i-1}\)
- \(y = a_ia_{i+1}\cdots a_{j-1}\)
- \(z = a_ja_{j+1}\cdots a_k\)
Obviously, \(|y| > 0\) because \(i\neq j\) and \(|xy| = j - 1 \leq n\). States \(p_i, \dots, p_j\) create a loop in the automaton - it can be traversed any number of times, thus \(xy^nz \in L(\mathcal{M})\). For \(n=0\) we simply "skip" the loop, for \(n\geq 1\) we traverse the loop \(n\) times.
(3)
\(L(M) = \{ a^m b^n | n,m \in \mathbb{N}, 0<m<n \}\) Assume that \(L\) is regular language. Then pumping lemma must hold. Consider \(w = a^k b^{k+1} \in L\), where \(k\) is the pumping lemma constant. Because \(|w| = 2k + 1 > k\), then there must exist a partitioning \(xyz = w\) such that \(|xy| < k\), \(|y|>0\) and \(xy^nz \in L\) \textbf{for all} \(n\in\mathbb{N}\). Notice that \(xy\) consists of \(a\)'s only. Let's "pump up" \(y\). For example, \(xy^{42}z\) contains of significantly more \(a\)'s than \(b\)'s. This word does not belong to the language. Contradiction with statement that \(x y^n z \in L\) for all \(n\in N\). \(L(M)\) is not regular, thus there exist no automaton recognizing it.