東京大学 情報理工学系研究科 コンピュータ科学専攻 2016年2月実施 問題4
Author
Description
The majority gate \(\text{M}_3\) is a binary logic gate defined as follows: \(\text{M}_3\) has \(3\) inputs and \(1\) output. The output is \(1\) if two or three of the inputs are 1; and 0 otherwise.
When you answer circuit designs in the questions below, you can use NOT gates and constants \(0\) and \(1\) in addition to \(\text{M}_3\) gates, but other gates such as AND or OR cannot be used. You should draw an \(\text{M}_3\) gate as a rectangle labeled with \(\text{M}_3\), and a NOT gate as a circle, as shown in the following example:
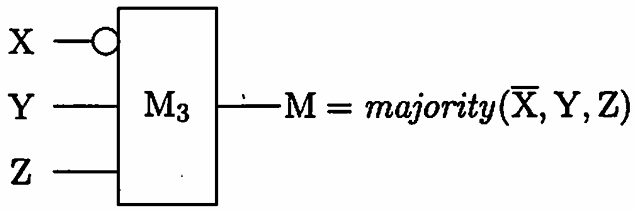
Answer the following questions. Try to make \(\text{M}_3\)-levels (i.e. the maximum number of serially connected \(\text{M}_3\) gates) as small as possible in your answers.
(1) Design and depict the following logic circuits:
- (a) AND of \(2\) inputs,
- (b) OR of \(2\) inputs,
- (\(c\)) XOR of \(2\) inputs.
(2) A 1-bit full adder \(\text{FA}_1\) is defined as follows: \(\text{FA}_1\) has \(3\) inputs and \(2\) outputs called \(\text{S}\) (sum) and \(\text{C}\) (carry), respectively. \(\text{S}\) and \(\text{C}\) are defined so that \(2\text{C} + \text{S}\) is equal to the sum of the \(3\) input bits.
Design and depict a \(1\)-bit full adder \(\text{FA}_1\). Answer its \(\text{M}_3\)-level, too. You can use the circuits you have designed in Question (1).
(3) Design and depict a \(4\)-bit full adder \(\text{FA}_4\). Answer its \(\text{M}_3\)-level, too.
Here \(\text{FA}_4\) takes, as inputs: (i) two unsigned \(4\)-bit integers, and (ii) a carry bit.
It outputs the \(5\)-bit sum. You can use the circuits you have designed in Questions (1) and (2).
(4) Design and depict a \(4\)-bit multiplier \(\text{MUL}_4\). Answer its \(\text{M}_3\)-level, too.
Here \(\text{MUL}_4\) takes two unsigned \(4\)-bit integers as inputs. It outputs the \(8\)-bit product of the inputs. You can use the circuits you have designed in Questions (1), (2), and (3).
Kai
(1)
- OR(\(x, y\)) = \(majority(0, x, y)\)
- AND(\(x, y\)) = \(majority(1, x, y)\)
- XOR(\(x, y\)) = AND( OR(\(x,y\)), NOT( AND(\(x, y\)) ) = \(majority[1, majority(0,x,y) , not\:majority(1, x, y)]\)
XOR is "\(2\)-\(\text{M}_3\)-level".
(2)
Classic \(1\)-bit full adder. Just draw a table and then depict the circuit. Let \(a,b,c_{in}\) be inputs.
\(S\) yields \(4\)-\(\text{M}_3\) level (2x XOR). \(C\) yields \(3\)-\(\text{M}_3\) level (OR with 2-level AND). Thus, \(\text{FA}_1\) has \(4\)-\(\text{M}_3\) level.
Bonus: \(C = majority(c_{in}, a,b)\). Thanks Igor!
(3)
Connect \(4\) \(\text{FA}_1\) in series. It's \(\text{M}_3\) level is \(4\cdot4 = 16\).
(4)
Classic \(4\)-bit multiplier (google for images). Connect three \(4\)-bit adders in series and try not to get messed with connections. \(\text{M}_3\) level is: \(3\cdot 16 + 8\cdot 1\): each of three \(\text{FA}_4\) has level \(16\) and there's one level of \(8\) AND gates preceding \(\text{FA}_4\)'s.