東京大学 情報理工学系研究科 コンピュータ科学専攻 2016年2月実施 問題2

Author

kainoj

Description

Let us consider nondeterministic finite automata with \(\varepsilon\)-transitions (\(\varepsilon\)-NFAs) over the alphabet \(\Sigma = \{a, b\}\). An \(\varepsilon\)-NFA is an NFA that can additionally have "silent" transitions labeled with a fresh symbol \(\varepsilon\). A word \(w \in \Sigma^*\) is accepted by an \(\varepsilon\)-NFA \(M\) if there exists a word \(w' \in (\Sigma \cup \{\varepsilon\})^*\) such that:

1) \(w'\) is accepted by \(M\) (when \(M\) is considered an NFA over the alphabet \(\Sigma \cup \{\varepsilon\}\)); and 2) removing all the occurrences of \(\varepsilon\) in \(w'\) gives rise to \(w\).

The language \(L(M) \subseteq \Sigma^*\) of an \(\varepsilon\)-NFA \(M\) is the set of words accepted by \(M\).

An example of an \(\varepsilon\)-NFA is given below; it is referred to as \(M_1\). Here \(q_0\) is an initial state and \(q_2\) is an accepting state.

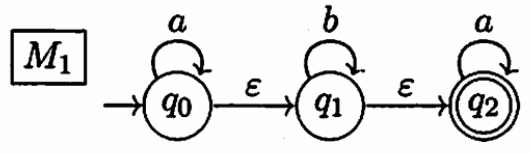
Answer the following questions:

(1) Give a regular expression that designates the language \(L(M_1)\) of the above \(\varepsilon\)-NFA \(M_1\).

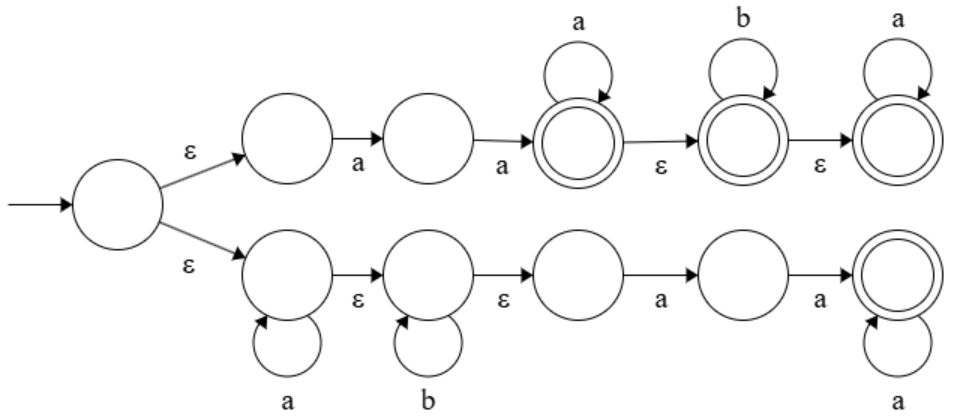
(2) Give an NFA \(M_2\) over \(\Sigma\) such that: \(L(M_2) = L(M_1)\); and \(M_2\) is \(\varepsilon\)-free, that is, there are no transitions labeled with \varepsilon in \(M_2\).

(3) Give an \(\varepsilon\)-NFA \(M_3\) such that

\[ L(M_3) = \{ w \in \Sigma^* \mid w \text{ contains } aa \text{ as a subword, that is, } w = w_1 aa w_2 \text{ for some } w_1, w_2 \in \Sigma^* \}. \]

Your answer may be \(\varepsilon\)-free.

(4) Give an \(\varepsilon\)-NFA \(M_4\) such that \(L(M_4) = L(M_1) \cup L(M_3)\), where \(M_3\) is from Question (3). Your answer may be \(\varepsilon\)-free.

(5) Give an \(\varepsilon\)-NFA \(M_5\) such that \(L(M_5) = L(M_1) \cap L(M_3)\), where \(M_3\) is from Question (3). Your answer may be \(\varepsilon\)-free.

Kai

(1)

\(a^*b^*a^*\)

(2)

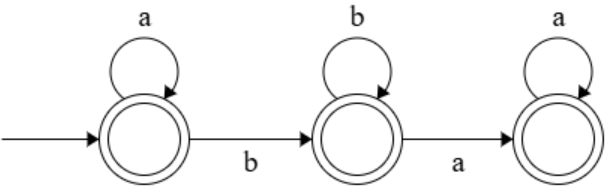
(3)

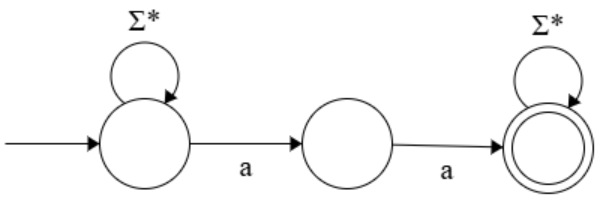
(4)

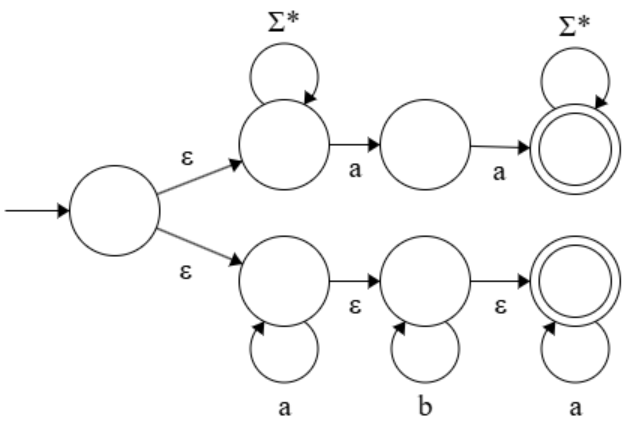
(5)

\(L(M_5)\) contains \(aa\) and is of form of \(aaa^*b^*a^* + a^*b^*aaa^*\).