東京大学 情報理工学系研究科 コンピュータ科学専攻 2015年2月実施 問題2
Author
kainoj, 祭音Myyura
Description
Let us consider nondeterministic finite automata (NFA) and deterministic finite automata (DFA) over the alphabet \(\Sigma = \{a, b\}\). For example, the NFA \(M_1\) shown below
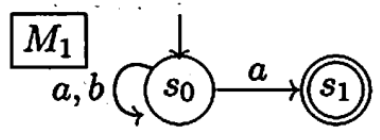
recognizes the language
Here \(\Sigma^*\) denotes the set of words over \(\Sigma\).
Answer the following questions.
(1) Present an NFA, with at most four states, that recognizes the language
Here \(|w|\) denotes the length of the word \(w\).
(2) Present a DFA that recognizes the language \(L_3\) in Question (1).
(3) A DFA that recognizes the language \(L_3\) has no less than \(2^3 = 8\) states. Prove this fact.
(4) Argue for the following statement:
- To recognize the same language, a DFA possibly needs the number of states that is exponentially bigger than an NFA does.
Kai
(1)
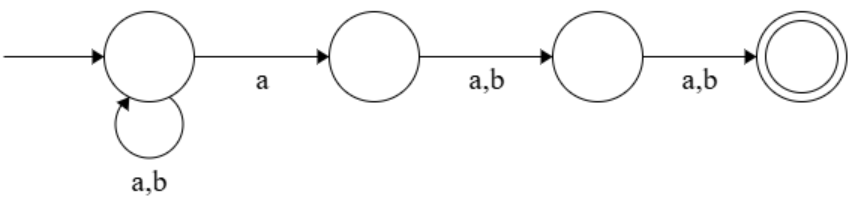
(2)
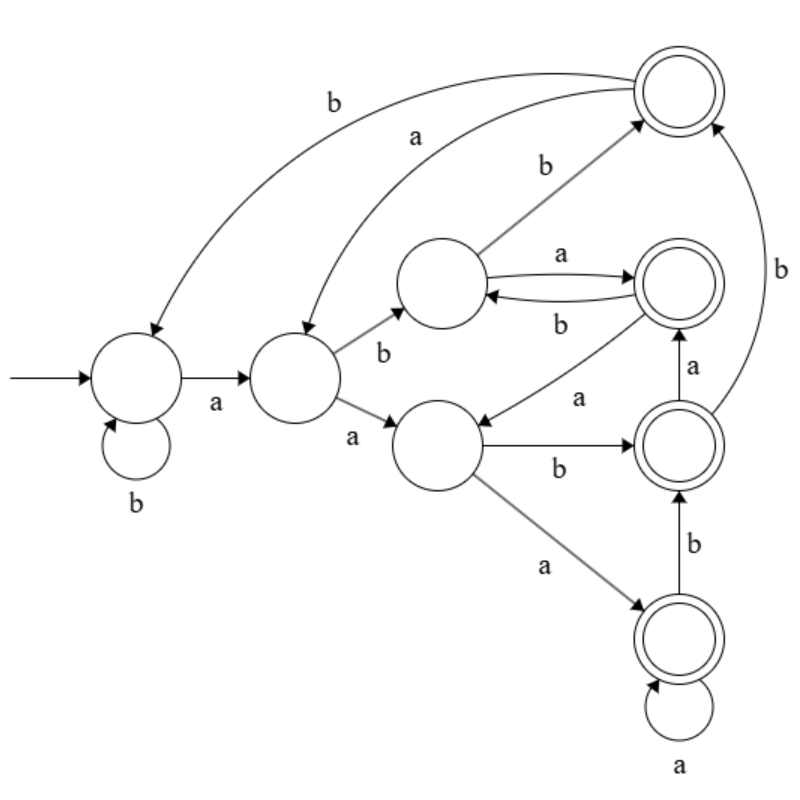
(3) + (4)
I'll prove that DFA that recognizes \(L_n\):
has no less than \(2^n\) states. This is almost a copy-paste from Introduction to Automata Theory, Languages and Computation 3rd ed., Chapter 2.3.6.
Intuitively we need \(2^n\) states to remember every possible ending of length \(n\): we can encode it as a binary string of length \(n\). Now, I'll show that there's no such DFA with less than \(2^n\) states.
Suppose that there's DFA \(D\) recognizing \(L_n\) with less tan \(2^n\) states. If so, then tere must exist a state \(q\) in which \(D\) is after reading two different sequences, say \(x = x_1x_2\cdots x_n\) and \(y = y_1y_2\cdots y_n\). Since they are different, let \(i\in N\) be the last position on which they differ. By symmetry, assume that \(x_i = a\) and \(y_i = b\).
- if \(i = 1\), then \(x = a\:x_2\cdots x_n\) and \(y = b\:y_2\cdots y_n\). Which means that state \(q\) is both accepting and non-accepting.
- if \(i > 1\), then we can append \((n-i)\) \(b\)'s to both \(x\) and \(y\). Then a state \(p\) in which \(D\) is after reading \(ax_{i+1}\cdots x_nb\cdots b\) and \(by_{i+1}\cdots y_nb\cdots b\) is both accepting and non-accepting.
In both cases we get lead to contradiction. Thus, DFA recognizing \(L_n\) has at least \(2^n\) states.
- (3): Let \(n = 3\). Then DFA recognizing \(L_3\) has no less than \(8\) states.
- (4): NFA recognizing \(L_n\) has exactly \(n+1\) states. Equivalent DFA has \(2^n\) states.