Skip to content

東京大学 情報理工学系研究科 創造情報学専攻 2018年8月実施 筆記試験 第2問

Author

tomfluff

Description

太陽光発電システムについて考えよう。ソーラーパネルの維持管理のため、以下のような運用規則が定められているとする。

  • (i) \(n\) 枚のパネルが一つのグループとして維持管理される。
  • (ii) パネルはグループごとに定期的に点検される。
  • (iii) パネルの状態は各グループごとに \(n\) ビットデータとして報告される。

ここで各ビットは対応するパネルに不具合があれば \(1\)、不具合がなければ \(0\) とする。 不具合のあるパネルの数、すなわちビットデータの \(1\) の個数 \(k\) を数える “population count” 問題を考えよう。以下の設問に答えよ。

まず、ソフトウェアによる解法を考えよ。ここでは、\(0 < n \leq 32\)、\(0 \leq k < \log_2 n\) とする。
四則演算、論理演算、シフト演算、および表引きには \(1\) 単位時間かかるとする。単純化のため、インデックスの足し算やループで用いる比較演算の演算時間はゼロとする。

(1) 単純な方式として各ビットの値をチェックし、\(1\) の個数の総和を求める方式が考えられる。この方式の疑似コードを書き、その計算時間を答えよ。

(2) 実際、表引き操作を行うことで上述の方式 (1) を高速化できる。その計算時間を答えよ。

(3) 方式 (1) より高速かつ方式 (2) よりストレージを必要としない方式の擬似コードを示せ。その計算時間を答えよ。

ハードウェアによる解決を考えよう。ここでは、入力はビット列、出力は \(2\) 進数とする。

(4) 入力 \(3\) ビットの population count 論理回路 \(P_3\) の真理値表を書け。AND、OR、NOT ゲートを用いて \(P_3\) を設計せよ。

(5) 入力 \(6\) ビットの population count 論理回路 \(P_6\) を論理回路 \(P_3\) を利用して作成せよ。必要に応じて、追加で AND、OR、NOT ゲートを使っても良い。*

(6) 入力 \(n\) ビットの population count 論理回路 \(P_n\) を考える時、\(n\) が増えると遅延が問題となる。この問題を解決する方法を述べよ。

Kai

(1)

1
2
3
4
5
6
7
k = 0
i = 0
while i < 32:
    k = k + (1 & n) // (2 time units)
    n = n >> 1 // shift to the right (1 time unit)
    i = i + 1
return k

Time complexity would be \(O(n)\) in the general case since we go over every indicator once. In this case since \(0<n\leq 32\) then it will be \(O(1)\). Exact computation time would be \(32\cdot 3=96\) units of time.

(2)

In the case where we use lookup tables we can save the shift operation. This means that the computation time would be: \(32\cdot 2=64\) units of time.

(3)

1
2
3
4
5
6
k = 0
i = 1
while i < 2**32:
    k = k + (i & n) // (2 time units)
    i = i << 1
return k

In this method we take only \(32\cdot 2=64\) units of time as (2) but we use less space than with a lookup table. We took advantage of the loop indicator as the mask for the logical and operation.

(4)

Let us use AND, OR and NOT to define a new gate called XOR.

Using XOR, AND, OR and NOT we will creatre P3 as follows:

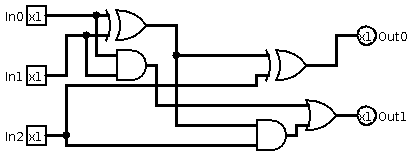
The truth table for it would be:

In0 In1 In2 Out0 Out1
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

(5)

For P6 the logic will be as follows:

(6)

Note: I am not sure about my answer, I think propogation delay is correct but not sure. The question itself isn't clear as well. Should I solve the latency problem or give a reason. Not clear.

Since any of the \(n/3\) elements could contribute to the actual sum, there would be a large number of gates which need the data from the last gates available. That is, there would be many in-line gates which would need to wait for the correct value to propogate forward.