東北大学 理学研究科 地球物理学専攻 2023年度 [7]
Author
Description
(1) 次の微分方程式を解け。なお、問 (ii) は非自明解を求めること。
\[
\begin{aligned}
&\text{(i)} &\frac{dy}{dx} = \frac{y-1}{xy} \\
&\text{(ii)} &\left\{
\begin{aligned}
&\frac{dy_1}{dx} = 6y_1 - 3y_2 - 7y_3 \\
&\frac{dy_2}{dx} = -y_1 + 2y_2 + y_3 \\
&\frac{dy_3}{dx} = 5y_1 - 3y_2 - 6y_3
\end{aligned}
\right.
\end{aligned}
\]
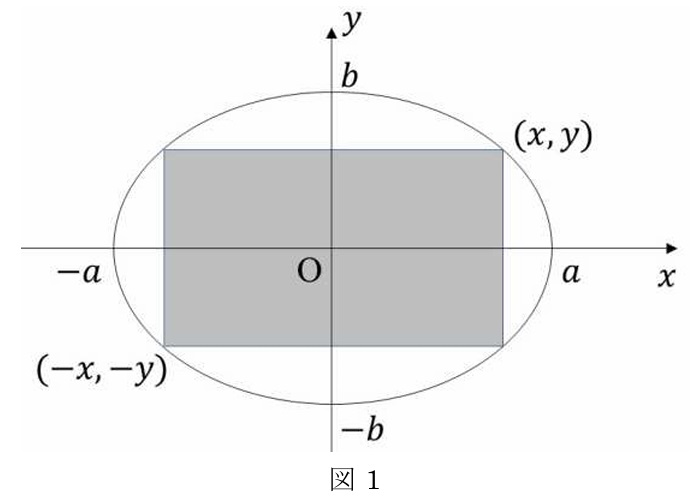
(2) 図1のように長径 \(2a\)、短径 \(2b\) の楕円に内接する長方形の面積の最大値を、ラグランジュの未定乗数法を用いて求めよ。ただし、\(a, b\) は正の定数とする。
(3) \(I \equiv \int_{-\infty}^{\infty} e^{-ax^2}\ \text{d}x\) とするとき、\(I^2 = \frac{\pi}{a}\) であることを示せ。ただし、\(a\) は正の定数とする。
(4) ある部品を使い始めてから故障するまでの時間 \(t\) が指数分布 \(p(t) = \lambda \exp(-\lambda t)\) に従うとする。ただし、\(\lambda > 0\), \(t \ge 0\) とする。
- (i) 部品を使い始めてから時間 \(T\) までに故障が起こらない確率を求めよ。
- (ii) 部品を使い始めてから時間 \(T\) まで故障が起こらなかったと条件の下で、その後、時刻 \(T+\Delta T\) までの間に故障が起こる確率を求めよ。
- (iii) 部品を使い始めてから故障するまでの平均時間を求めよ。
Kai
(1)
(2)
楕円に内接する長方形の頂点の座標を \((x,y)\) ただし \(x,y \gt 0\) とすると、
\[
\begin{align}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\tag{A} \label{A}
\end{align}
\]
が成り立ち、長方形の面積は
\[
\begin{aligned}
S = 4xy
\end{aligned}
\]
である。
そこで、ラグランジュの未定乗数 \(\lambda\) を導入して、
\[
\begin{aligned}
T
&= S - \lambda \left( \frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 \right)
\\
&= 4xy - \lambda \left( \frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 \right)
\end{aligned}
\]
とおき、
\[
\begin{align}
0 &= \frac{\partial T}{\partial x} = 4y - \frac{2 \lambda}{a^2} x
\tag{B} \label{B}
, \\
0 &= \frac{\partial T}{\partial y} = 4x - \frac{2 \lambda}{a^2} y
\tag{C} \label{C}
\end{align}
\]
とおく。
式 (\(\ref{A}\)), (\(\ref{B}\)), (\(\ref{C}\)) から
\[
\begin{aligned}
\lambda = 2ab, \ \
x = \frac{a}{\sqrt{2}}, \ \
y = \frac{b}{\sqrt{2}}
\end{aligned}
\]
が得られるので、求める最大値は
\[
\begin{aligned}
4 \cdot \frac{a}{\sqrt{2}} \cdot \frac{b}{\sqrt{2}}
= 2ab
\end{aligned}
\]
である。
(3)
\[
\begin{aligned}
I^2
&= \int_{-\infty}^\infty e^{-ax^2} dx \int_{-\infty}^\infty e^{-ay^2} dy
\\
&= \int_{-\infty}^\infty dx \int_{-\infty}^\infty dy \ e^{-a(x^2+y^2)}
\\
&= \int_0^{2 \pi} d \theta \int_0^\infty dr \ r e^{-ar^2}
\ \ \ \ \ \ \ \ ( x = r \cos \theta , \ y = r \sin \theta )
\\
&= 2 \pi \left[ - \frac{1}{2a} e^{-ar^2} \right]_0^\infty
\\
&= \frac{\pi}{a}
\end{aligned}
\]
(4)
(i)
時刻 \(T\) までに故障する確率は
\[
\begin{aligned}
F(T)
&= \int_0^T p(t) dt
\\
&= \lambda \int_0^T \exp (- \lambda t) dt
\\
&= - \left[ \exp (- \lambda t) \right]_0^T
\\
&= 1 - \exp (- \lambda T)
\end{aligned}
\]
であるから、求める確率は
\[
\begin{aligned}
1 - F(T)
&= \exp (- \lambda T)
\end{aligned}
\]
である。
(ii)
(i) の \(F\) を使って、求める条件付き確率は次のように計算できる:
\[
\begin{aligned}
\frac{F(T + \Delta T) - F(T)}{1 - F(T)}
&= 1 - \exp ( - \lambda \Delta T )
\end{aligned}
\]
(iii)
\[
\begin{aligned}
\int_0^\infty t p(t) dt
&= \lambda \int_0^\infty t \exp (- \lambda t) dt
\\
&= - \left[ t \exp (- \lambda t) \right]_0^\infty
+ \int_0^\infty \exp (- \lambda t) dt
\\
&= \left[ - \frac{1}{\lambda} \exp (- \lambda t) \right]_0^\infty
\\
&= \frac{1}{\lambda}
\end{aligned}
\]