大阪大学 情報科学研究科 情報工学 2024年度 離散構造
Author
祭音Myyura
Description
本問題で取り扱われるすべてのグラフ (graph) は無向グラフ (undirected graph) であり、多重辺 (parallel edge) や自己ループ (self loop) を持たないものである。グラフ \(G\) は有限 (finite) の頂点集合 (vertex set) \(V\)、および異なる頂点の非順序対 (unordered pair) の集まりである辺集合 (edge set) \(E\) の対 \((V, E)\) と表される。二つのグラフ \(G_1 = (V_1, E_1)\) と \(G_2 = (V_2, E_2)\) が与えられたとき、\(V_1 \neq V_2\) または \(E_1 \neq E_2\) が成立するならば、かつそのときに限り、\(G_1\) と \(G_2\) を異なる (distinct) グラフと見なす。
二つのグラフ \(G_1 = (V_1, E_1)\) および \(G_2 = (V_2, E_2)\) に対して、以下の条件をともに満たす写像 (mapping) \(\varphi: V_1 \rightarrow V_2\) が存在するとき、\(G_1\) と \(G_2\) は同型 (isomorphic) であると呼ぶ。
- \(\varphi\) は全単射 (bijective).
- 任意の \(u, v \in V_1\) について、\(\{u, v\} \in E_1\) ならば、かつそのときに限り \(\{\varphi(u), \varphi(v)\} \in E_2\).
\(\mathcal{G}\) をすべてのグラフの集合 (set) とする。グラフ \(G_1, G_2 \in \mathcal{G}\) が同型であることを, \(\mathcal{G}\) 上の二項関係 (binary relation) を表す記号 \(\simeq\) を用いて \(G_1 \simeq G_2\) と記述するものとする。また、正整数 (positive integer) \(n\) について、\(\mathcal{G}_n\) を頂点集合が \(\{1, 2, \dots, n\}\) であるようなすべてのグラフの集合とする。以下の各問に答えよ。
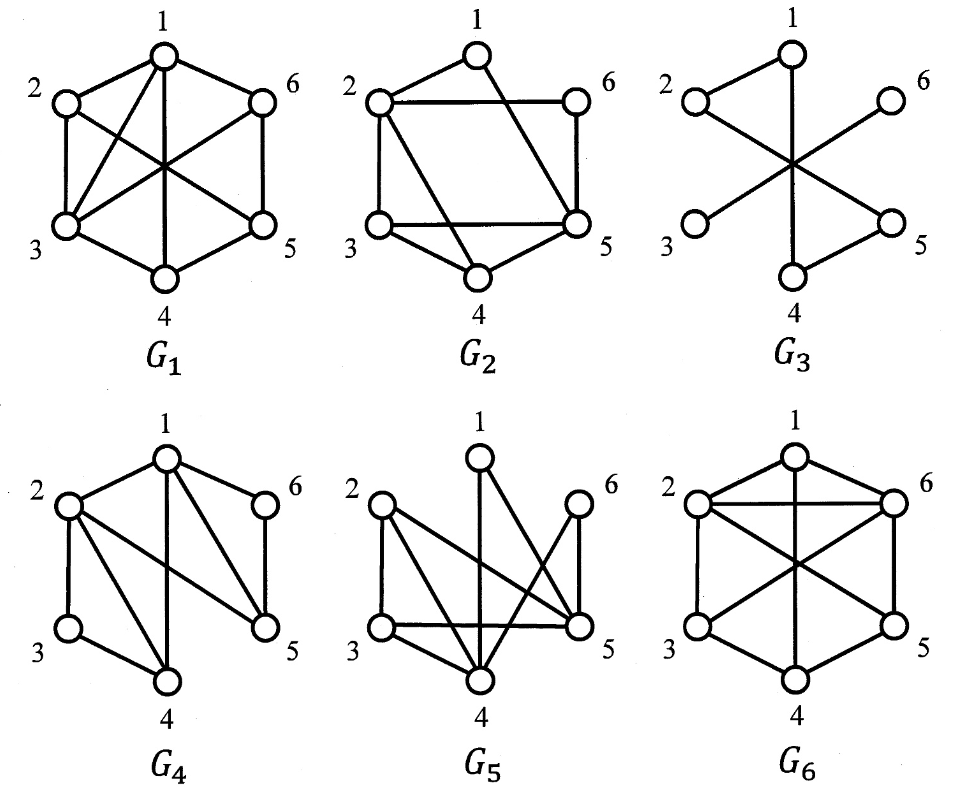
(1) \(\mathcal{H}\) を、以下に図示するグラフ \(G_1, G_2, \dots, G_6\) からなる \(G_6\) の部分集合 (subset) とする。
-
(1-1) \(G_i \simeq G_j\) かつ \(i < j\) を満たす対 (pair) \((i, j)\) をすべて挙げよ。
-
(1-2) \(\simeq\) は同値関係 (equivalence relation) であるため、\(\mathcal{H}\) を \(\simeq\) に基づく複数の同値類 (equivalence class) に分割することができる。それらすべての同値類からなる集合 \(\mathcal{H}/\simeq\) の要素数 (number of elements) を答えよ。
(2) 部分集合 \(\mathcal{I}_n \subseteq \mathcal{G}_n\) を、任意の異なる \(G, H \in \mathcal{I}_n\) について \(G \not\simeq H\) が成立するような部分集合で要素数が最大のものと定義する(もしそのような条件を満たす部分集合が複数ある場合、そのなかの任意の一つが \(\mathcal{I}_n\) として選ばれているものとする)。有限集合 (finite set) \(X\) に対して、記法 \(|X|\) は集合の要素数を表すものとする。
-
(2-1) \(|\mathcal{I}_3|\) の値はいくつになるか。理由とともに答えよ。
-
(2-2) 任意の \(G \in \mathcal{G}_n\) について、高々 \(n!\) 個の異なるグラフ \(G' \in \mathcal{G}_n\) が \(G \simeq G'\) を満たすことを証明せよ。
-
(2-3) \(|\mathcal{G}_n|\) の値はいくつになるか。理由とともに答えよ。
-
(2-4) 以下の不等式 (inequality) が成立することを証明せよ。
Kai
(1)
(1-1)
(1-2)
集合 \(\mathcal{H}/\simeq\) の要素数は \(4\) である。
(2)
(2-1)
\(\mathcal{G}_3\) に属する全てのグラフを検証し、\(V_3 = \{1, 2, 3\}\) とおくと
が分かるから、\(|\mathcal{I}_3| = 4\) である。
(2-2)
同型の定義によれば、\(G = (V, E)\) と \(G' = (V, E')\) が同型である場合、全単射 \(\varphi: V \to V\) が存在し、\(\{u, v\} \in E \iff \{\varphi(u), \varphi(v)\} \in E'\) である。 この全単射は頂点のある順列と考えられ、頂点数が \(n\) のとき、頂点の順列の総数は \(n!\) であるので、\(G\) と同型である \(n\) 個の頂点を持つグラフ \(G'\) は高々 \(n!\) 個である。
(2-3)
グラフ \(G \in \mathcal{G}_n\) は \(n\) 個の頂点を持ち、枝の総数は高々 \(\tbinom{n}{2} = \frac{n(n-1)}{2}\) 本である。 単純グラフは自己ループや多重辺を持たないため、各枝は存在するかしないかの2つの選択肢があり、異なるグラフ全体の総数は \(2^{\frac{n(n-1)}{2}}\) である。
(2-4)
(2-2)、(2-3) より
である。