Skip to content

大阪大学 情報科学研究科 情報工学 2023年度 離散構造

Author

祭音Myyura

Description

グラフ (graph) \(G = (V, E)\) は、 \(n\) 個の頂点 (vertex) の集合 \(V = \{ v_1, v_2, ..., v_n \}\) と、頂点のペアにより定義される辺 (edge) の集合 \(E\) により構成される無向グラフ (undirected graph) である。 また、グラフ \(G\) は同じ頂点を結ぶ辺を持たず、かつ、任意の2つの頂点間を結ぶ辺は高々一つであるとする。

頂点 \(v_i\) と \(v_j\) の間に辺が存在するとき、頂点 \(v_i\) と \(v_j\) は隣接する (adjacent) と呼ぶ。 次の規則で定義される \((i, j)\) 成分 \(a_{ij}\) を持つ \(n \times n\) 行列 \(A_G\) をグラフ \(G\) の隣接行列 (adjacency matrix) と呼ぶ。

\[ a_{ij} = \begin{cases} 1 & (v_i と v_j の間に辺が存在する) \\ 0 & (その他のとき) \end{cases} \]

また、隣接する頂点の系列 \(v_{x_0} \to v_{x_1} \to \cdots \to v_{x_h} \to \cdots \to v_{x_m}\) (\(0 \leq h \leq m\), \(1 \leq x_h \leq n\)) を、長さ \(m\) の歩道 (walk) と呼ぶ。 歩道は同じ頂点を複数含んでも良い。 例えば、下図グラフ \(G_1\) において、 \(v_1 \to v_2 \to v_4 \to v_2 \to v_3\) は長さ 4 の歩道である。

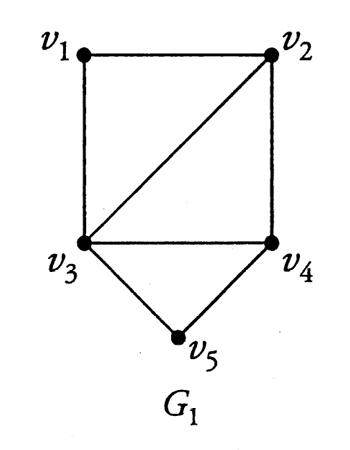
以下の各問に答えよ。

(1) 上図グラフ \(G_1\) の隣接行列 \(A_{G_1}\) を示せ。

(2) グラフ \(G\) における、頂点 \(v_i\) から \(v_j\) の長さ \(k\) (\(k \geq 1\)) の歩道の総数を、\(f_G(k, i, j)\) で表すこととする。

  • (2-1) 上図グラフ \(G_1\) について考える。グラフ \(G_1\) において、\(f_{G_1}(3, 3, 2)\) の値を答えよ。
  • (2-2) 上図グラフ \(G_1\) において、\(\sum_{1 \leq k \leq 3} f_{G_1}(k, 4, 3)\) の値を答えよ。
  • (2-3) グラフ \(G\) における隣接行列 \(A_G\) の \(k\) 乗を \(A_G^k\) で表す。行列 \(A_G^k\) の \((i, j)\) 成分を \(a_{ij}^{(k)}\) と表現すると、\(a_{ij}^{(k)} = f_G(k, i, j)\) になることを証明せよ。

(3) 頂点数が \(n\) の完全グラフ (complete graph) を \(K_n\) とする。

  • (3-1) 完全グラフ \(K_n\) の辺の数を \(n\) を用いて示せ。
  • (3-2) 一般に、\(n \geq 3\) のグラフが \(K_3\) を含むかどうかは、隣接行列を用いて判定することができる。隣接行列 \(A_G\) の \((i, j)\) 成分を \(a_{ij}\), \(A_G^2\) の \((i, j)\) 成分を \(b_{ij}\) としたときに、\(a_{ij}\) と \(b_{ij}\) を用いて、グラフ \(G\) が \(K_3\) を含むかどうかを判定する方法を理由とともに説明せよ。

(4) \(n \ge 2\) のグラフ \(G\) が連結である (connected) とは、行列 \(\boxed{\ \ \ \alpha\ \ \ }\) がそのいずれかの成分にも 0 を持たないことを調べることで確認できる。\(I_n\) を \(n \times n\) の単位行列 (identity matrix) としたときに、隣接行列 \(A_G\), \(I_n\), \(n\) を用いて空間の \(\alpha\) を示せ。

Kai

(1)

\[ A_{G_1} = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 \end{pmatrix} \]

(2)

(2-1)

\[ \begin{aligned} v_3 \to v_2 \to v_3 \to v_2 \\ v_3 \to v_2 \to v_1 \to v_2 \\ v_3 \to v_2 \to v_4 \to v_2 \\ v_3 \to v_1 \to v_3 \to v_2 \\ v_3 \to v_4 \to v_3 \to v_2 \\ v_3 \to v_5 \to v_3 \to v_2 \\ v_3 \to v_5 \to v_4 \to v_2 \end{aligned} \]

よって、\(f_{G_1}(3, 3, 2) = 7\) である。

(2-2)

\(\sum_{1 \leq k \leq 3} f_{G_1}(k, 4, 3) = 10\)

(2-3)

行列 \(A_G\) を二乗したとき、その \((i, j)\) 成分 \(a_{ij}^{(2)}\) は、次のように計算される

\[ a_{ij}^{(2)} = (A_G^2)_{ij} = \sum_{t} a_{it} a_{tj} \]

ここで、\(a_{it} a_{tj} \neq 0\) となるのは \(a_{it} = a_{tj} = 1\) の時のみである。 隣接行列の定義より、頂点 \(v_i\) から \(v_t\) への辺が存在し、かつ、頂点 \(v_t\) から \(v_j\) への辺が存在することがわかる。 よって、長さ 2 の歩道 \(v_i \to v_t \to v_j\) が存在する。

従って、\(a_{ij}^{(2)}\) は、全ての可能な中間頂点 \(v_t\) を通って \(v_i\) から \(v_j\) への長さ 2 の歩道の個数となることがわかる、すなわち、\(a_{ij}^{(2)} = f_{G}(2, i, j)\) である。

次に、\(a_{ij}^{(k-1)}\) は頂点 \(v_i\) から \(v_j\) の長さ \(k-1\) の歩道の総数を表すと仮定する。

同様に、\(a_{ij}^{(k)}\) は、次のように計算すると、

\[ a_{ij}^{(k)} = (A_G^k)_{ij} = (A_G^{k-1}A_G)_{ij} = \sum_{t} a_{it}^{(k-1)} a_{tj} \]

\(a_{ij}^{(k)}\) は頂点 \(v_i\) から \(v_j\) の長さ \(k\) の歩道の個数となることがわかる。

(3)

(3-1)

\[ \frac{n(n-1)}{2} \]

(3-2)

以下の条件を満たす \(i, j, k\) が存在するとき、

\[ a_{ij} = 1, a_{ik} = 1, a_{jk} = 1 \]

グラフ \(G\) が完全グラフ3 \((V=\{v_i, v_j, v_k\}, E=\{v_iv_j, v_iv_k, v_jv_k\})\) を含むから、各成分 \((i, j)\) について、

\[ a_{ij} = 1 \text{ かつ } b_{ij} \ge 2 \]

であるかどうかをチェックすれば、グラフ \(G\) が \(K_3\) を含むかどうかはわかる。

(4)

(The idea is to check the value of \(a_{ij}^{(k)}\) for each \(k \in \{1, 2, \ldots, n-1\}\))

\[ A_G + A_G^{2} + \cdots + A_G^{n-1} \]

or

\[ (I_n + A_G)^{n-1} \]