Skip to content

名古屋大学 情報学研究科 情報システム学専攻 2022年8月実施 専門 問5

Author

祭音Myyura

Description

配列を利用してヒープを実現し，優先度付きキューとして使用することを考える． 取り扱うデータは整数であると仮定し，データの値そのものをヒープのキーとして使用する． ヒープは，最下層のみに節点の欠落を許す完全2分木として構成し，最下層の節点は左側から詰めて配置する． ヒープの根節点を節点 1，節点 i の左右の子をそれぞれ節点 2i, 節点 2i+1 と呼ぶ． 内部節点 i のキーの値は，その子 2i および 2i+1 のキーの値以上となっている必要があり，これをヒープ条件という．

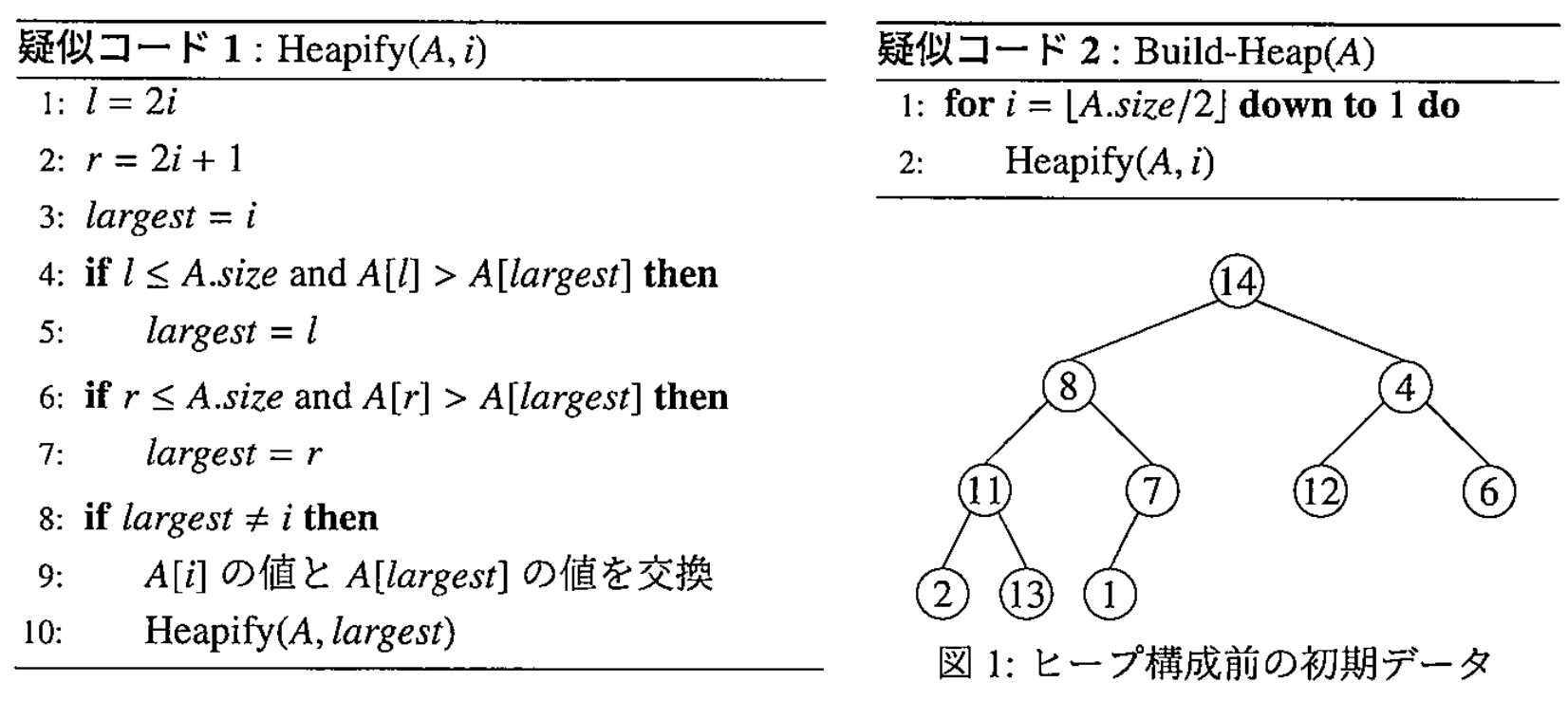
十分大きなサイズを持つ配列 A の存在を仮定し，ヒープにおける節点 i のデータを配列要素 A[i] に格納する． また，配列 A の中に格納されているデータ数（ヒープの節点数）を変数A.size に代入して記録する（したがって，ヒープのデータは A[1], ..., A[A.size]に格納されている）． 疑似コード1の Heapify は節点 i で局所的に崩れたヒープ条件を修復する操作，疑似コード 2 の Build-Heap は全ての節点でヒープ条件が成り立つようデータを移動する操作である． なお，\(\lfloor x \rfloor\) は \(x\) 以下の最大整数を表す．

(1) 配列 A の中に，図 1 に示すようなデータが格納されている．この図に対応する配列要素 A[1], ..., A[10] の値を示せ．

(2) 問 (1) の配列 A に対し Build-Heap(A) を実行した後のヒープを，図 1 のような2分木として示せ．

上記のように実現したヒープを利用し，優先度付きキューを構成する． 優先度付きキューから最大のデータを取り出す Pull 操作，優先度付きキューにデータ（キー）を挿入する Push 操作は，疑似コード 3,4 のように実現される．

(3) 疑似コード 3 で (X) となっている箇所に記載すべき操作を，1 行の疑似コードとして示せ． 複数の疑似コードが考えられる場合は，できるだけ効率の良いものを解答すること．

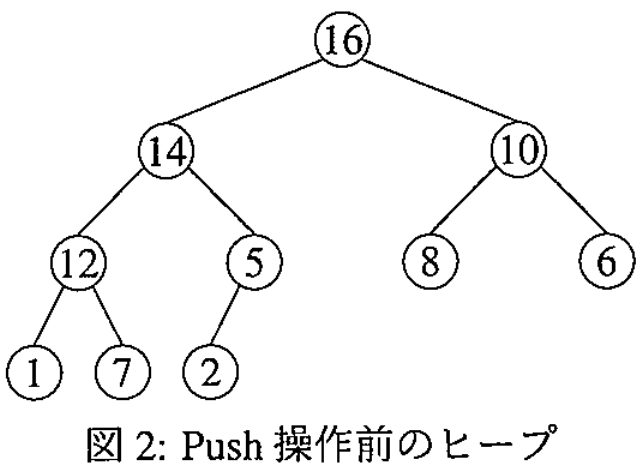
(4) 図 2 のヒープが配列 A に格納されているとする．このとき，Push(A,15) を実行した後のヒープを2分木として示せ．

優先度付きキューに格納されているデータ数（ヒープの節点数）を n とする．

(5) Push の最悪時間計算量を n に関するオーダー記法で示せ．また，その計算量となる理由を説明せよ．

(6) Build-Heap の最悪時間計算量を　n　に関するオーダー記法で示せ．また，その計算量となる理由を説明せよ．

Kai

(1)

1
A = [14, 8, 4, 11, 7, 12, 6, 2, 13, 1]

(2)

1
2
3
4
5
6
7
                             14
                        /          \
                       13           12
                    /      \      /    \
                  11        7    6      4
                /    \     /
               2      8   1

(3)

Heapify(A, 1)

(4)

1
2
3
4
5
6
7
                             16
                        /          \
                       15           10
                    /      \      /    \
                  12        14   8      6
                /    \     /   \
               1      7   2     5

(5)

最悪のとき、while 文の実行する回数が \(\log (\text{A.size})\) なので、Push の最悪時間計算量は \(O(\log n)\) となる。

(6)

Build-Heap の最悪時間計算量を \(T(n)\) とおくと、

\[ \begin{aligned} &T(n) = \underbrace{0 \times \frac{n}{2}} \quad + \quad \underbrace{1 \times \frac{n}{4}} \quad + \cdots + \quad \underbrace{\log (n-1) \times 1} \\ &(i =\lfloor n/2 \rfloor \sim n \quad\lfloor n/4 \rfloor \sim \lfloor n/2 \rfloor \qquad \qquad \qquad \ \ 1 \qquad \ \ ) \end{aligned} \]

よって、

\[ \begin{aligned} T(n) &= n \sum_{k=0}^{\log (n-1)} \frac{k}{2^{k+1}} \\ T(n) &= n \sum_{k=0}^{h} \frac{k}{2^{k+1}} \quad (h = \log (n-1)) \\ 2T(n) &= n \sum_{k=0}^{h} \frac{k}{2^{k}} \\ 2T(n) - T(n) &= n (\frac{1}{2} + \frac{1}{4} + \cdots + \frac{1}{2^h} - \frac{h}{2^{h+1}}) \\ & \leq n ( 2 - \frac{h}{2^{h+1}}) = O(n) \end{aligned} \]