Skip to content

名古屋大学 情報学研究科 情報システム学専攻 2021年8月実施 専門 問1

Author

祭音Myyura

Description

頂点と辺からなり、各辺に距離が与えられている無向グラフに対して、頂点間の最短経路を求めるプログラムを考える。

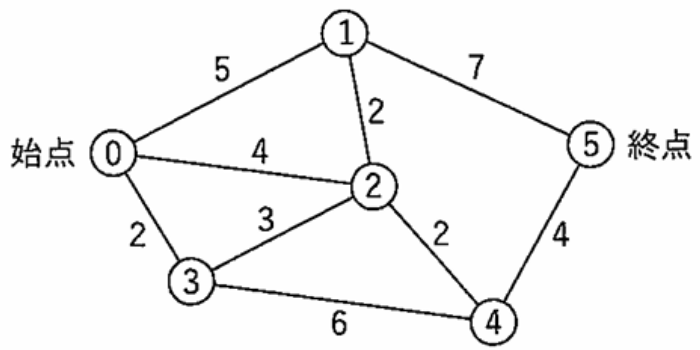
プログラム 1 は、下図に示すグラフの始点から終点までの最短経路とその距離を出力する C 言語プログラムである。 グラフの構造は、配列 graph.data に格納されている。 配列の各要素が各辺に対応しており、要素を構成する3つの数値は、辺の両端の頂点と距離を表している。なお、プログラムの行頭の数字は行番号を表す。

このプログラムを実行すると、次のような出力が得られる。

1
2
total distance: 10
shortest path: 0 -> 2 -> 4 -> 5

このプログラムに関して、以下の問いに答えよ。

(1) 空欄 [ A ], [ B ], [ C ] を埋めて、プログラムを完成させよ。

(2) このプログラムを実行すると、61 行目の代入文は何回実行されるか答えよ。

(3) このプログラムを次のように変更した場合の出力を答えよ。なお、それぞれの変更は個別に行うものとする。

  • (a) 16行目の { 0, 2, 4 } を、{ 0, 2, 6 } に変更した場合
  • (b) 20行目の { 2, 4, 2 } を、{ 2, 4, 5 } に変更した場合

(4) このプログラムが "error!" を出力するのは、与えるグラフ(graph.dataの値)がどのような構造になっている場合か答えよ。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <stdio.h>

typedef struct {
    int node1;
    int node2;
    int distance;
} EDGE;

#define NUM_NODE    6
#define NUM_EDGE    9
#define START_NODE  0
#define END_NODE    5

const EDGE graph_data[NUM_EDGE] = {
    { 0, 1, 5 },
    { 0, 2, 4 },
    { 0, 3, 2 },
    { 1, 2, 2 },
    { 2, 3, 3 },
    { 2, 4, 2 },
    { 3, 4, 6 },
    { 4, 5, 4 },
    { 1, 5, 7 },
};

typedef struct {
    int total_distance;
    int previous_node;
} NODE;

NODE node_stat[NUM_NODE];

#define UNKNOWN         -1
#define LARGE_DISTANCE  10000

void print_path(int node)
{
    if (node != START_NODE) {
        [ 空欄 A ];
        printf(" -> %d ", node);
    }
    else {
        printf("shortest path: %d", node);
    }
}

int main()
{
    int i, j;
    int min_src_node, min_dst_node, min_distance;
    int node1, node2, distance, new_distance;

    for (i = 0; i < NUM_NODE; i++) {
        node_stat[i].total_distance = UNKNOWN;
    }
    node_stat[START_NODE].total_distance = 0;

    while (1) {
        min_distance = LARGE_DISTANCE;
        for (j = 0; j < NUM_EDGE; j++) {
            node1 = graph_data[j].node1;
            node2 = graph_data[j].node2;
            distance = graph_data[j].distance;

            if (node_stat[node1].total_distance != UNKNOWN) {
                if (node_stat[node2].total_distance == UNKNOWN) {
                    new_distance = node_stat[node1].total_distance + distance;
                    if (new_distance < min_distance) {
                        min_distance = new_distance;
                        min_src_node = node1;
                        min_dst_node = node2;
                    }
                }
            }
            else {
                if (node_stat[node2].total_distance != UNKNOWN) {
                    new_distance = node_stat[node2].total_distance + distance;
                    if (new_distance < min_distance) {
                        min_distance = new_distance;
                        min_src_node = [ 空欄 B ];
                        min_dst_node = [ 空欄 C ];
                    }
                }
            }
        }
        if (min_distance == LARGE_DISTANCE) break;
        node_stat[min_dst_node].total_distance = min_distance;
        node_stat[min_dst_node].previous_node = min_src_node;
    }

    if (node_stat[END_NODE].total_distance == UNKNOWN) {
        printf("error!");
    }
    else {
        printf("total distance: %d\n", node_stat[END_NODE].total_distance);
        print_path(END_NODE);
    }
    printf("\n");
}

Kai

プログラム１は、ベルマン・フォード法 (Bellman–Ford algorithm) を実装したＣ言語プログラムである。

(1)

  • [ 空欄 A ]: print_path(node_stat[node].previous_node)
  • [ 空欄 B ]: node2
  • [ 空欄 C ]: node1

(2)

54 回。

（ヒント：ベルマン・フォード法の計算量を考える）

(3)

(a)

1
2
total distance: 11
shortest path: 0 -> 3  -> 2  -> 4  -> 5

(b)

1
2
total distance: 12
shortest path: 0 -> 3  -> 4  -> 5

(4)

始点から終点までの経路が存在しない場合。