九州大学 システム情報科学府 情報理工学専攻・電気電子工学専攻 2024年度 解析学・微積分
Author
Casablanca
Description
(1) 積分
\[
I = \int_{0}^{\infty}x^5\exp(-x^4)dx
\]
を計算せよ。ただし, \(\int_{-\infty}^{\infty}\exp(-x^2)dx = \sqrt{\pi}\) を証明なしに用してよい。
(2) 次の微分方程式の一般解を求めよ。
\[
\frac{dy}{dx} + y = x\sinh x
\]
(3) 複素関数 \(f(z) = \frac{1}{z^4 + 1}\) を考える。次の各問いに答えよ。
-
(a) \(f(z)\) の極をすべて求めよ。
-
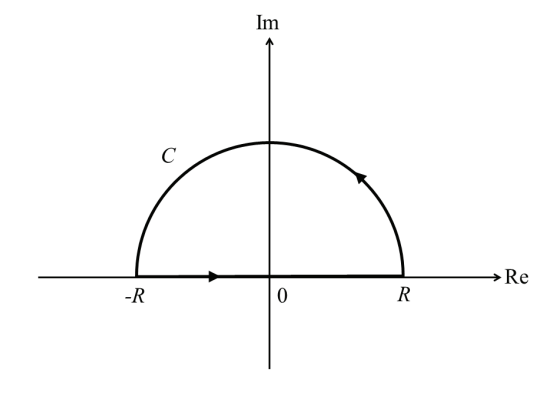
(b) 下図に示す半円 \(C\) に沿った複素積分 \(\oint_{C}f(z)dz\) を求めよ。ただし, \(R > 1\) とする。
Kai
(1)
\[
\begin{aligned}
% (\int_{-\infty}^{\infty}e^{-x^2}dx)^2 &= \int e^{-x^2}dx \int e^{-y^2}dy = \int e^{-(x^2+y^2)dxdy} = \pi \\
\left(\int_{-\infty}^{\infty}e^{-x^2}dx \right)^2 &= \pi \\
\int x^5 e^{-x^4}dx &= \int-\frac{x^2}{4}de^{-x^4} = -\frac{1}{4}x^2e^{-x^4} + \frac{1}{4}\int e^{-x^4}dx^2 \\
\int_0^{\infty}x^5 e^{-x^4}dx &= \frac{1}{4}\int_0^{\infty}e^{-t^2}dt = \sqrt{\pi}/8
\end{aligned}
\]
(2)
\[
\begin{aligned}
\frac{dy}{dx} + y &= x(e^x - e^{-x})/2 \\
e^x(y' + y) &= \frac{1}{2}x(e^{2x} - 1) \\
(e^x y)' &= \frac{1}{2}xe^{2x} - \frac{1}{2}x \\
\int (\frac{1}{2}xe^{2x} - \frac{1}{2}x)dx &= \frac{1}{4}xe^{2x} - \frac{1}{8}e^{2x} - \frac{x^2}{4} + C,
\end{aligned}
\]
\[
y = \frac{1}{4}xe^x - \frac{1}{8}e^x - \frac{1}{4}x^2e^{-x} + C
\]
where \(C\) is a constant.
(3)
(a)
Consider \(z^4 = -1\),
we get
\[
z_1 = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i , z_2 = \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}i , z_3 = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i , z_4 = -\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}i
\]
and these are the poles
(b)
\[
\begin{aligned}
\oint_Cf(z)dz &= 2\pi i \text{Res}[f(z),\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i] + 2\pi i \text{Res}[f(z),\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i] \\
&= \frac{\sqrt{2}}{2}\pi
\end{aligned}
\]