九州大学 システム情報科学府 情報理工学専攻・電気電子工学専攻 2020年度 解析学・微積分
Author
Yu
Description
微分方程式
関数 \(y(x)\) の微分方程式
\[
(x^4 - 1)\frac{\text{d}y}{\text{d}x} = y^2 + 2x^3y - 3x^2
\]
について以下の問いに答えよ.
(1) 与えられた微分方程式は,\(y_p(x) = ax^3\) の形の特殊解を持つ.\(y_p(x)\) を求めよ.ただし \(a\) は定数とする.
(2) 特殊解 \(y_p(x)\) と関数 \(u(x)\) を用いて \(y = y_p + \frac{1}{u}\) とおき,一般解を求めよ.
複素関数論
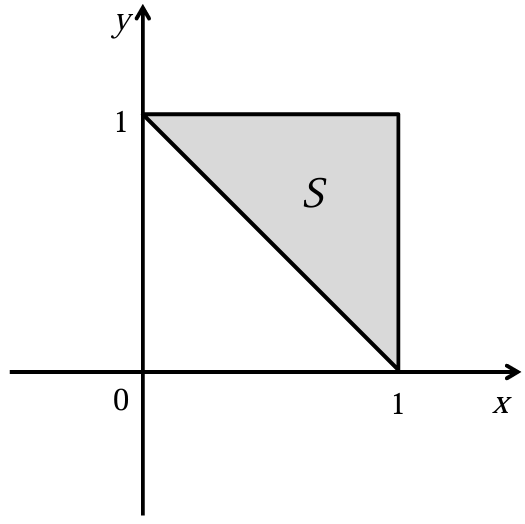
図に示す \(z\) 平面における \(x = 1, y = 1, y = 1 − x\) で囲まれた三角領域 \(S\) を考える.以下の変 換で \(S\) が写像される \(w\) 平面の領域 \(S'\) を図示すると共に、 \(S'\) を囲む境界の方程式を示せ.ただし,\(z = x + iy,w = u + iv\) は複素数,\(x, y, u, v\) は実数,\(i = \sqrt{-1}\) である.
(1) \(w = z + (1 - \sqrt{3}i)\)
(2) \(w = 2e^{\frac{\pi i}{6}}z + (1 - \sqrt{3}i)\)
(3) \(w = z^2\)
Kai
微分方程式
(1)
\[
(x^4 - 1)3ax^2 = a^2x^6 + 2x^3ax^3 - 3x^2 \Rightarrow a = 1 \Rightarrow y_p(x) = x^3
\]
(2)
\[
y = x^3 + \frac{1}{u}
\]
\[
(x^4 - 1)u' + 4x^3u = -1
\]
\[
(x^4 - 1) \neq 0 \text{ のとき, } u'+ \frac{4x^3}{x^4 - 1}u = \frac{1}{1 - x^4}
\]
\[
P(x) = \frac{4x^3}{x^4 - 1} \quad Q(x) = \frac{1}{1 - x^4}
\]
\[
u = e^{-\int P(x)\text{d}x}\big(\int Q(x)e^{\int P(x)\text{d}x}\text{d}x + C\big) = \frac{C - x}{x^4 - 1}
\]
\[
y = x^3 + \frac{x^4 - 1}{C - x}
\]
\[
(x^4 - 1) = 0\text{ のとき, 上式より }, y = x^3 =y_p,\text{ 微分方程式も満たす }
\]
\[
\therefore y = x^3 + \frac{x^4 - 1}{C - x}
\]
複素関数論
(1)
\[
w = z + (1 - \sqrt{3}i) = (1 + x) + (y - \sqrt{3})i
\]
\[
u = 1 + x \quad v = y - \sqrt{3}
\]
\[
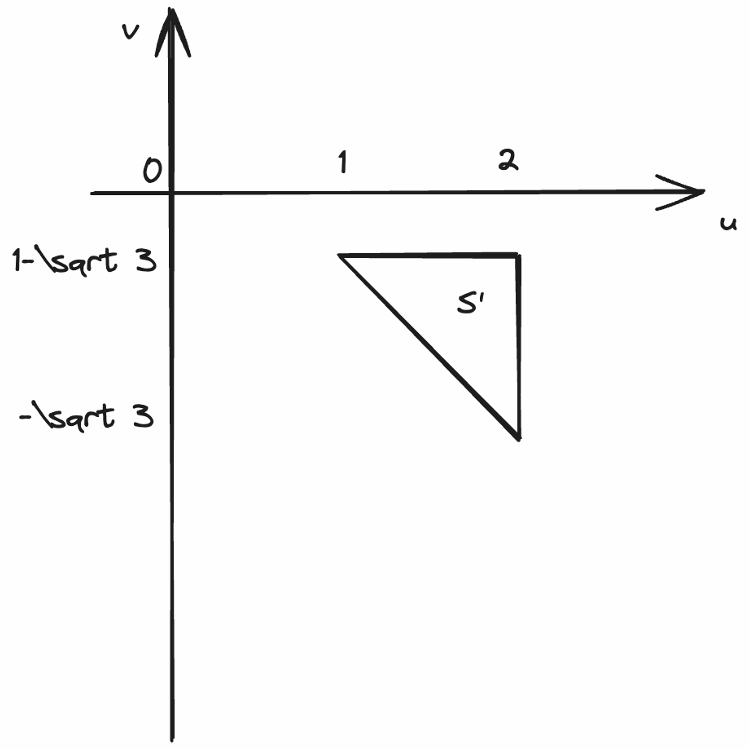
\begin{aligned}
x = 1,y = t(0 \le t \le 1) &\text{ とおくと, } u = 2,v = t - \sqrt{3} \\
u = 2(-\sqrt{3} &\le v \le 1 - \sqrt{3}) \\
x = t(0 \le t \le 1),y = 1 &\text{ とおくと, }u = 1 + t ,v = 1 - \sqrt{3} \\
v = 1 - \sqrt{3} &(1 \le u \le 2) \\
x = t(0 \le t \le 1),y = 1 - t &\text{ とおくと, }u = 1 + t.v = 1 - t - \sqrt{3} \\
v = -u + 2 - &\sqrt{3}(1 \le u \le 2)
\end{aligned}
\]
(2)
\[
w = 2e^{\frac{\pi i}{6}}z + (1 - \sqrt{3}i) = (\sqrt{3} + i)(x + iy) + (1 - \sqrt{3}i) = (\sqrt{3}x - y + 1) + (\sqrt{3}y + x -\sqrt{3})i
\]
\[
u = \sqrt{3}x - y + 1 \quad v = \sqrt{3}y + x - \sqrt{3}
\]
\[
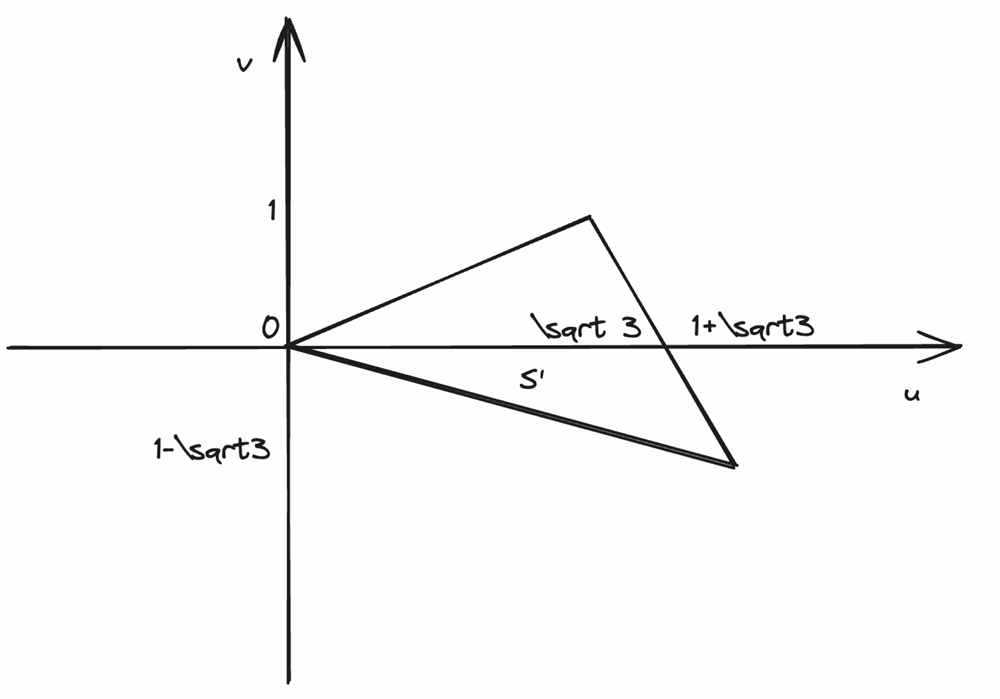
x = 1,y = t(0 \le t \le 1) \text{ とおくと, }u = \sqrt{3} + 1 - t,v = \sqrt{3}t + 1 - \sqrt{3}
\]
\[
v = 4 - \sqrt{3}u(\sqrt{3} \le u \le 1 + \sqrt{3})
\]
\[
x = t(0 \le t \le 1),y = 1 \text{ とおくと, } u = \sqrt{3}t,v = t
\]
\[
u = \sqrt{3}v(0 \le v \le 1)
\]
\[
x = t(0 \le t \le 1),y = 1 - t \text{ とおくと, } u = (1 + \sqrt{3})t,v = (1 - \sqrt{3})t
\]
\[
v = \frac{1 - \sqrt{3}}{1 + \sqrt{3}}u(0 \le u \le 1 + \sqrt{3})
\]
(3)
\[
w = z^2 = (x + iy)^2 = x^2 - y^2 - i \cdot 2xy
\]
\[
u = x^2 - y^2, \ v = 2xy
\]
\[
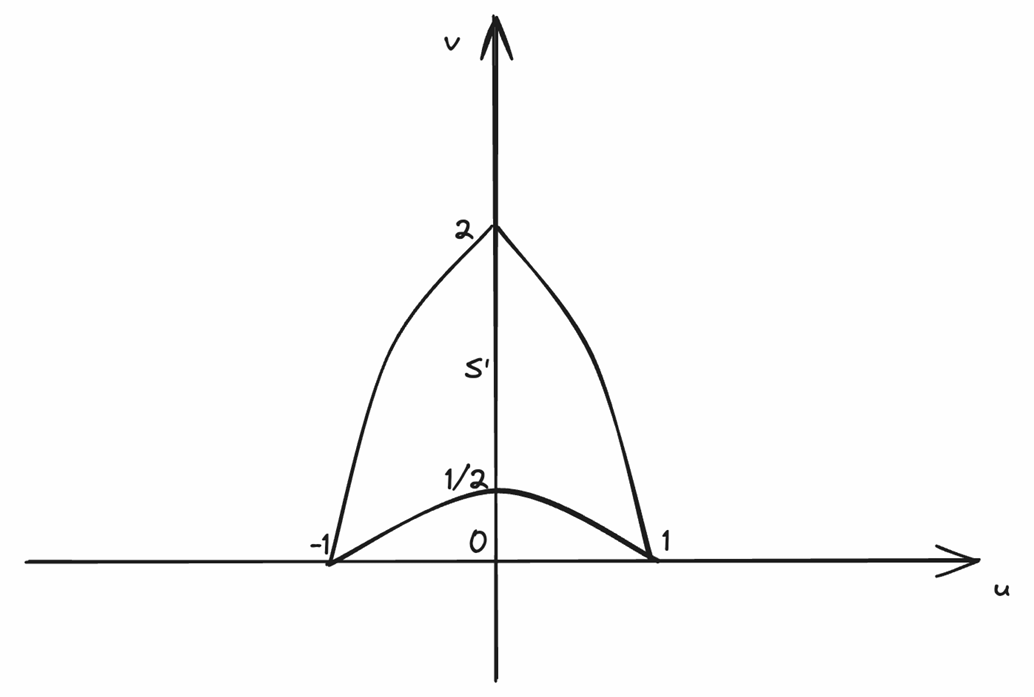
x = 1,y = t(0 \le t \le 1) \text{ とおくと, } u = 1 - t^2,v = 2t
\]
\[
u = 1 - \frac{v^2}{4}(0 \le v \le 2)
\]
\[
x = t(0 \le t \le 1),y = 1 \text{ とおくと, } u = t^2 - 1,v = 2t
\]
\[
u = \frac{v^2}{4} - 1(0 \le v \le 2)
\]
\[
x = t(0 \le t \le 1),y = 1 - t \text{ とおくと, } u = 2t - 1,v = 2t - 2t^2
\]
\[
v = \frac{1}{2} - \frac{u^2}{2}(-1 \le u \le 1)
\]