Kyushu-University
九州大学 システム情報科学府 情報理工学専攻・電気電子工学専攻 2016年度 複素関数論
Author Zero
Description 複素関数 \(f(z) = \frac{\pi\cot\pi z}{z^2 + a^2}\) を考える。ただし, \(a > 0\) とする。次の各問に答えよ。
(1) \(f(z)\) のすべての極における留数を求めよ。
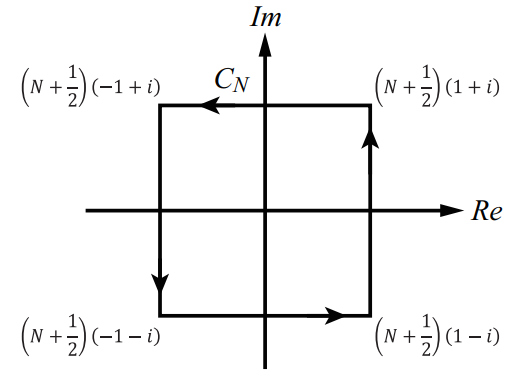
(2) 図に示す閉路 \(C_N\) に沿った複素積分 \(\oint_{C_N} f(z)dz\) を考える。ただし, \(N\) は自然数とする。\(\lim_{N \rightarrow \infty}\oint_{C_N}f(z)dz\) の値を求めよ。
(3) \(\lim_{N \rightarrow \infty}\oint_{C_N}f(z)dz\) の値を用して, \(\sum_{n=1}^{\infty}\frac{1}{n^2 + a^2} = \frac{\pi}{2a}\coth \pi a - \frac{1}{2a^2}\) を示せ。
Consider the complex function \(f(z) = \frac{\pi\cot\pi z}{z^2 + a^2}\) , where \(a > 0\) . Answer the following questions.
(1) Find the residues of \(f(z)\) at all its poles.
(2) Consider the complex integral \(\oint_{C_N} f(z)dz\) , where \(C_N\) is a closed path as shown in the figure and \(N\) is a natural number. Find the value of \(\lim_{N \rightarrow \infty}\oint_{C_N}f(z)dz\) .
(3) Using the value of \(\lim_{N \rightarrow \infty}\oint_{C_N}f(z)dz\) , prove that \(\sum_{n=1}^{\infty}\frac{1}{n^2 + a^2} = \frac{\pi}{2a}\coth \pi a - \frac{1}{2a^2}\) .
Kai (1)
\[
\begin{aligned}
f(z) &= \frac{\pi \cot \pi z}{z^2 + a^2} \\
&= \frac{\pi \cos \pi z}{(z^2 + a^2)\sin\pi z} \\
&= \frac{\pi \cos \pi z}{(z + ai)(z - ai)\sin \pi z}
\end{aligned}
\]
\(z = ai,-ai,n\) (\(n\) は整数)
\(\text{Res}_{z = ai}f(z)\) を求める。正則な関数 \(g(z) = \frac{\pi \cos \pi z}{(z + ai)\sin \pi z}\) とする。
\[
\begin{aligned}
\text{Res}_{z = ai}f(z) &= g(ai)\\
&= \frac{\pi \cos \pi(ai)}{2ai \cdot \sin\pi(ai)} \\
&= \frac{\pi \cdot \cosh(\pi a)}{2ai \cdot i\sinh(\pi a)} \\
&= -\frac{\pi}{2a} \coth(\pi a)
\end{aligned}
\]
次に、\(\text{Res}_{z = -ai}f(z)\) を求める。\(g(z) = \frac{\pi \cos\pi z}{(z - ai)\sin\pi z}\)
\[
\begin{aligned}
\text{Res}_{z = -ai}f(z) &= g(-ai)\\
&= \frac{\pi\cos\pi(-ai)}{(-2ai)\sin\pi(-ai)} \\
&= \frac{\pi\cosh(-\pi a)}{-2ai \cdot i \sinh(-\pi a)} \\
&= \frac{\pi}{2a}\coth(-\pi a) \\
&= -\frac{\pi}{2a}\coth \pi a
\end{aligned}
\]
最後に、\(\text{Res}_{z = n}f(z)\) を求める。
\[
\begin{aligned}
\text{Res}_{z = n}f(z) &= \lim_{z \rightarrow n} \pi \cdot \frac{1}{\{(z^2 + a^2) \tan \pi z\}'} \\
&= \lim_{z \rightarrow n} \pi \cdot \frac{1}{2z\tan \pi z + (z^2 + a^2) \cdot \frac{1}{\cos^2\pi z} \cdot \pi} \\
&= \lim_{z \rightarrow n} \pi \cdot \frac{\cos^2\pi z}{2z\sin\pi z \cos\pi z + \pi(z^2 + a^2)} \\
&= \lim_{z \rightarrow n} \pi \cdot \frac{\cos^2 \pi z}{z \sin 2\pi z + \pi(z^2 + a^2)} \\
&= \lim_{z \rightarrow n} \pi \cdot \frac{1}{\pi(n^2 + a^2)} \\
&= \frac{1}{n^2 + a^2}
\end{aligned}
\]
(2)
\[
\begin{aligned}
\oint_{C_N}f(x)dx &= \int_{-N}^N \frac{\pi \cot\pi(x - iN)}{(x - iN)^2 + a^2}dx \\
&\quad + \int_{N}^{-N} \frac{\pi\cot\pi(x + iN)}{(x + iN)^2 + a^2}dx \\
&\qquad + \int_{-N}^N \frac{\pi\cot\pi(N + iy)}{(N + iy)^2 + a^2}dy \\
&\qquad \quad + \int_{N}^{-N} \frac{\pi\cot\pi(-N + iy)}{(-N + iy)^2 + a^2}dy
\end{aligned}
\]
\[
\begin{aligned}
\bigg|\int_{-N}^N\frac{\pi \cot\pi(x - iN)}{(x - iN)^2 + a^2}dx\bigg| &= \bigg|\int_{N}^{-N} \frac{\pi\cot\pi(-N + iy)}{(-N + iy)^2 + a^2}dy\bigg| \\
\bigg|\int_{N}^{-N} \frac{\pi\cot\pi(x + iN)}{(x + iN)^2 + a^2}dx\bigg| &= \bigg|\int_{-N}^N \frac{\pi\cot\pi(N + iy)}{(N + iy)^2 + a^2}dy\bigg|
\end{aligned}
\]
より、
\[
\lim_{N \rightarrow \infty}\oint_{C_N}f(x)dx = 0
\]
(3)
留数定理から、
\[
\begin{aligned}
\lim_{N \rightarrow \infty}\oint_{C_N}f(z)dz &= 2\pi i \bigg(\sum_{n = -\infty}^{\infty} \frac{1}{n^2 + a^2} - \frac{\pi}{a}\coth \pi a\bigg) \\
0 &= 2\pi i \bigg(\sum_{n = -\infty}^{\infty}\frac{1}{n^2 + a^2} - \frac{\pi}{a}\coth\pi a\bigg) \\
\sum_{n = -\infty}^{\infty} \frac{1}{n^2 + a^2} &= \frac{\pi}{a}\coth \pi a \\
\sum_{n = -\infty}^{-1}\frac{1}{n^2 + a^2} + \frac{1}{a^2} + \sum_{n = 1}^{\infty}\frac{1}{n^2 + a^2} &= \frac{\pi}{a} \coth\pi a \\
2\sum_{n = 1}^{\infty}\frac{1}{n^2 + a^2} &= \frac{\pi}{a}\coth\pi a - \frac{1}{a^2} \\
\sum_{n = 1}^{\infty}\frac{1}{n^2 + a^2} &= \frac{\pi}{2a}\coth\pi a - \frac{1}{2a^2}
\end{aligned}
\]