九州大学 システム情報科学府 情報理工学専攻 2022年度 情報理論
Author
Description
【問 1】
\(k\) を正の整数とする。入力アルファベットが \(\mathcal{X} = \{0,1\}^k\) , 出力アルファベットふぁ \(\mathcal{Y} = \{0,1\}^k\) の無記憶な通信路 \(W(Y|X)\) を
\[
W(Y|X) =
\left\{
\begin{aligned}
&0 \quad (d(X,Y) = 0)\\
&\frac{1}{k} \quad (d(X,Y) = 1)\\
&0 \quad (d(X,Y) \ge 2)
\end{aligned}
\right.
\]
で定める。ただし, \(d(X,Y)\)は, \(X = (X_1,X_2,\cdots,X_k)\) と \(Y = (Y_1,Y_2,\cdots,Y_k)\) の問のハミング距離
\[
d(X,Y) = \sum_{i = 1}^k |X_i - Y_i|
\]
を表す。この通信路の通信路容量を求めよ。
【問 2】
アルファベットが \(\{1,2,3,4\}\) である単純マルコフ情報源の遷移確率行列が
\[
\begin{pmatrix}
0.5 & 0.5 & 0 & 0 \\
0 & 0.5 & 0 & 0.5 \\
0.5 & 0.5 & 0 & 0 \\
0 & 0 & \gamma & 1- \gamma \\
\end{pmatrix}
\]
で与えられたとする。ここで, \((i,j)\) 成分は遷移確率 \(P(j|i)\) を表し, \(0 < \gamma < 1\) とする。以下の問いに答えよ。
(1) このマルコフ情報源の状態遷移図を図示せよ。
(2) このマルコフ情報源の定常確率分布が \((1/8,1/4,1/8,1/2)\) であるとき, \(\gamma\) の値を求めよ。
(3) \(\gamma\) が前問で求めた値をとるとき, このマルコフ情報源のエントロピーレートを求めよ。
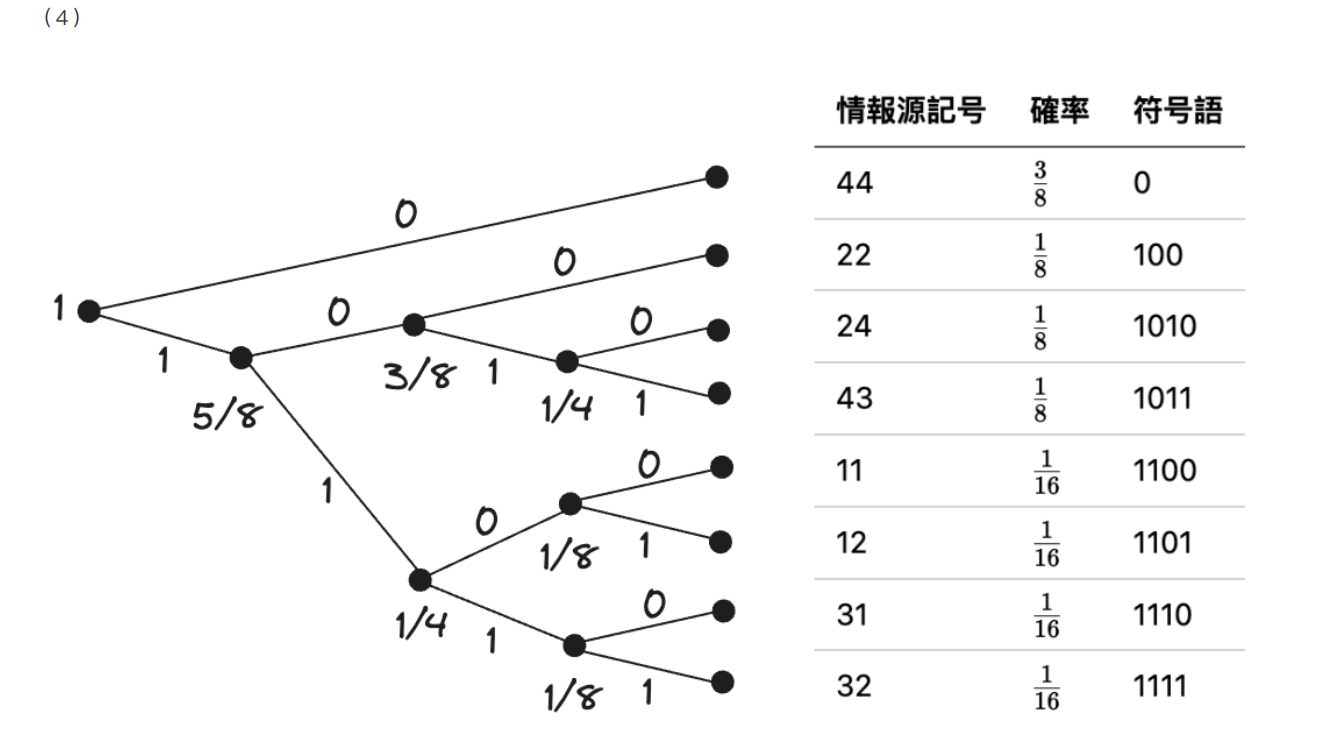
(4) このマルコフ情報源に従う確率変数の列 \(X_1,X_2,\dots\) を考える。 \(X_1\) が上記の定常確率分布 \((1/8,1/4,1/8,1/2)\) に従う場合, \((X_1,X_2)\) に対するハフマン符号化を行い, その符号の木を図示せよ。ただし, 符号語のアルファベットは \(\{0,1\}\) とする。
Kai
【問 1】
\[
C = \log_2s + \sum_{j = 1}^sp_{1j}\log_2p_{1j} = k + k \cdot \frac{1}{k}\log\frac{1}{k} = k - \log_2k
\]
【問 2】
(1)
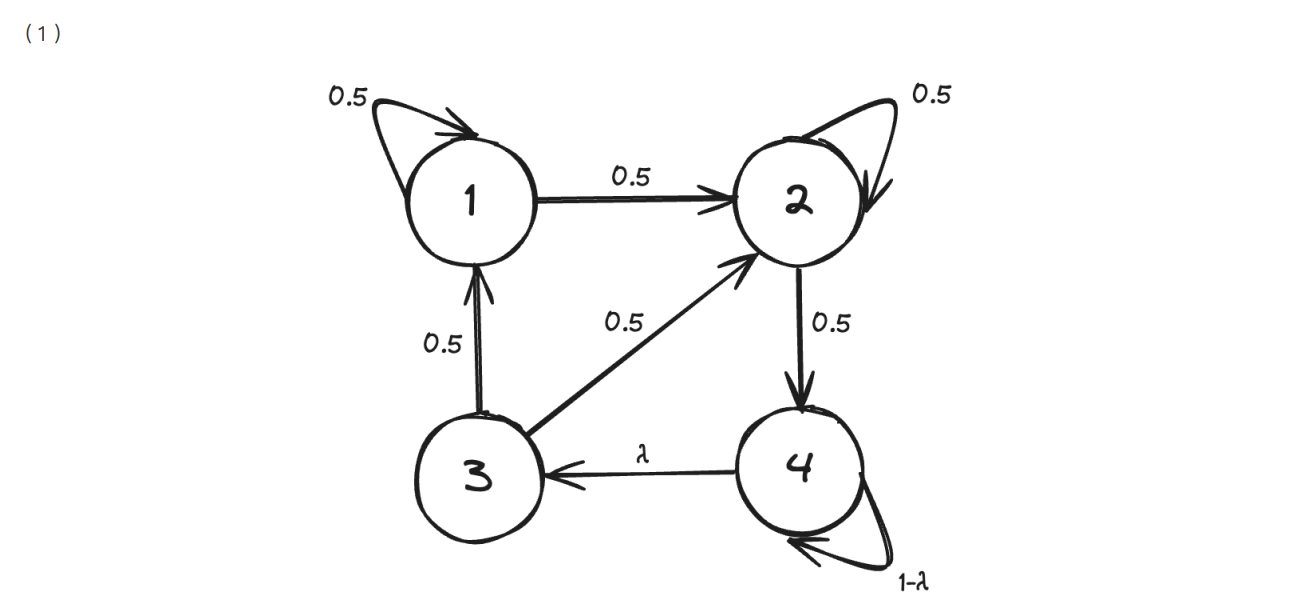
(2)
\[
w = (\frac{1}{8},\frac{1}{4},\frac{1}{8},\frac{1}{2})
\]
\[
\Pi =
\begin{bmatrix}
0.5 & 0.5 & 0 & 0 \\
0 & 0.5 & 0 & 0.5 \\
0.5 & 0.5 & 0 & 0 \\
0 & 0 & \gamma & 1- \gamma
\end{bmatrix}
\]
\[
w\Pi=w \Rightarrow \lambda = 0.25
\]
(3)
\[
\begin{aligned}
H(S_1) &= \mathcal{H}(0.5) = 1\\
H(S_2) &= \mathcal{H}(0.5) = 1\\
H(S_3) &= \mathcal{H}(0.5) = 1\\
H(S_4) &=\mathcal{H}(0.25) = 2 - \frac{3}{4}\log_2 3\\
H(S) &= \frac{1}{8}H(S_1) + \frac{1}{4}H(S_2) + \frac{1}{8}H(S_3) + \frac{1}{2}H(S_4) = \frac{3}{2} - \frac{3}{8}\log_2 3
\end{aligned}
\]
(4)