Skip to content

九州大学 システム情報科学府 情報理工学専攻 2021年度 アルゴリズム・プログラミング

Author

祭音Myyura

Description

【問 1】

2つの数の加算，乗算および大小比較は各々単位時間で行えるものとする．以下の各問いに答えよ．

(1) 与えられた \(d_1 \times d_2\) 行列 \(A\) と \(d_2 \times d_3\) 行列 \(B\) に対し，アルゴリズム 1 はそれらの積 \(C = AB\) を求める．アルゴリズム 1 の時間計算量を答えよ．

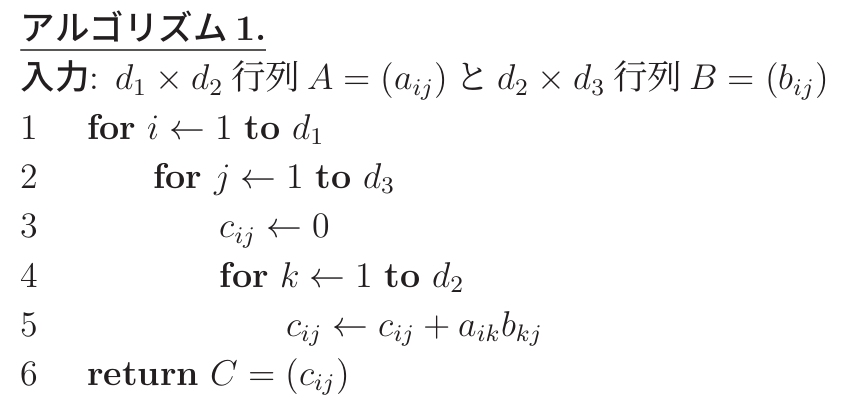
(2) \(10 \times 100\) 行列 \(A\) と \(100 \times 1\) 行列 \(B\) と \(1 \times 100\) 行列 \(C\) と \(100 \times 10\) 行列 \(D\) が与えられたとき，積 \(E = ABCD\) をアルゴリズム1をサブルーチンとして用いて求めたい．

  • (a) 数式 \(E = A(BC)D\) で表される積の順に従う場合，行列 \(E\) の計算における加算と乗算の回数の合計を答えよ．
  • (b) \(E\) の計算にかかる時間が最小となる積の順を，問 (a) に倣った数式で記述せよ．また，その積の順に従う \(E\) の計算における加算と乗算の回数の合計を答えよ．

(3) \(M_i, (i = 1, \ldots, n)\) は \(d_i \times d_{i+1}\) 行列とし，積 \(X = M_1 \cdots M_n\) をアルゴリズム 1 を用いて求めたい．積 \(X\) の計算について，すべての積の順の中で最小の時間計算量をアルゴリズム 2 が与えることを証明せよ．またアルゴリズム 2 の時間計算量を答えよ．

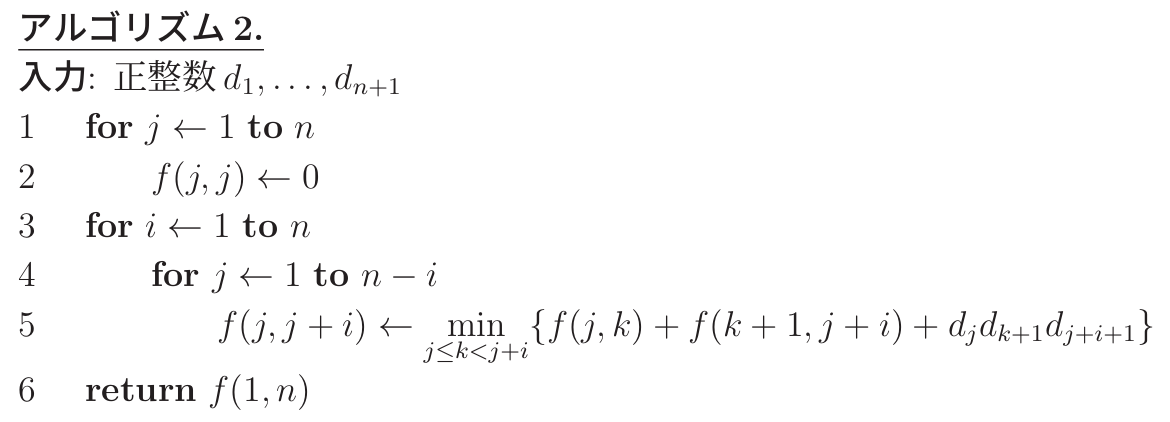
【問 2】

図 1 は Python 言語で書かれたマージソートのプログラムである．図 1 の 32 行目で下記の入力が与えられている．次の問いに答えよ．

32: list_input = [8, 3, 6, 5, 2, 7, 4, 1]

(1) merge_sort は，リスト result の要素を start から end の範囲で昇順に並び替える関数である．空欄(A)-(G)を埋め，関数merge sortを完成せよ．

(2) sort は，リスト list_input の要素を昇順に並び替える関数である．関数 sort が呼び出されて完了するまでに，関数 merge が呼び出される回数を答えよ．また，関数 merge に与えられる実引数のリスト copy と result の要素を関数 merge の呼び出しごとに答えよ．

(3) 8 行目から 11 行目の文を削除した場合を想定する．関数 sort が呼び出された時，リスト list_input の要素は，昇順に並び替えられているか否かを答えよ．また，関数 sort が実行完了するまでに，関数 merge_sort が呼び出される回数を答えよ．

(4) 関数 sort を，リスト list_input を降順に並び替えるように変更したい．行番号を示しながら，変更すべき式と，その内容を記せ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def sort(list_input):
    copy = list(list_input)
    merge_sort(copy, list_input, 0, len(list_input)-1)

def merge_sort(copy, result, start, end):
    if end - start < 1:
        return
    if end - start == 1:
        if result[start] > result[end]:
            result[start], result[end] = result[end], result[start]
        return

    mid = int((end + start) / 2)
    merge_sort(result, copy, (A), (B))
    merge_sort(result, copy, (C), (D))
    merge(copy, result, (E), (F), (G))

def merge(copy, result, start, end, mid):
    i = start
    j = mid
    idx = start

    while idx <= end:
        if j > end or (i < mid and copy[i] < copy[j]):
            result[idx] = copy[i]
            i += 1
        else:
            result[idx] = copy[j]
            j += 1
        idx += 1

list_input=[8, 3, 6, 5, 2, 7, 4, 1]
sort(list_input)
print(list_input)

図1 (Figure 1)

Kai

【問 1】

(1)

\(O(d_1 \cdot d_2 \cdot d_3)\)

(2)

(a)

\((100000 + 10000 + 1000) \times 2 = 240000\)

(b)

\((1000 + 1000 + 100) \times 2 = 4200\)

\(E = (AB)(CD)\)

(3)

Statement A: Suppose that an optimal parenthesization (order of multipications) of \(M_i M_{i+1} \cdots M_j, (1 \le i < j \le n)\) splits the product between \(M_k\) and \(M_{k+1}\). Then the parenthesization of the "left" subchain \(M_i M_{i+1} \cdots M_k\) within this optimal parenthesization of \(M_i M_{i+1} \cdots M_j\) is also an optimal parenthesization of \(M_i M_{i+1} \cdots M_k\).

Statement A can be proved by contradicition. Assume that there exits a less costly way to parenthesize \(M_i M_{i+1} \cdots M_k\), then, substituting that parenthesization in the optimal parenthesization of \(M_i M_{i+1} \cdots M_j\) would produce another parenthesization of \(M_i M_{i+1} \cdots M_j\) of a lower cost than the optimum, which is a contradiction.

Similar for the "right" subchain, it is also an optimal parenthesization of \(A_{k+1} A_{k+2} \cdots A_j\).

Therefore, let \(f(i, j)\) be the minimum number of multiplications needed to compute the matrix \(A_{i\ldots j} = A_i A_{i+1} \cdots A_{j}\). By statement A, we assume that an optimal parenthesization splits the product \(A_i A_{i+1} \cdots A_{j}\) between \(A_k\) and \(A_{k+1}\). Then, \(f(i, j)\) is equal to the minimum cost for computing the subproducts \(A_{i\ldots k}\) and \(A_{k+1\ldots j}\) plus the cost of multiplying these two matrices, i.e.,

\[ f(i, j) = f(i, k) + f(k+1, j) + d_{i} d_{k+1} d_{j+1} \]

Since there are only \(j - i\) possible values for \(k\), namely \(k = i, i+1, \ldots, j-1\). Hence we have

\[ f(i, j) = \left\{ \begin{aligned} &0 &\text{if } i=j, \\ &\min_{i \le k < j} f(i, k) + f(k+1, j) + d_{i} d_{k+1} d_{j+1} &\text{if } i < j. \end{aligned} \right. \]

Thus the correctness of algorithm 2 is proved.

The time complexity of algorithm 2 is \(O(n^3)\).

【問 2】

(1)

  • (A): start
  • (B): mid - 1
  • (C): mid
  • (D): end
  • (E): start
  • (F): end
  • (G): mid

(2)

4 time

1
2
3
4
5
6
7
1: copy [8, 3, 6, 5, 2, 7, 4, 1], result [8, 3, 6, 5, 2, 7, 4, 1]

2: copy [3, 6, 8, 5, 2, 7, 1, 4], result [8, 3, 6, 2, 5, 7, 4, 1]

3: copy [8, 3, 6, 2, 5, 1, 4, 7], result [3, 6, 8, 5, 2, 7, 1, 4]

4: copy [3, 6, 8, 1, 2, 4, 5, 7], result [8, 3, 6, 2, 5, 1, 4, 7]

(3)

(Confused, since the program may never stop running when start=1 and end=2.)

(4)

  • line 9: if result[start] < result[end]:
  • line 24: if j > end or (i < mid and copy[i] > copy[j]):