九州大学 システム情報科学府 情報理工学専攻 2020年度 情報理論
Author
Yu
Description
【問 1】
下図は, 定常 \(2\) 重マルコフ情報源 \(S\) の状態遷移図である. 下記の設問に答えよ.
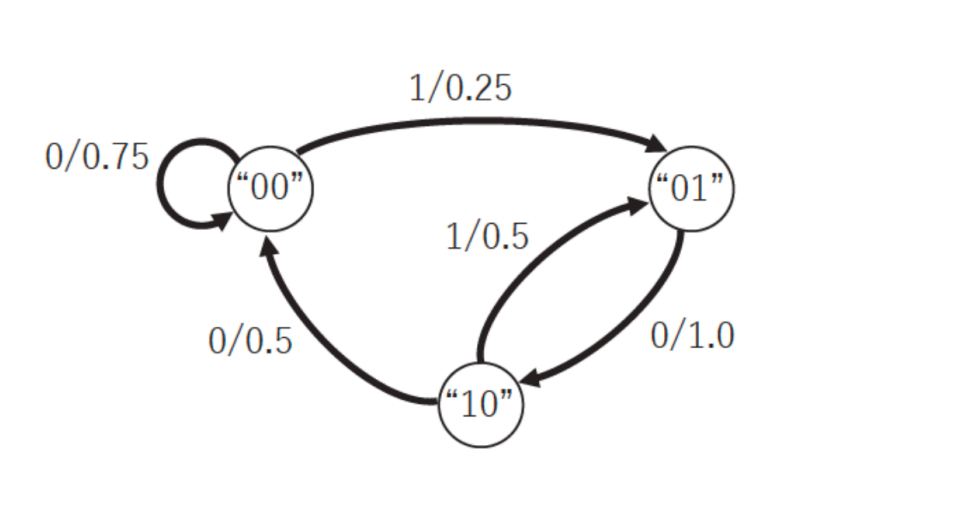
(1) 上図の状態遷移図を元に, このマルコフ情報源 \(S\) の遷移確率行列 \(A\) を求めよ. ただし, 状態 "\(00\)","\(10\)", "\(01\)" の順に, 行を記せ.
(2) 時点 \(0\) で状態 "00" にいたとして, 時点 \(2\) で状態 "10" にいる確率はいくらか答えよ.
(3) 上記のマルコフ情報源 \(S\) の定常分布 \(\vec{w} = (w_1,w_2,w_3)\) を求めよ. ただし, \(w_i\) の添え字 \(i = 1,2,3\) は状態 "\(00\)", "\(10\)", "\(01\)" にそれぞれ対応するものとする.
(4) 定常 \(2\) 重マルコフ情報源 \(X_1,X_2,\dots\) のエントロピーレート \(\lim_{n \rightarrow \infty} \frac{1}{n}H(X_1,X_2,\dots,X_n)\) が \(H(X_3|X_1,X_2)\) に一致することを示せ. ただし, \(H(X_3|X_1,X_2)\) は条件付きエントロピーである.
(5) 上記のマルコフ情報源 \(S\) に対するエントロピーレート \(H(S)\) を求めよ.
【問 2】
\(X,Y\) を \(\{0,1\}\) に値をとる確率変数とする. パラメータ \(\alpha,\beta,\gamma \in [0,1]\) に対し,
\[
\begin{aligned}
P(X = 0) = \alpha &,\quad P(X = 1) = 1 - \alpha,\\
P(Y = 0|X = 0) = \beta &,\quad P(Y = 1|X = 0) = 1 - \beta,\\
P(Y = 0|X = 1) = \gamma &,\quad P(Y = 1|X = 1) = 1 - \gamma,
\end{aligned}
\]
とする. \(2\) 値エントロピー関数を
\[
h(p) =
\left \{
\begin{aligned}
-p\log p - (1 - p)\log(1 - p) , \quad &\text{for} \quad 0 < p < 1, \\
0,\qquad \qquad \qquad \qquad \qquad \qquad &\text{for} \quad p = 0,1
\end{aligned}
\right.
\]
とする. 以下の問いに答えよ.
(1) 条件付きエントロピー \(H(Y|X)\) を \(2\) 値エントロピー関数を用いて表現せよ.
(2) \(\beta = 1 - \gamma\) とする. このとき, 相互情報量 \(I(X;Y)\)を最大化する\(\alpha\) を求めよ. また \(I(X;Y)\) の最大値を \(2\) 値エントロピー関数と \(\alpha,\beta\) を用いて表現せよ.
(3) \(\alpha,\beta\) をある値に固定する. ただし, \(0 < \alpha < 1\) とする. 相互情報量 \(I(X;Y)\) を最小化する \(\gamma\) の値を \(\alpha,\beta\) を用いて表せ. また, その最小値を示せ.
(4) \(\alpha,\beta\) をある値に固定する. ただし, \(0 < \alpha < 1 ,\beta > \frac{1}{2}\) とする. 相互情報量 \(I(X;Y)\) を最大化する \(\gamma\) の値を求めよ.
Kai
【問 1】
(1)
\[
\begin{bmatrix}
\frac{3}{4} & 0 & \frac{1}{4} \\
\frac{1}{2} & 0 & \frac{1}{2} \\
0 & 1 & 0
\end{bmatrix}
\]
(2)
\[
A^2 =
\begin{bmatrix}
\frac{9}{16} & \frac{1}{4} & \frac{3}{16} \\
\frac{3}{8} & \frac{1}{2} & \frac{1}{8} \\
\frac{1}{2} & 0 & \frac{1}{2}
\end{bmatrix}
\Rightarrow P = \frac{1}{4}
\]
(3)
\[
\left\{
\begin{aligned}
&w_1 + w_2 + w_3 = 1 \\
&\vec{w}A = \vec{w}
\end{aligned}
\right. \Rightarrow \vec{w} = (\frac{1}{2},\frac{1}{4},\frac{1}{4})
\]
(4)
\[
\begin{aligned}
\lim_{n \rightarrow \infty} \frac{1}{n}H(X
_1,X_2,\dots,X_n) &= \lim_{n \rightarrow \infty} \frac{1}{n}[H(X_1) + H(X_2|X_1) + H(X_3|X_1,X_2) + \cdots + H(X_n|X_1,\dots,X_{n-1})] \\
&= \lim_{n \rightarrow \infty} \frac{1}{n}[H(X_1) + H(X_2|X_1) + H(X_3|X_1,X_2) + \cdots + H(X_n|X_{n-2},X_{n-1})] \\
&= \lim_{n \rightarrow \infty}\frac{1}{n}[H(X_3|X_1,X_2) + \cdots + H(X_n|X_{n-2},X_{n-1})] \\
&= \lim_{n \rightarrow \infty}\frac{n-2}{n}H(X_3|X_1,X_2)\\
&= H(X_3|X_1,X_2)
\end{aligned}
\]
(5)
\[
H(S) = w_1\mathcal{H}(\frac{1}{4}) + w_2\mathcal{H}(\frac{1}{2}) + w_3\mathcal{H}(1) = \frac{5}{4} - \frac{3}{8}\log_2 3
\]
【問 2】
(1)
\[
H(Y|X) = \alpha h(\beta) + (1 - \alpha)h(\gamma)
\]
(2)
\[
\alpha = \frac{1}{2}
\]
\[
\max_{\alpha}I(X;Y) = 1 - h(\beta)
\]
(3)
\[
\gamma = \beta
\]
\[
\min_{\gamma}I(X;Y) = 0
\]
(4)
\[
\begin{aligned}
I(X;Y) &= H(Y) - H(Y|X) = h(\alpha\beta + (1 - \alpha)\gamma) - \alpha h(\beta) - (1 - \alpha)h(\gamma) \\
f(\gamma) &= h(\alpha\beta + (1 - \alpha)\gamma) - (1 - \alpha)h(\gamma)\text{の最大値問題を解くことになる}
\end{aligned}
\]
\[
\gamma = 0
\]
