九州大学 システム情報科学府 情報理工学専攻 2020年度 オートマトンと言語

Author

Casablanca

Description

【問１】

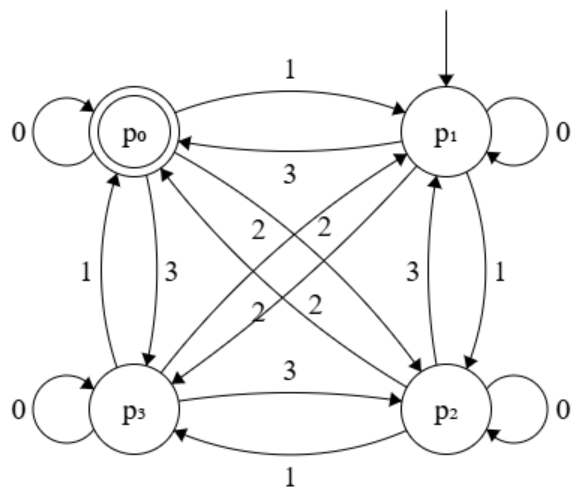
決定性有限オートマトン \(M_1 = (P, \Sigma, \delta_1, p_1, F_1)\) を考える． ただし，\(P\), \(\Sigma\), \(\delta_1\), \(p_1\), \(F_1\) はそれぞれ \(M_1\) の状態集合，アルファベット，遷移関数，初期状態，最終状態の集合を表す． \(P = \{p_0, p_1, p_2, p_3\}\), \(\Sigma = \{0, 1, 2, 3\}\), \(F_1 = \{p_0\}\) であり，\(i = 1,2,3,4\) に対し \(\delta_1 (p_i, a) = p_{(i + n(a)) \text{ mod } 4}\) である． ここで \(n(a)\) は記号 \(a \in \Sigma\) に対応する整数であり，\(n(0) = 0\), \(n(1) = 1\), \(n(2) = 2\), \(n(3) = 3\) である． 非負の整数 \(x\) と正の整数 \(y\) に対し，\(x \text{ mod } y\) は \(x\) を \(y\) で割ったときの余りを表す． たとえば \(\delta_1(p_1, 3) = p_0\) となる．次の各問いに答えよ．

(1) \(M_1\) の状態遷移図を与えよ．

(2) 決定性有限オートマトン \(M_2 = (P, \Sigma, \delta_1, p_1, F_2)\) は，\(M_1\) と同じ状態集合，アルファベット，遷移関数，初期状態を持つ． \(M_2\) と等価な決定性有限オートマトンの最小状態数が \(2\) であるとき，最終状態の集合 \(F_2 \subseteq P\) の例をひとつ与えよ．

(3) \(\Sigma\) 上の文字列 \(u\) に対して，

\[ Y(u) = \begin{cases} &1 &\text{if } u \text{ is the empty string}, \\ &Y(v) \times n(a) &\text{if } u = va, v \in \Sigma^*, a \in \Sigma. \end{cases} \]

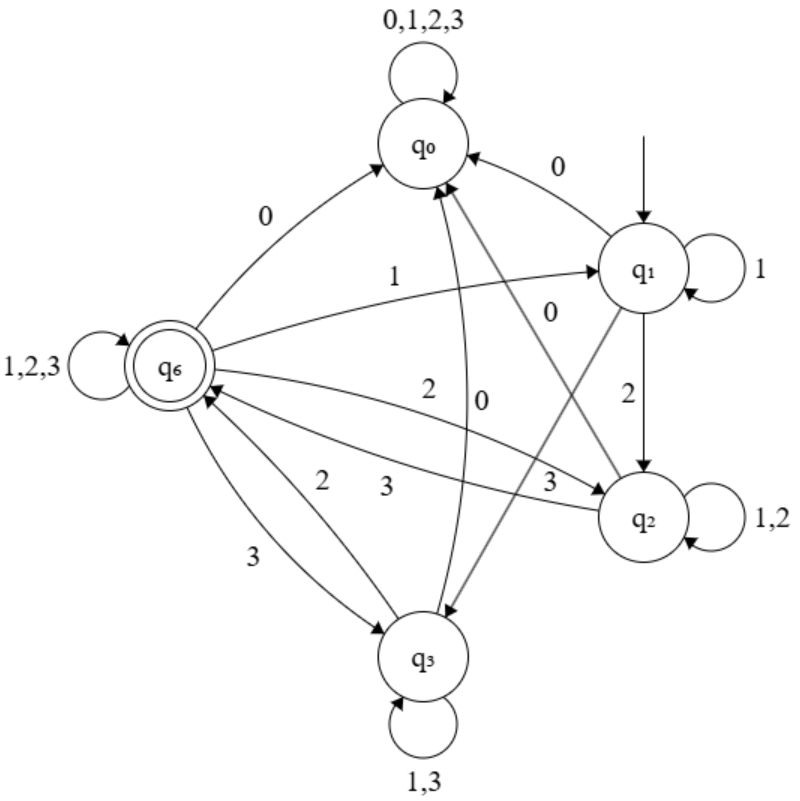
とする．\(Y(u) \text{ mod } 6 = 0\) かつ \(Y(u) \neq 0\) となる \(u\) のみを受理する決定性有限オートマトン \(M_3\) を考える． ただし，\(M_3\) の状態集合を \(\{q_0, q_1, q_2, q_3, q_6\}\), 初期状態を \(q_1\), 最終状態の集合を \(\{q_6\}\) とする． また，各状態は次のような文字列に対応する．

• \(q_0\) は \(Y(u) = 0\) を満たす文字列 \(u\) に対応．
• \(q_1\) は \(Y(u) \text{ mod } 2 \neq 0\) かつ \(Y(u) \text{ mod } 3 \neq 0\) を満たす文字列 \(u\) に対応．
• \(q_2\) は \(Y(u) \text{ mod } 2 = 0\) かつ \(Y(u) \text{ mod } 6 \neq 0\) を満たす文字列 \(u\) に対応．
• \(q_3\) は \(Y(u) \text{ mod } 3 = 0\) かつ \(Y(u) \text{ mod } 6 \neq 0\) を満たす文字列 \(u\) に対応．
• \(q_6\) は \(Y(u) \text{ mod } 6 = 0\) かつ \(Y(u) \neq 0\) を満たす文字列 \(u\) に対応．

\(M_3\) の状態遷移図を与えよ．

【問２】

アルファベット \(\Sigma = \{a, b\}\) 上の文字列 \(w\) に対し，\(w\) の長さを \(|w|\) と表す． また，\(1 \leq i \leq |w|\) に対して \(w[i]\) は \(w\) の \(i\) 番目の文字を表す． \(w\) の逆文字列を \(w^R\) と表す． \(|x| = |y| \geq 1\) を満たす \(\Sigma\) 上の文字列 \(x\) と \(y\) に対して，\(d(x,y) = |\{ i \mid 1 \leq i \leq |x|, x[i] \neq y[i]\}|\) とする． 文字列 \(w\) に対し，\(w = xyz\) を満たす文字列 \(x, z \in \Sigma^*\) が存在するとき，\(y\) を \(w\) の部分文字列という． \(\#\) は \(\Sigma\) に含まれない文字とする． 次の各言語を考える．

\[ \begin{aligned} L_0 &= \{w \mid w \in \Sigma^*, w = w^R\} \\ L_1 &= \{wxw^R \mid w \in \Sigma^*, x \in \Sigma\} \\ L_2 &= \{uxvw \mid u, v, w \in \Sigma^*, uv = w^R, x \in \Sigma\} \\ L_3 &= \{uv \mid u, v \in \Sigma^*, |u| = |v| \geq 1, d(u^R, v) \leq 1\} \\ L_4 &= \{x \# w \mid x, w \in \Sigma^*, x^R \text{ is a substring of } w\} \end{aligned} \]

これらの言語はすべて文脈自由言語である．例えば，言語 \(L_0\) は以下の生成規則を持つ文脈自由文法によって生成される．

\[ S \to aSa \mid bSb \mid a \mid b \mid \varepsilon \]

ただし，\(\varepsilon\) は空文字列を表す．

次の問いに答えよ．

(1) 言語 \(L_1\) を生成する文脈自由文法の生成規則を与えよ．ただし，非終端記号を \(S\) とし，開始記号を \(S\) とする．

(2) 言語 \(L_2\) を生成する文脈自由文法の生成規則を与えよ．ただし，非終端記号を \(S, T\) とし，開始記号を \(S\) とする．

(3) 言語 \(L_3\) を生成する文脈自由文法の生成規則を与えよ．ただし，非終端記号を \(S, T\) とし，開始記号を \(S\) とする．

(4) 言語 \(L_4\) を生成する文脈自由文法の生成規則を与えよ．ただし，非終端記号を \(S, T, X\) とし，開始記号を \(S\) とする．

Kai

【問１】

(1)

(2)

\[ F_2 = \{p_0, p_2\} \]

(3)

\[ Y(u) \text{ mod } 6 \equiv 0, Y(u) \neq 0 \]

【問２】

(1)

\[ S \to aSa \mid bSb \mid a \mid b \]

(2)

\[ \begin{aligned} S &\to aSa \mid bSb \mid aT \mid bT \\ T &\to aTa \mid bTb \mid \varepsilon \end{aligned} \]

(3)

\[ \begin{aligned} S &\to aSa \mid bSb \mid \varepsilon \mid aTb \mid bTa \\ T &\to aTa \mid bTb \mid \varepsilon \end{aligned} \]

(4)

\[ \begin{aligned} S &\to TX \\ T &\to aTa \mid bTb \mid \# X \\ X &\to aX \mid bX \mid \varepsilon \end{aligned} \]