九州大学 システム情報科学府 情報理工学専攻 2019年度 情報理論
Author
Yu
Description
【問 1】
情報源アルファベットが \(\mathcal{X}=\{a,b,c,d\}\) の離散無記憶情報源があり, 記号 \(x \in \mathcal{X}\) の出現確率 \(p(x)\) が以下の表で与えられている。ただし, \(0 <\alpha \le \frac{1}{2}\) とする。
| \(x\) |
\(a\) |
\(b\) |
\(c\) |
\(d\) |
| \(p(x)\) |
\(\frac{\alpha}{2}\) |
\(\frac{1-\alpha}{2}\) |
\(\frac{1}{4}\) |
\(\frac{1}{4}\) |
以下の問いに答えよ。
(1) この情報源のエントロピーを \(\alpha\) の関数として求めよ。
(2) \(0 < \alpha < \frac{1}{4}\) のときのこの情報源に対する \(2\) 元ハフマン符号を \(1\) つ求めよ。
(3) (2)の符号の平均符号長 (符号長の期待値)を \(\alpha\) の関数として求めよ。
(4) \(\frac{1}{4} \le \alpha \le \frac{1}{2}\) のときのこの情報源に対する \(2\) 元ハフマン符号の平均符号長を求めよ。
(5) この情報源に対する \(2\) 元ハフマン符号の平均符号長を \(L(\alpha)\) とおく。 \(\alpha \in (0,\frac{1}{2}]\) に対する \(L(\alpha)\) のガラフをかけ。
【問 2】
アルファベット \(\{1,2,3\}\) 上の \(\text{Markov}\) 情報源 \(X_1X_2\cdots\) の遷移確率行列が
\[
P = (p_{ij}) =
\begin{pmatrix}
0.25 & 0.25 & 0.5 \\
0.4 & 0.6 & 0 \\
0 & 0.2 & 0.8
\end{pmatrix}
\]
で与えられているとき, 次の各問に答えよ。ただし, \(p_{ij}\) は \(X_t = i\) のもとで \(X_{t + 1} = j\) となる条件付き確率を表す。
(1) \(P\) の固有値の一つが \(1\) であることを示せ。
(2) 行ベクトル \(v\) が固有値 \(1\) に対応する \(P\) の左固有ベクトルであり, その要素の総和が \(1\) であるとする。\(v\) の持つ意味を述べよ。ただし, 固有値 \(\lambda\) に対応する \(P\) の左固有ベクトルとは, \(vP = \lambda v\) を満たすゼロでない行ベクトル \(v\) のことである。
(3) 固有値 \(1\) に対応する \(P\) の右固有ベクトルを求めよ。ただし, 固有値 \(\lambda\) に対応する \(P\) の右固有ベクトルとは, \(Pu = \lambda u\) を満たすゼロでない列ベクトル \(u\) のことである。
(4) 任意のベクトル \(v\) について, \(||v||_1\) でその要素の絶対値の総和を表す。行ベクトル \(v\) について, \(||vP||_1 \le ||v||_1\) を示せ。
(5) \(P\) の任意の固有値の絶対値は \(1\) 以下であることを示せ。
Kai
【問 1】
(1)
\[
H(S) = 1 - \frac{\alpha}{2}\log_2\frac{\alpha}{2} - \frac{1 - \alpha}{2} \log_2\frac{1-\alpha}{2}
\]
(2)
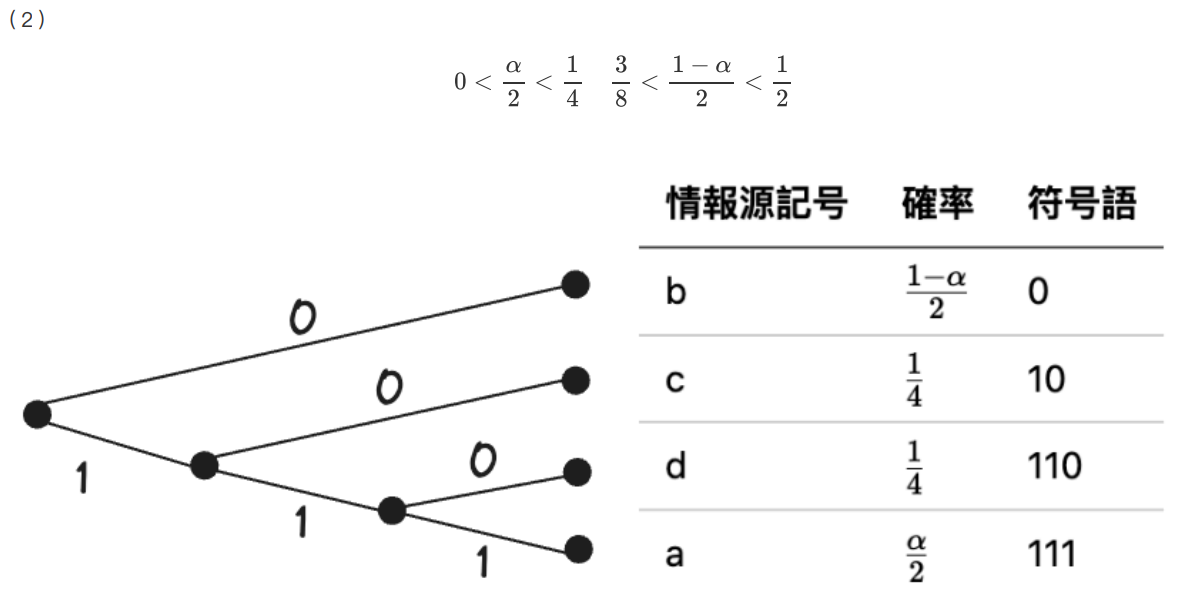
(3)
\[
\bar{L} = \frac{1 - \alpha}{2} + \frac{1}{4} \cdot 2 + (\frac{1}{4} + \frac{\alpha}{2}) \cdot 3 = \frac{7}{4} - \frac{\alpha}{3} (\text{ビット})
\]
(4)
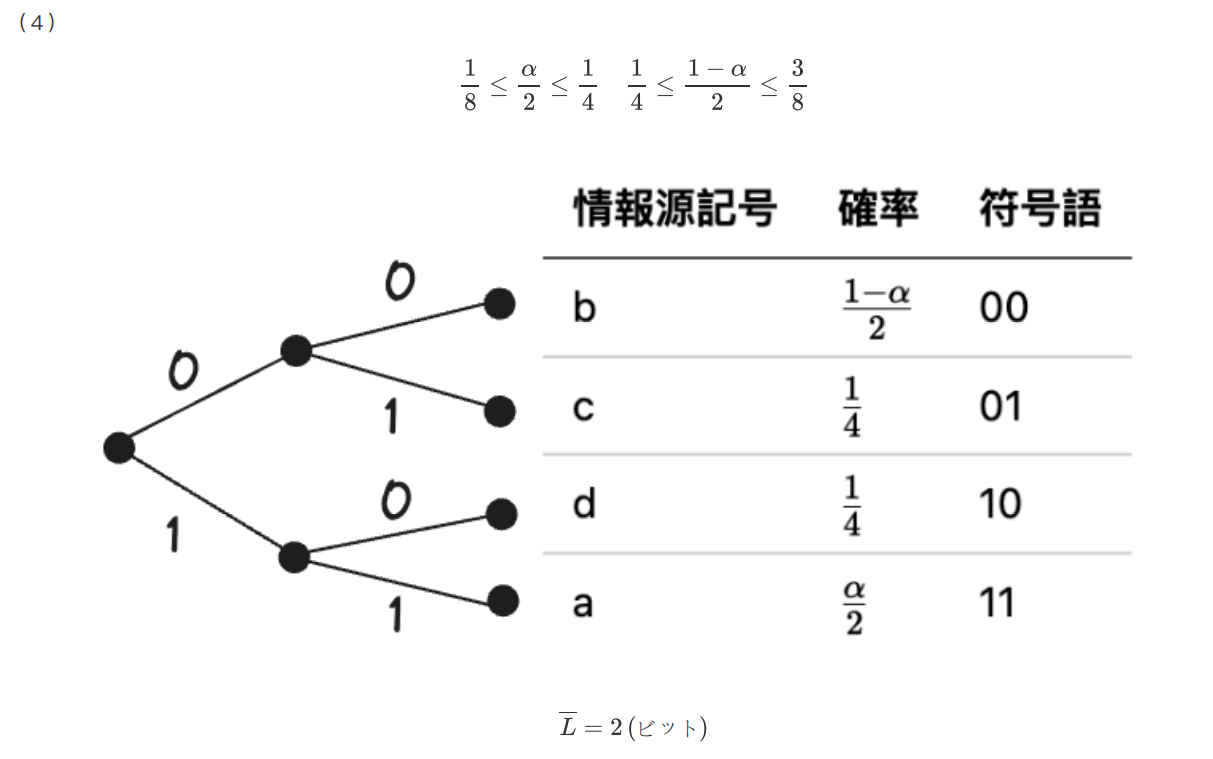
(5)
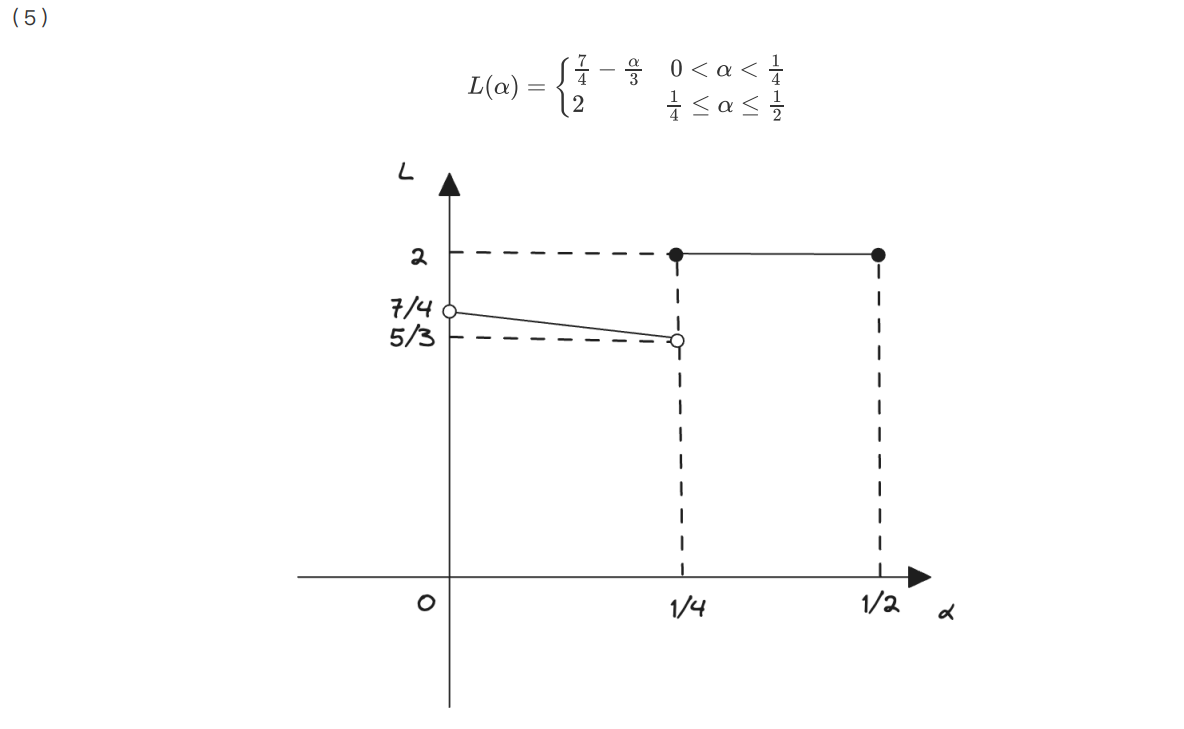
【問 2】
(1)
\[
|T| = |\lambda E - P| =
\begin{vmatrix}
\lambda - 0.25 & -0.25 & -0.5\\
-0.4 & \lambda - 0.6 & 0 \\
0 & -0.2 & \lambda - 0.8
\end{vmatrix}
\]
\[
\lambda = 1 \text{とすると, } |T| =
\begin{vmatrix}
0.75 & -0.25 & -0.5 \\
-0.4 & 0.4 & 0 \\
0 & -0.2 & 0.2
\end{vmatrix} = 0
\]
(2)
\(v\) はマルコフ情報源の定常分布
(3)
\[
Tu = 0 \Rightarrow u =
\begin{bmatrix}
1 \\
1 \\
1 \\
\end{bmatrix}
\]
(4)
\[
\begin{aligned}
||vP||_1 &= |v_1p_{11} + v_2p_{21} + v_3p_{31}| + |v_1p_{12} + v_2p_{22} + v_3p_{32}| + |v_1p_{13} + v_2p_{23} + v_3p_{33}| \\
&\le (|v_1p_{11}| + |v_2p_{21}| + |v_3p_{31}|) + (|v_1p_{12}| + |v_2p_{22}| + |v_3p_{32}|) + (|v_1p_{13}| + |v_2p_{23}| + |v_3p_{33}|) \\
&= |v_1|\sum_{j = 1}^3p_{1j} + |v_2|\sum_{j = 1}^3p_{2j} +|v_3|\sum_{j = 1}^3p_{3j} \\
&= |v_1| + |v_2| + |v_3| \\
&= ||v||_1
\end{aligned}
\]
(5)
\[
\begin{aligned}
||Pv||_1 &= |p_{11}v_1 + p_{12}v_1 + p_{13}v_1| + |p_{21}v_2 + p_{22}v_2 + p_{23}v_2| + |p_{31}v_3 + p_{32}v_3 + p_{33}v_3| \\
&\le (|p_{11}v_1 | + |p_{12}v_1| + |p_{13}v_1|) + (|p_{21}v_2| + |p_{22}v_2| + |p_{23}v_2|) + (|p_{31}v_3| + |p_{32}v_3| + |p_{33}v_3|) \\
&= |v_1|\sum_{j = 1}^3 p_{1j} + |v_2|\sum_{j = 1}^3 p_{2j} + |v_3|\sum_{j = 1}^3 p_{3j} \\
&= |v_1| + |v_2| + |v_3| \\
&= ||v||_1 \\
Pv &= \lambda v \text{とすると,}||Pv||_1 = ||\lambda v||_1 = |\lambda v_1| + |\lambda v_2| + |\lambda v_3| = |\lambda| \cdot ||v||_1 \\
||Pv||_1 &\le ||v||_1 \Rightarrow |\lambda| \cdot ||v||_1 \le ||v||_1 \Rightarrow |\lambda| \le 1
\end{aligned}
\]


