九州大学 システム情報科学府 情報理工学専攻 2019年度 オートマトンと言語
Author
Zero
Description
【問1】
以下の状態遷移図を持つ非決定性有限オートマトン \(M = (K, \Sigma, \delta, q_0, F)\) に対し、次の各問いに答えよ。 ただし、\(K = \{ q_0, q_1 \}\), \(\Sigma = \{ a, b \}\), \(\delta\), \(q_0\), \(F = \{ q_0, q_1 \}\) は、それぞれ状態の集合、アルファベット、遷移関数、初期状態、最終状態の集合を表す。
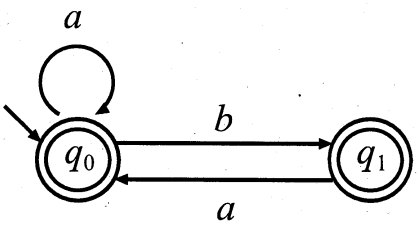
(1) \(M\) が受理する長さ 4 の文字列をすべて列挙せよ。
(2) \(M\) が受理する言語 \(L_1\) に含まれる文字列を説明せよ。
(3) \(L_1\) を受理する状態数最小の決定性有限オートマトンの状態遷移図を与えよ。
(4) 文字 \(a\) で始まり文字 \(b\) で終わる \(\Sigma\) 上の文字列の集合を言語 \(L_2\) とする。 言語 \(L_1 \cap L_2\) を受理する状態数最小の決定性有限オートマトンの状態遷移図を与えよ。
【問2】
1+2+3 や 4+4−10 のように数の加減算を行う式を扱える、次の文脈自由文法 \(G\) を考える。 文法 \(G\) の終端記号は \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, −\)、非終端記号は \(S, N, D\)、開始記号は \(S\) であり、生成規則は次の通りである。
開始記号 \(S\) から生成規則に従った書換えにより導出できる文字列が、\(G\) によって生成される文字列である。 例えば \(G\) は文字列 4+4−10 を次の導出木により生成する。
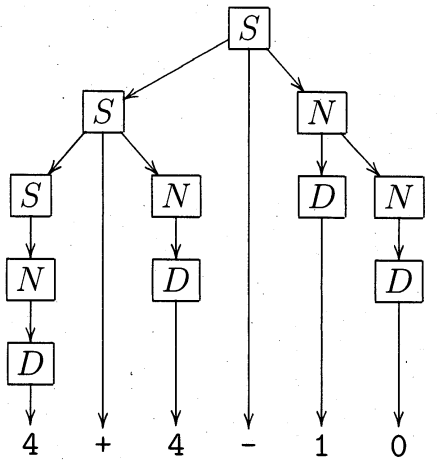
次の各問い (1), (2) に答えよ。
(1) 次の各文字列は \(G\) によって生成されるか。されるならば導出木を与え、されないならば理由を説明せよ。
- (a) 5+13+9
- (b) 25
- (\(c\)) 空文字列
- (d) -4+15
(2) \(G\) は 05+3-0007 のように個々の数を表す部分の先頭に不要な 0 が付いた文字列も生成してしまう。 このような文字列が生成されないように修正した文法 \(G'\) を考える。 文法 \(G'\) の終端記号は \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, −\)、非終端記号は \(S, N, M, D\)、開始記号は \(S\) であり、生成規則は次の通りである。 ただし \(\varepsilon\) は空文字を表す。
\(G'\) が意図通りになるよう空欄 \(\boxed{\ \ i \ \ }\), \(\boxed{\ \ ii \ \ }\), \(\boxed{\ \ iii \ \ }\) を埋めよ。 ただし \(G\) により生成される文字列のうち、排除したい文字列以外は、すべて \(G'\) により生成されるようにすること。 また他の数字が直後に続かない単独の 0 が現れることは許すものとする。 \(G'\) は例えば 0 や 1+301 や 0+0-203 を生成するが、00 や 1+0301 は生成しない。
Kai
【問1】
(1)
(2)
\(b\) が連続しない文字列
(3)
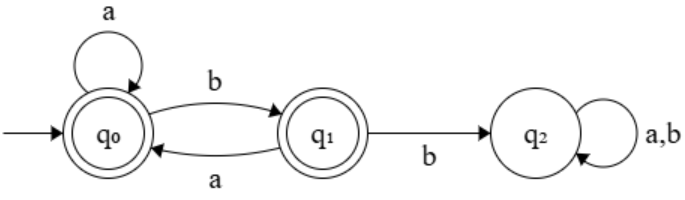
(4)
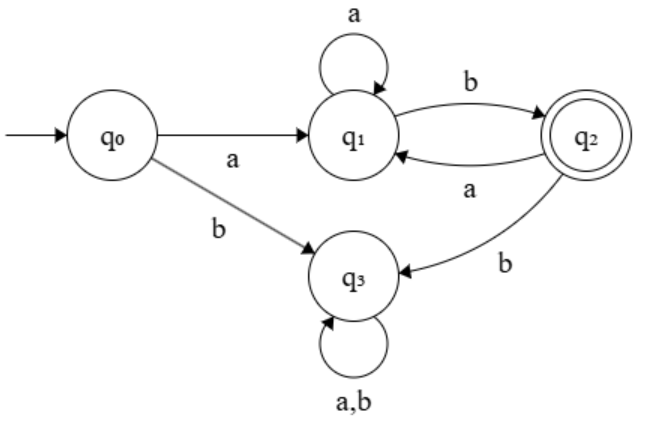
【問1】
(1)
(a)
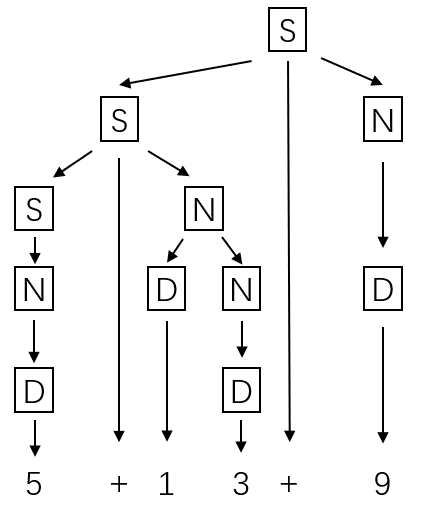
(b)
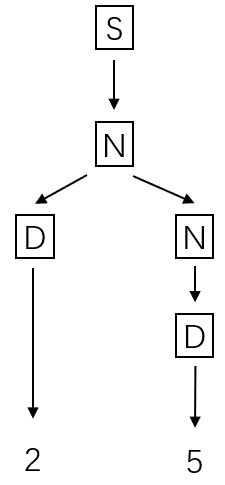
(\(c\))
生成されない。生成規則に空文字列を終端記号として導出するものが存在しない。
(d)
生成されない。文頭は最終的に非終端記号 \(S\) から導出されるが、\(S\) から「-」は導出されない。
(2)
- (i) DM
- (ii) NM
- (iii) DM
または
- (i) DM
- (ii) DM
- (iii) DM