九州大学 システム情報科学府 情報理工学専攻 2018年度 オートマトンと言語

Author

Zero

Description

【問１】

以下の遷移図を持つ非決定性有限オートマトン \(M = (K,\Sigma,\delta,q_0,F)\) に対し, 次の各問いに答えよ。ただし, \(K = \{q_0,q_1,q_2,q_3,q_4\}\), \(\Sigma = \{a,b\}\), \(\delta\), \(q_0\), \(F = \{q_1,q_2,q_4\}\) は, それぞれ状態の集合, アルファベット, 遷移関数, 初期状態, 最終状態の集合を表す。\(M\) によって受理される言語を \(L\) とする。

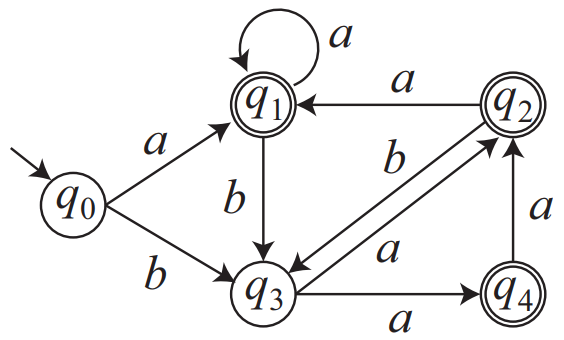
(1) \(L\) に含まれる長さ \(4\) の文字列をすべて列挙せよ。

(2) \(L\) に含まれる任意の文字列を, 正規表現 \((\alpha + \beta)(\alpha + \beta)^*\) を用いて表すことができる。ただし, \(\alpha\) と \(\beta\) はともに \(\Sigma\) 上の文字列である。これらの文字列 \(\alpha\) と \(\beta\) を与えよ。

(3) \(w\) を \(\Sigma\) 上の文字列とする。以下の \(2\) つの命題はそれぞれ真であるか偽であるか。真ならば理由を説明し, 偽ならば反例を与えよ。

• (a) 「 \(w \in L\) ならば, \(bb\) は \(w\) の部分文字列ではない。」

• (b) 「 \(bb\) が \(w\) の部分文字列でないならば, \(w \in L\) である。」

(4) \(L\) を受理する状態数最小の決定性有限オートマトンの遷移図を与えよ。

【問２】

文脈自由文法 \(G_1 = (N, \Sigma, P_1, S)\), \(G_2 = (N, \Sigma, P_2, S)\) を考える． ただし，\(N = \{S, A, B\}\), \(\Sigma = \{a, b, c\}\), \(P_i \ (i = 1, 2)\), \(S\) はそれぞれ非終端記号の集合，終端記号の集合，生成規則の集合，開始記号とする. ここで, \(P_1 = \{S \to AB, A \to ab \mid aAb, B \to c \mid Bc\}\), \(P_2 = \{S \to AB, A \to a \mid aA, B \to bBc \mid bc\}\) とする．

(1) \(G_1\) による文字列 \(aabbc\) の導出過程を与えよ．

(2) \(G_1\) が生成する言語 \(L(G_1)\) に含まれる文字列を説明せよ．

(3) \(G_2\) が生成する言語 \(L(G_2)\) に含まれる文字列を説明せよ．

(4) 言語 \(L(G_1) \cup L(G_2)\) を生成する文脈自由文法 \(G_3 = (N_3, \Sigma, P_3, S)\) の生成規則の集合 \(P_3\) を与えよ．ただし, \(N_3 = \{S, A, B, C, D\}\).

Kai

【問１】

(1)

\(b\) で終わることがない、かつ \(b\) を連続で含まないことが条件になっているので

\[ aaaa,aaba,abaa,baaa,baba \]

(2)

(1) を基に考えると

\[ \alpha = a,\beta = ba \]

(3)

(a)

真;

理由：(2) より \(\Sigma\) 上の文字列 \(w\) は, \((a + ba)(a + ba)^*\) と表せるので、\(b\) の後に連続して \(b\) がくることがないから。

(b)

偽;

反例：\(ab\)

(4)

		a	b
\(\rightarrow\)	\(q_0\)	\(q_1\)	\(q_3\)
\(*\)	\(q_1\)	\(q_1\)	\(q_3\)
\(*\)	\(q_2\)	\(q_1\)	\(q_3\)
	\(q_3\)	\(\{q_1,q_4\}\)	\(\emptyset\)
\(*\)	\(q_4\)	\(q_1\)	\(q_3\)
	\(\emptyset\)	\(\emptyset\)	\(\emptyset\)

上の表から \(q_1,q_2,\{q_1,q_4\}\) が等しいことがわかる。また、\(q_4\) はどの状態からも遷移先になっていないことが。

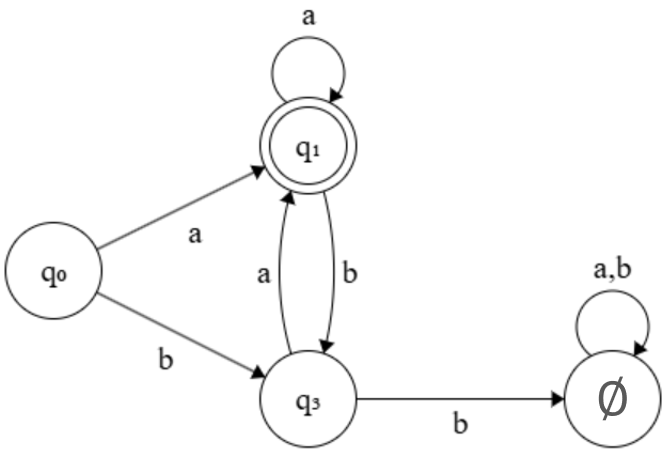
よって、遷移表は以下のようになる。

		a	b
\(\rightarrow\)	\(q_0\)	\(q_1\)	\(q_3\)
\(*\)	\(q_1\)	\(q_1\)	\(q_3\)
	\(q_3\)	\(q_1\)	\(\emptyset\)
	\(\emptyset\)	\(\emptyset\)	\(\emptyset\)

ゆえに、求める状態数最小の決定性有限オートマトン \(a\) 遷移図は

【問２】

(1)

\[ S \to AB \to aAbc \to aabbc \]

(2)

\[ L(G_1) = \{a^n b^n c^m \mid n \geq 1, m \geq 1\} \]

(3)

\[ L(G_2) = \{a^m b^n c^n \mid m \geq 1, n \geq 1\} \]

(4)

\[ \begin{aligned} P_3 = \{&S \to AB \mid CD \\ &A \to ab \mid aAb \\ &B \to c \mid Bc \\ &C \to a \mid aC \\ &D \to bDc \mid bc \} \end{aligned} \]