九州大学 システム情報科学府 情報理工学専攻 2017年度 オートマトンと言語
Author
Zero
Description
【問1】
以下の状態遷移図を持つ有限オートマトン \(M = (K, \Sigma, \delta, q_0, F)\) に対し,次の各問いに答えよ. ただし,\(K, \Sigma, \delta, q_0, F\) は,それぞれ状態の集合,アルファベット,遷移関数,初期状態,最終状態の集合を表し,\(\Sigma = \{a, b, c\}\) とする.
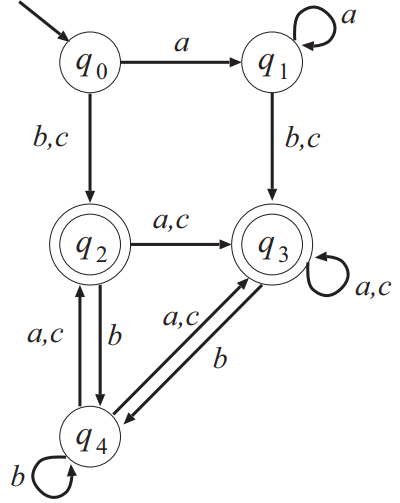
(1) \(M\) が受理する長さ \(2\) 以下の文字列をすべて列挙せよ.
(2) \(M\) が受理する言語を \(L(M)\) で表す.\(L(M)\) を受理する状態数最小の決定性有限オートマトンの状態遷移図を与えよ.
(3) \(L\) を,状態 \(q_4\) を通らずに \(M\) によって受理される文字列からなる言語とする.\(L\) を表す正規表現を1つ与えよ.
【問2】
\(\Sigma = \{a, b\}\) を終端記号の集合とする2つの文脈自由文法 \(G_1 = (N_1, \Sigma, P_1, S)\), \(G_2 = (N_2, \Sigma, P_2, T)\) を考える. ただし,\(N_1 = \{S, A\}\), \(P_1 = \{S \rightarrow aS \mid aA, A \rightarrow bA \mid b\}\), \(S\) は,それぞれ \(G_1\) の非終端記号の集合,生成規則の集合,開始記号である. また,\(N_2 = \{T, B, C\}\), \(P_2 = \{T \to aB \mid Cb, B \to \varepsilon \mid aB \mid aBb, C \to \varepsilon \mid Cb \mid aCb\}\), \(T\) は,それぞれ \(G_2\) の非終端記号の集合,生成規則の集合,開始記号である. 文脈自由文法 \(G\) が生成する言語を \(L(G)\) と表す.次の各問いに答えよ.
(1) \(G_1\) が生成する長さ 3 の文字列をすべて列挙せよ.
(2) 言語 \(L(G_1)\) を説明せよ.
(3) \(G_2\) が生成する長さ 4 の文字列をすべて列挙せよ.
(4) 言語 \(L(G_1) \setminus L(G_2)\) を説明せよ.ただし,集合 \(U, V\) について,\(U \setminus V = \{w \mid w \in U \text{ and } w \notin V\}\) とする.
Kai
【問1】
(1)
(2)
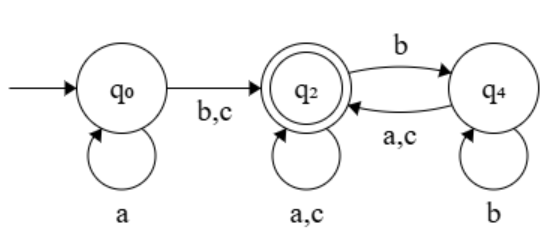
(3)
【問2】
(1)
(2)
(3)
(4)
よって、