Kyoto-University
京都大学 理学研究科 物理学・宇宙物理学専攻 2022年度 II-2C
Author Miyake
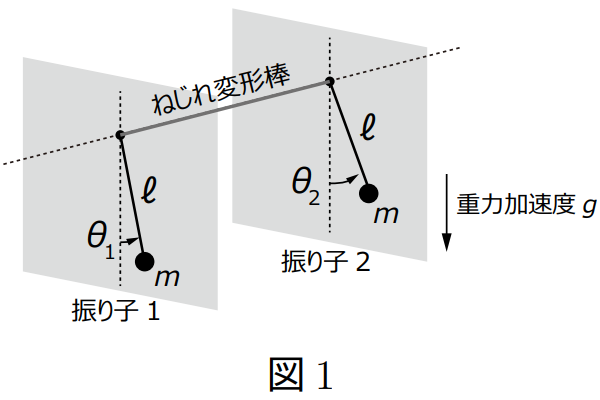
Description 図 1 のように,質量 \(m\) の質点が長さ \(l\) の太さと質量の無視できる剛体棒でつるされた振り子 \(1\) と振り子 \(2\) があり,鉛直下向き方向をむいた一様な重力(重力加速度 \(g\) )の下で運動する.
二つの振り子の支点はある水平な軸上にあり,両振り子はその軸に垂直な面内で運動する.
鉛直下向き方向と振り子の棒のなす角度を図に示すように \(\theta_1\) , \(\theta_2\) とする.
さらに,二つの振り子の支点同士はねじれ変形が可能な棒でつながれており,\(\theta_1\) と \(\theta_2\) の差に応じたエネルギー \(k(\theta_1 - \theta_2)^2/2\) (\(k\) は正の定数)が生じる.
また,以下では微小振動 \(|\theta_i| \ll 1 \ (i = 1,2)\) の場合を考え,摩擦や空気抵抗などは無視できるとする.
(1) この系の運動エネルギー \(T\) ,ポテンシャルエネルギー \(U\) ,ラグランジアン \(L = T − U\) を,\(\theta_i\) およびそれらの時間微分 \(\dot{\theta}_i\) の \(2\) 次までで求めよ.
なお,位置エネルギーに関しては,\(\theta_1 = \theta_2 = 0\) のときを基準とせよ.
(2) \(\theta_1\) および \(\theta_2\) の微小振動の微分方程式が
\[
\begin{pmatrix} \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{pmatrix}
=
\begin{pmatrix} A & B \\ C & D \end{pmatrix}
\begin{pmatrix} \theta_1 \\ \theta_2 \end{pmatrix}
\]
と書けることを示し,定数 \(A\) ,\(B\) ,\(C\) ,\(D\) を \(g\) , \(k\) , \(l\) , \(m\) を用いて表せ.
(3) \(\theta_1(t) = Q_1 \sin(\omega t + \delta_1)\) , \(\theta_2 (t) = Q_2 \sin(\omega t + \delta_2)\) (\(Q_i\) および \(\delta_i \ (i = 1,2)\) はいずれも定数)の形の解を仮定することで,この系の二つの固有角振動数 \(\omega_+\) と \(\omega_-\) (ただし \(\omega_+ > \omega_- > 0\) とする)を求め,\(g\) ,\(k\) ,\(l\) ,\(m\) を用いて表せ.
(4) それぞれの固有角振動数の解について,振幅 \(Q_i\) と位相 \(\delta_i\) の満たすべき条件を求めよ.
さらに,\(\theta_1 (t)\) と \(\theta_2 (t)\) の一般解を,\(\omega_+\) と \(\omega_-\) および適切に導入した任意定数を用いて表せ.
(5) 振り子 \(1\) と \(2\) が共に \(\theta_1 = \theta_2 = 0\) で静止している状態から,時刻 \(t = 0\) で振り子 \(1\) に角速度 \(\Omega_0 \ (0 < \Omega_0 \ll \omega_-)\) を与えた.
この場合の \(t > 0\) での \(\theta_1\) と \(\theta_2\) の時間依存性を,\(\omega_+\) , \(\omega_-\) , \(\Omega_0\) を用いて表せ.
さらに,\(\omega_+\) と \(\omega_-\) の大きさが近い場合の \(\theta_1\) と \(\theta_2\) の時間依存性の特徴を簡潔に述べよ.
Kai (1)
\[
\begin{aligned}
T
&= \frac{1}{2} m l^2 \dot{\theta}_1^2 + \frac{1}{2} m l^2 \dot{\theta}_2^2
\\
U
&= mgl (1 - \cos \theta_1) + mgl (1 - \cos \theta_2)
+ \frac{1}{2} k (\theta_1 - \theta_2)^2
\\
&\simeq \frac{1}{2} mgl \theta_1^2 + \frac{1}{2} mgl \theta_2^2
+ \frac{1}{2} k (\theta_1 - \theta_2)^2
\\
&= \frac{1}{2} (mgl+k) \left( \theta_1^2 + \theta_2^2 \right)
- k \theta_1 \theta_2
\\
L
&= T - U
\\
&=
\frac{1}{2} m l^2 \dot{\theta}_1^2 + \frac{1}{2} m l^2 \dot{\theta}_2^2
- \frac{1}{2} (mgl+k) \left( \theta_1^2 + \theta_2^2 \right)
+ k \theta_1 \theta_2
\end{aligned}
\]
(2)
\[
\begin{aligned}
\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}_1}
&= \frac{d}{dt} ml^2 \dot{\theta}_1
= ml^2 \ddot{\theta}_1
\\
\frac{\partial L}{\partial \theta_1}
&= -(mgl+k) \theta_1 + k \theta_2
\\
\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}_2}
&= \frac{d}{dt} ml^2 \dot{\theta}_2
= ml^2 \ddot{\theta}_2
\\
\frac{\partial L}{\partial \theta_2}
&= -(mgl+k) \theta_2 + k \theta_1
\end{aligned}
\]
であるから、\(\theta_1, \theta_2\) に関するオイラー-ラグランジュの方程式より、
\[
\begin{aligned}
ml^2 \begin{pmatrix} \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{pmatrix}
=
\begin{pmatrix} -(mgl+k) & k \\ k & -(mgl+k) \end{pmatrix}
\begin{pmatrix} \theta_1 \\ \theta_2 \end{pmatrix}
\end{aligned}
\]
であり、
\[
\begin{aligned}
A = - \frac{mgl+k}{ml^2}
, \ \
B = \frac{k}{ml^2}
, \ \
C = \frac{k}{ml^2}
, \ \
D = - \frac{mgl+k}{ml^2}
\end{aligned}
\]
がわかる。
(3)
(2) で得た運動方程式に
\(\theta_1(t)=Q_1 \sin (\omega t + \delta_1), \ \theta_2(t)=Q_2 \sin (\omega t + \delta_2)\)
を代入すると、
\[
\begin{aligned}
- \omega^2
\begin{pmatrix}
Q_1 \sin (\omega t + \delta_1) \\
Q_2 \sin (\omega t + \delta_2) \\
\end{pmatrix}
=
\begin{pmatrix} A & B \\ B & A \end{pmatrix}
\begin{pmatrix}
Q_1 \sin (\omega t + \delta_1) \\
Q_2 \sin (\omega t + \delta_2) \\
\end{pmatrix}
\end{aligned}
\]
となる。
\(Q_1=Q_2=0\) 以外で、任意の \(t\) についてこれが成り立つためには、
以下が必要である:
\[
\begin{aligned}
0
&= \det
\begin{pmatrix} \omega^2 + A & B \\ B & \omega^2 + A \end{pmatrix}
\\
&= \omega^4 + 2A \omega^2 + A^2 - B^2
\\
&= \left( \omega^2 + (A+B) \right) \left( \omega^2 + (A-B) \right)
\end{aligned}
\]
\(0 \lt -A-B \lt -A+B\) なので、
\[
\begin{aligned}
\omega_- &= \sqrt{-A-B} = \sqrt{\frac{g}{l}}
\\
\omega_+ &= \sqrt{-A+B} = \sqrt{\frac{mgl+2k}{ml^2}}
\end{aligned}
\]
を得る。
(4)
(i)
\(\omega = \omega_-\) の場合を考える。
\[
\begin{aligned}
\begin{pmatrix} A & B \\ B & A \end{pmatrix}
\begin{pmatrix} u \\ v \end{pmatrix}
=
(A+B)
\begin{pmatrix} u \\ v \end{pmatrix}
\end{aligned}
\]
とおくと \(u=v\) を得るから、
\(Q_1 \sin (\omega_- t + \delta_1) = Q_2 \sin (\omega_- t + \delta_2)\)
であり、任意の \(t\) についてこれが成り立つということは
\(Q_1 = Q_2, \ \delta_1 = \delta_2\) ということであり、
これが求める条件である。
(ii)
\(\omega = \omega_+\) の場合を考える。
\[
\begin{aligned}
\begin{pmatrix} A & B \\ B & A \end{pmatrix}
\begin{pmatrix} u \\ v \end{pmatrix}
=
(A-B)
\begin{pmatrix} u \\ v \end{pmatrix}
\end{aligned}
\]
とおくと \(u+v=0\) を得るから、
\(Q_1 \sin (\omega_- t + \delta_1) = -Q_2 \sin (\omega_- t + \delta_2)\)
であり、任意の \(t\) についてこれが成り立つということは
\(Q_1 = -Q_2, \ \delta_1 = \delta_2\)
(あるいは \(Q_1 = Q_2, \ |\delta_1 - \delta_2| = \pi\) )
ということであり、これが求める条件である。
(i), (ii) より、求める一般解は、
\(Q_-, \delta_-, Q_+, \delta_+\) を任意定数として、
\[
\begin{aligned}
\theta_1(t)
&= Q_- \sin (\omega_- t + \delta_-) + Q_+ \sin (\omega_+ t + \delta_+)
\\
\theta_2(t)
&= Q_- \sin (\omega_- t + \delta_-) - Q_+ \sin (\omega_+ t + \delta_+)
\end{aligned}
\]
である。
これが (2) で求めた運動方程式を満たすことを確認できる。
(5)
初期条件
\[
\begin{aligned}
0 &= \theta_1(0) = Q_- \sin \delta_- + Q_+ \sin \delta_+
\\
0 &= \theta_2(0) = Q_- \sin \delta_- - Q_+ \sin \delta_+
\\
\Omega_0 &= \dot{\theta}_1(0)
= Q_- \omega_- \cos \delta_- + Q_+ \omega_+ \cos \delta_+
\\
0 &= \dot{\theta}_2(0)
= Q_- \omega_- \cos \delta_- - Q_+ \omega_+ \cos \delta_+
\end{aligned}
\]
から、
\[
\begin{aligned}
\delta_- = \delta_+ = 0
, \ \
Q_- = \frac{\Omega_0}{2 \omega_-}
, \ \
Q_+ = \frac{\Omega_0}{2 \omega_+}
\end{aligned}
\]
がわかるので、
\[
\begin{aligned}
\theta_1(t)
&= \frac{\Omega_0}{2 \omega_-} \sin (\omega_- t)
+ \frac{\Omega_0}{2 \omega_+} \sin (\omega_+ t)
\\
\theta_2(t)
&= \frac{\Omega_0}{2 \omega_-} \sin (\omega_- t)
- \frac{\Omega_0}{2 \omega_+} \sin (\omega_+ t)
\end{aligned}
\]
を得る。