神戸大学 システム情報学研究科 2017年8月実施 専門科目 システム理論 [1]

Author

祭音Myyura

Description

\(A\) ~ \(E\) の各地点の間に光ファイバーを設置してインターネットで相互につながるようにしたい。 ただし、2つの地点の間で直接つながるか、他地点を経由してつながるかは問わないとする。 図 (a) に示されたグラフは、各点 (vertex) が地点 \(A\) ~ \(B\) のいずれかに対応し、各辺 (edge) がその両端に対応する 2 地点間に光ファイバーが設置可能であることを示す (辺のない 2 地点間は地理的な条件などにより光ファイバーが設置できないことを示す)。

以下の設問に答えよ。

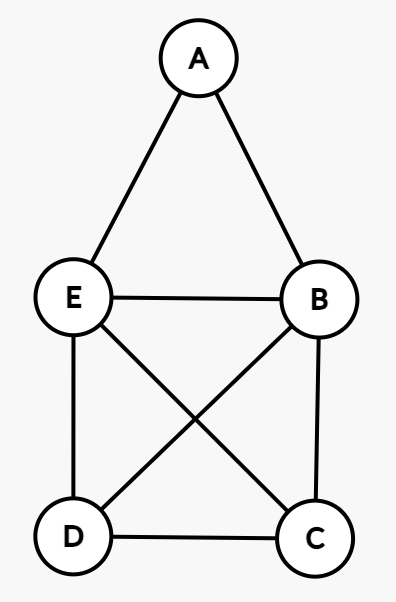
図 (a)

(1) 図 (a) に示されたグラフについて、隣接行列 (adjacency matrix) およびラプラシアン行列 (Laplacian matrix) を示せ。

(2) 図 (a) に示されたグラフの全域木 (spanning tree) は、\(A\) ~ \(E\) の各々を一度だけ通り、かつ、閉路 (cycle) のないような連結した光ファイバー網に対応する。このとき、全域木の辺の数はいくつか示せ。また、全域木が何通りあるか示せ。ただし、根拠も示せ。

(3) 表 (b) は、光ファイバーが設置可能な 2 地点間についてそれぞれの設置費用を 1000 万円を単位として示したものである。前問 (2) の全域木のうち、光ファイバーの設置に係る総費用が最小となる場合について、その総費用を示せ。

	A	B	C	D	E
A	-	1	-	-	4
B		-	2	7	3
C			-	8	5
D				-	6
E					-

表 (b)

Kai

(1)

隣接行列 \(\boldsymbol{A}\)

\[ \boldsymbol{A} = \begin{pmatrix} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{pmatrix} \]

次数行列 \(\boldsymbol{D}\)

\[ \boldsymbol{D} = \begin{pmatrix} 2 & 0 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 4 \end{pmatrix} \]

ラプラシアン行列 \(\boldsymbol{L}\)

\[ \boldsymbol{L} = \boldsymbol{D} - \boldsymbol{A} = \begin{pmatrix} 2 & -1 & 0 & 0 & -1 \\ -1 & 4 & -1 & -1 & -1 \\ 0 & -1 & 3 & -1 & -1 \\ 0 & -1 & -1 & 3 & -1 \\ -1 & -1 & -1 & -1 & 4 \end{pmatrix} \]

(2)

行列木定理より、\(\boldsymbol{L}\) の \(11\) 余因子 \(\Delta_{11}\) は

\[ \Delta_{11} = \text{det} \begin{pmatrix} 4 & -1 & -1 & -1 \\ -1 & 3 & -1 & -1 \\ -1 & -1 & 3 & -1 \\ -1 & -1 & -1 & 4 \end{pmatrix} = 40 \]

であるので、図 (a) に示されたグラフの全域木の個数も 40 である。

(3)

最小木

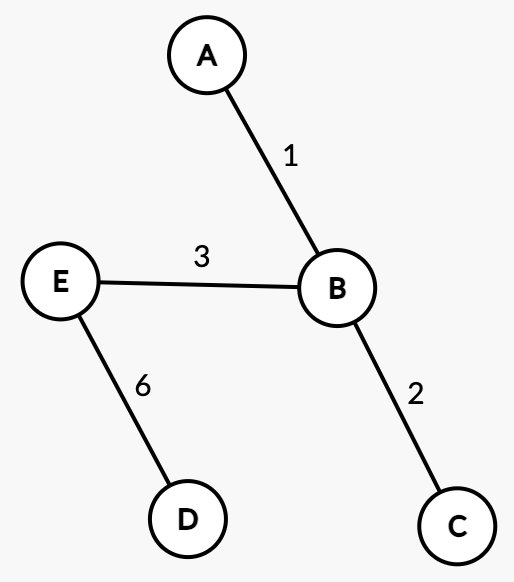
最小総費用は 12 である。