神戸大学システム情報学研究科 2017年8月実施専門科目計算機科学 [2]

Author

祭音Myyura

Description

グラフ (graph) の探索 (search) においては、同一ノード (頂点，node, vertex) を何度も探索しないように注意が必要である。下図 (a) は、有向グラフ (directed graph) を対象に探索をおこなう C 言語のプログラムの例である。 struct node はグラフのノードを表す。フィールド s，t がノードへの参照を値として持つことは、そのノードから参照先ノードへのエッジ (edge) が存在することを示す (NULL 値の場合は対応エッジはない)。 id はノードの識別子であり、visited はノードの訪問回数を示す。関数　dfs(node) は、node を起点にエッジにそってグラフの探索をおこなう再帰関数である。

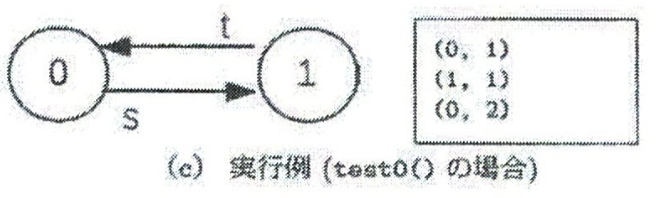
(b) の test0, 1, 2, 3 関数は、グラフを生成した上で、 dfs 関数を実行するテストプログラム群である。例として、test0 関数が生成するグラフ (ノード: 0,1) と、関数を実行した際の標準出力結果を (\(c\)) 実行例に示す。図の (s, t) は、それぞれのエッジが、エッジの起点ノードから s もしくは t の参照先ノードへのエッジであることを示す。

以下の各間に答えよ、回答順は出題と異なっても構わない、また、標準出力結果中の改行については、追加・削除していても構わないものとする。

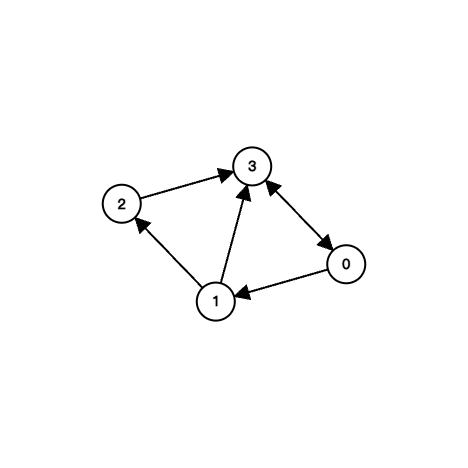
(1) test1 関数が生成するグラフ（ノード：0 ~ 3）と、関数を実行した際の標準出力結果を、(\(c\)) にならって示せ。

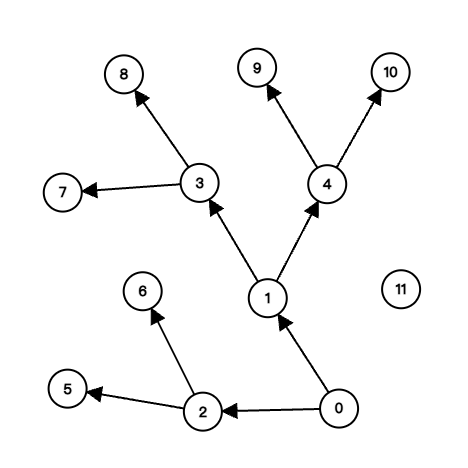
(2) test2 関数が生成するグラフ（ノード：0 ~ 11）と、関数を実行した際の標準出力結果を、(\(c\)) にならって示せ。

(3) test3 関数が生成するグラフ（ノード：0 ~ 11）を示せ。加えて、仮に (a) 18 行目 (if 文) を完全に取り除いた場合に、test3 関数を実行した際の nodes[10] の訪問回数が最終的に何回になるか、簡単な理由とともに答えよ。

#include <stdio.h>
#define BUFSIZE 20
typedef struct node {
    struct node *s;
    struct node *t;
    int id; int visited;
} *node_tp;
struct node nodes[BUFSIZE];

void printNode(node_tp node) {
    printf("(%d, %d)\n", node->id, node->visited);
}
void dfs(node_tp node) {
    node_tp s = node->s;
    node_tp t = node->t;
    node->visited++;
    printNode(node);
    if (node->visited > 1) return;
    if (s != NULL) dfs(s);
    if (t != NULL) dfs(t);
}
void initNodes(int n) {
    int i;
    for (i = 0; i < n; i++) {
        nodes[i].id = i; nodes[i].visited = 0;
        nodes[i].s = nodes[i].t = NULL;
    }
}
void link(node_tp node, node_tp s, node_tp t) {
    node->s = s; node->t = t;
}

(a) プログラム (主要部)

void test0(void) {
    initNodes(2);
    link(&nodes[0], &nodes[1], NULL);
    link(&nodes[1], NULL, &nodes[0]);
    dfs(&nodes[0]); /* ノード 0 から探索 */ 
}

void test1(void) {
    initNodes(4);
    link(&nodes[0], &nodes[3], &nodes[1]);
    link(&nodes[1], &nodes[3], &nodes[2]);
    link(&nodes[2], &nodes[3], NULL);
    link(&nodes[3], NULL, &nodes[0]);
    dfs(&nodes[1]); /* ノード 1 から探索 */ 
}

void test2(void) {
    int i;
    initNodes(12);
    for (i = 0; i < 5; i++) {
        link(&nodes[i], &nodes[2*i+1], &nodes[2*i+2]);
    }
    dfs(&nodes[1]); /* ノード 1 から探索 */ 
    printf("---\n");
    dfs(&nodes[0]); /* ノード 0 から探索 */ 
}

void test3(void) {
    int i;
    initNodes(12);
    for (i = 0; i < 10; i++) {
        link(&nodes[i], &nodes[i+1], &nodes[i+2]);
    }
    dfs(&nodes[0]); /* ノード 0 から探索 */ 
}

(b) テストプログラム群

Kai

(1)

(1, 1)
(3, 1)
(0, 1)
(3, 2)
(1, 2)
(2, 1)
(3, 3)

(2)

(1, 1)
(3, 1)
(7, 1)
(8, 1)
(4, 1)
(9, 1)
(10, 1)
---
(0, 1)
(1, 2)
(2, 1)
(5, 1)
(6, 1)

(3)

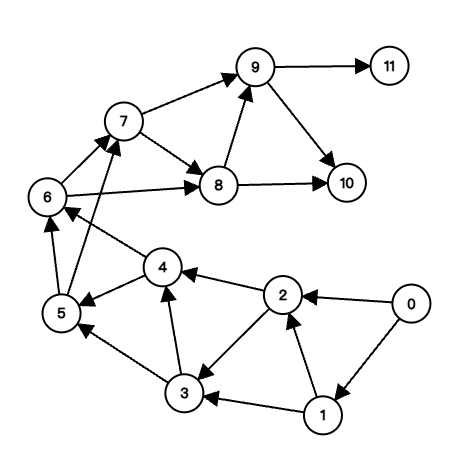
\(F(n)\) をノード \(n\) から探索する場合、nodes[10] の訪問回数と定める。このとき、

\[ \begin{aligned} F(9) &= 1 \\ F(8) &= 1 + F(9) \\ F(7) &= F(8) + F(9) \\ F(6) &= F(7) + F(8) \\ &\cdots \\ F(0) &= F(1) + F(2) \end{aligned} \]

と計算できるので、

\[ F(0) = 89 \]

である。

神戸大学 システム情報学研究科 2017年8月実施 専門科目 計算機科学 [2]