Hiroshima-University
広島大学 先進理工系科学研究科 物理学プログラム 2022年8月実施 専門科目 [4] 熱統計力学
Author Miyake
Description 以下の問いに答えよ.
(1) エンタルピー \(H\) は内部エネルギー \(U\) 、圧力 \(p\) 、体積 \(V\) を用いて、\(H = U + pV\) と表わされる。
この式と熱力学第 1 法則および比熱の定義式から、定圧比熱 \(C_p\) 、エンタルピー、温度 \(T\) 、圧力 \(p\) の間に \(C_p = \left( \frac{\partial H}{\partial T} \right)_p\) が成り立つことを示せ。
(2) ある閉じた系の内部エネルギーの微小変化 \(dU\) は、エントロピー \(S\) と体積 \(V\) の微小変化 \(dS, dV\) を用いて、\(dU = TdS - pdV\) と表される。
この関係式を用いて、エントロピー \(S\) とエンタルピー \(H\) の間に、下記の2つの関係式が成り立つことを示せ。
\[
\left( \frac{\partial S}{\partial T} \right)_p = \frac{1}{T} \left( \frac{\partial H}{\partial T} \right)_p
\]
\[
\left( \frac{\partial S}{\partial p} \right)_T = \frac{1}{T} \left( \frac{\partial H}{\partial p} \right)_T - \frac{V}{T}
\]
(3) 問(2)の関係式を用いて、下記の関係式が成り立つことを示せ。
\[
\left( \frac{\partial H}{\partial p} \right)_T = -T \left( \frac{\partial V}{\partial T} \right)_p + V
\]
(4) エンタルピーが保存される場合について、\(\left( \frac{\partial H}{\partial p} \right)_T\) を \(T, V, C_p\) , \(\left( \frac{\partial V}{\partial T} \right)_p\) で表せ。
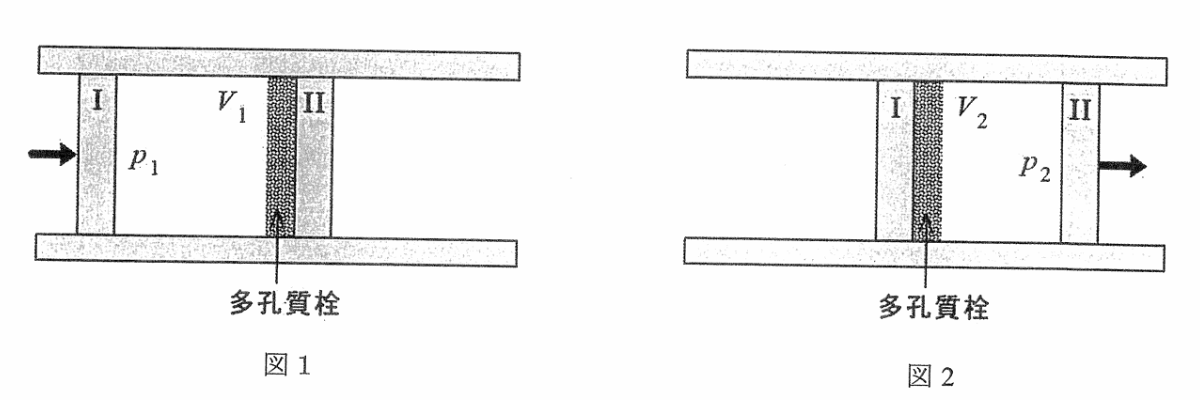
下図のように、断熱壁で作られたシリンダーの中央部に綿などでできた多孔質栓を固定して、断熱材で作られたピストン I, II を用いて左側から右側にゆっくり気体を押し出したとき、押し出される前と後の気体の温度がどのように変化するかを調べる実験を考える。
最初に図 1 のように、ピストン I で多孔質栓より左側に体積 \(V_1\) の気体を閉じ込め、ピストン II は多孔質栓の右側に密着している。
この状態から、ピストン I, II にかかる圧力 \(p_1, p_2\ (p_1 > p_2)\) を一定に保ちながらゆっくりそれぞれのピストンを動かし、最終的に図 2 のように、ピストン I を多孔質栓に密着するまで動かしたとする。
その時、多孔質栓の右側部分に押し出された気体の体積は \(V_2\) となった。
この過程について、以下の問いに答えよ。ただし、多孔質栓の体積は無視できるとする。
(5) この過程でエンタルピーが保存されることを示せ。
(6) 問(4)の結果を用いて、気体が理想気体の場合、押し出される前後で気体の温度は変化しないことを示せ。
Kai (1)
微小な熱 \(d'Q\) を受け取ったときの \(U,H,p,V,T\) の変化量を \(dU,dH,dp,dV,dT\)
とすると、熱力学第1法則より
\[
\begin{aligned}
dU = d'Q - pdV
\end{aligned}
\]
が成り立ち、 \(H=U+pV\) より
\[
\begin{aligned}
dH &= dU + pdV + Vdp
\\
&= d'Q + Vdp
\end{aligned}
\]
が成り立つ。
定圧変化では \(dp=0\) であるから \(dH=d'Q\) となり、
\[
\begin{aligned}
C_p
&= \left( \frac{\partial H}{\partial T} \right)_p
\end{aligned}
\]
がわかる。
(2)
\(dU=TdS-pdV\) から
\[
\begin{aligned}
dH &= TdS+Vdp
\\
\therefore \ \
dS &= \frac{1}{T} dH - \frac{V}{T} dp
\end{aligned}
\]
がわかるので、
\[
\begin{aligned}
\left( \frac{\partial S}{\partial T} \right)_p
&= \frac{1}{T} \left( \frac{\partial H}{\partial T} \right)_p
,
\\
\left( \frac{\partial S}{\partial p} \right)_T
&= \frac{1}{T} \left( \frac{\partial H}{\partial p} \right)_T - \frac{V}{T}
\end{aligned}
\]
がわかる。
(3)
\(G=H-TS\) とおくと、
\[
\begin{aligned}
dG = -SdT + Vdp
\end{aligned}
\]
であり、 (2) で得た式を使って、次のように計算できる:
\[
\begin{aligned}
\left( \frac{\partial H}{\partial p} \right)_T
&= T \left( \frac{\partial S}{\partial p} \right)_T + V
\\
&= - T \frac{\partial^2 G}{\partial p \partial T} + V
\\
&= - T \frac{\partial^2 G}{\partial T \partial p} + V
\\
&= - T \left( \frac{\partial V}{\partial T} \right)_p + V
\end{aligned}
\]
(4)
\[
\begin{aligned}
\left( \frac{\partial T}{\partial p} \right)_H
&= - \frac{\left( \frac{\partial H}{\partial p} \right)_T}
{\left( \frac{\partial H}{\partial T} \right)_p}
\ \ \ \ \ \ \ \ (\because \text{偏微分の公式})
\\
&= - \frac{1}{C_p} \left( - T \left( \frac{\partial V}{\partial T} \right)_p + V \right)
\ \ \ \ \ \ \ \ (\because \text{(1), (3)})
\\
&= \frac{1}{C_p} \left( T \left( \frac{\partial V}{\partial T} \right)_p - V \right)
\end{aligned}
\]
(5)
図 1 の状態での内部エネルギーを \(U_1\) 、エンタルピーを \(H_1\) とし、
図 2 の状態での内部エネルギーを \(U_2\) 、エンタルピーを \(H_2\) とすると、次が成り立つ:
\[
\begin{aligned}
H_1 &= U_1 + p_1V_1
\\
H_2 &= U_2 + p_2V_2
\end{aligned}
\]
左側のピストンが気体になす仕事は \(p_1V_1\) であり、
右側のピストンが気体になす仕事は \(-p_2V_2\) であり、
熱の出入りはないから、熱力学第1法則より次が成り立つ:
\[
\begin{aligned}
U_2 - U_1 = p_1V_1 - p_2V_2
\end{aligned}
\]
よって、 \(H_1=H_2\) が成り立ち、エンタルピーが保存されることがわかる。
(6)
理想気体の状態方程式は適当な定数 \(c\) を使って \(pV=cT\) と書けるので、
\[
\begin{aligned}
T \left( \frac{\partial V}{\partial T} \right)_p - V
&= T \cdot \frac{c}{p} - \frac{cT}{p}
\\
&= 0
\end{aligned}
\]
が成り立ち、したがって (4) から
\[
\begin{aligned}
\left( \frac{\partial T}{\partial p} \right)_H &= 0
\end{aligned}
\]
が成り立ち、気体の温度が変化しないことがわかる。