広島大学 先進理工系科学研究科 物理学プログラム 2022年8月実施 専門科目 [1] 力学
Author
Miyake
Description
1.
ばね定数 \(k\) のばねが、滑らかで水平な床に置かれ、片側は壁に固定されており、もう片方に質量 \(m\) の質点が取り付けられている。
空気から質点には速度に比例した抵抗が働くものとし、その比例係数を \(c\) とする。
ばねは平行に座標 \(x\) を取り、ばねが自然長の時の質点の位置を原点とし、壁と逆側の向きを正の方向とする。壁に垂直な方向の質点の運動のみ考えることとして、以下の問いに答えよ。
(1) この系の運動方程式を立てよ。
(2) \(c^2 < 4mk\) のとき、運動方程式の一般解を求め、どのような運動をするのか図を用いて説明せよ。
(2) \(c^2 > 4mk\) のとき、運動方程式の一般解を求め、どのような運動をするのか図を用いて説明せよ。
2.
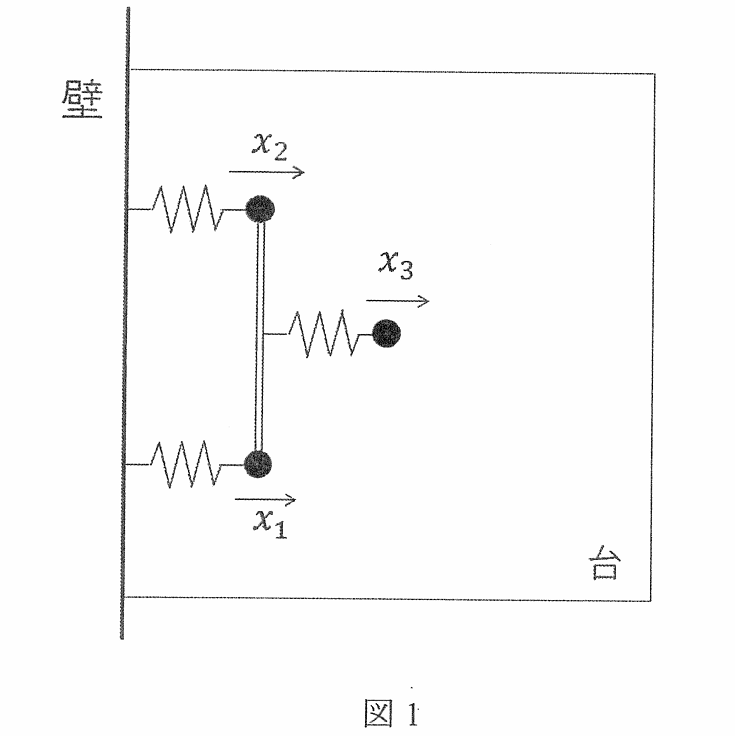
図 1 のように3つの質点と3つのばねと1つの棒が組み合わされて構成され、壁に取り付けられて水平な台に置かれた系を考える。
すべての質点の質量を \(m\)、すべてのばねのばね定数を \(k\) とする。
また、棒の長さを \(2a\) とし、1つのばねは棒の中点の場所に取り付けられているものとする。
棒は伸び縮みせず、たわまないものとし、棒の質量は無視できるものとする。
台の表面は滑らかであるとする。
それぞれの質点の座標を \(x_1, x_2, x_3\) とし、ばねが自然長の時の質点の位置を原点とし、壁と逆側の向きを正の方向とする。
この系の質点の振動モードについて以下の問いに答えよ。
ただし、質点の振動の振幅は小さいものとし、壁に垂直な運動のみ考えるものとし、壁に平行な方向の運動は微小なものとして無視する。
空気からの抵抗も考えない(\(c = 0\))ものとする。
(1) この系のラグランジアンを求めよ。
(2) 上で求めたラグランジアンより、この系の運動方程式を導出せよ。
(3) この系の固有振動モードの1つは、棒の中点が静止した状態で、棒の両端が逆位相で振動するものである。
棒の中点の周りに関する回転の運動方程式を導出し、その角振動数が \(\omega_1 = \sqrt{\frac{k}{m}}\) であることを示せ。
上の (2) で求めた式を利用しても良い。
(4) この系の固有角振動数について、\(\omega_1\) 以外の2つを求めよ。
(5) この系の固有振動モードは3種類ある。それぞれを図を用いて説明せよ。
Kai
時刻を \(t\) で表し、時間微分を \(d/dt\) や \(\dot{}\) で表す。
1.
(1)
\[
\begin{aligned}
m \ddot{x} = - kx - c \dot{x}
\end{aligned}
\]
(2)
(1) の運動方程式に \(x = e^{\lambda t}\) ( \(\lambda\) は \(t\) によらない定数)を代入すると、
\[
\begin{aligned}
m \lambda^2 + c \lambda + k = 0
\end{aligned}
\]
\[
\begin{aligned}
\therefore \ \
\lambda
&= \frac{-c \pm \sqrt{c^2 - 4mk}}{2m}
\\
&= \frac{-c \pm i \sqrt{4mk - c^2}}{2m}
\end{aligned}
\]
を得る。よって、 \(c^2 \lt 4mk\) のときの一般解は、任意定数を \(A,B\) として、
\[
\begin{aligned}
x(t)
&= \left(
A \sin \left( \frac{\sqrt{4mk - c^2}}{2m} t \right)
+ B \sin \left( \frac{\sqrt{4mk - c^2}}{2m} t \right)
\right) \exp \left( - \frac{c}{2m} t \right)
\end{aligned}
\]
である。
(3)
\(c^2 \gt 4mk\) のときの一般解は、任意定数を \(A,B\) として、
\[
\begin{aligned}
x(t)
&= A \exp \left( \frac{-c + \sqrt{c^2 - 4mk}}{2m} t \right)
+ B \exp \left( \frac{-c - \sqrt{c^2 - 4mk}}{2m} t \right)
\end{aligned}
\]
である。
2.
(1)
求めるラグランジアン \(L\) は、
\[
\begin{aligned}
L
&= \frac{1}{2} m \left( \dot{x}_1^2 + \dot{x}_2^2 + \dot{x}_3^2 \right)
- \frac{1}{2} k
\left( x_1^2 + x_2^2 + \left( x_3 - \frac{x_1+x_2}{2} \right)^2 \right)
\end{aligned}
\]
(2)
\[
\begin{aligned}
\frac{d}{dt} \frac{\partial L}{\partial \dot{x}_1}
&= \frac{d}{dt} m \dot{x}_1 = m \ddot{x}_1
\\
\frac{d}{dt} \frac{\partial L}{\partial \dot{x}_2}
&= \frac{d}{dt} m \dot{x}_2 = m \ddot{x}_2
\\
\frac{d}{dt} \frac{\partial L}{\partial \dot{x}_3}
&= \frac{d}{dt} m \dot{x}_3 = m \ddot{x}_3
\\
\frac{\partial L}{\partial x_1}
&= - k x_1 + \frac{1}{2} k \left( x_3 - \frac{x_1+x_2}{2} \right)
\\
&= - \frac{1}{4} k \left( 5 x_1 + x_2 - 2 x_3 \right)
\\
\frac{\partial L}{\partial x_2}
&= - k x_2 + \frac{1}{2} k \left( x_3 - \frac{x_1+x_2}{2} \right)
\\
&= - \frac{1}{4} k \left( x_1 + 5 x_2 - 2 x_3 \right)
\\
\frac{\partial L}{\partial x_3}
&= - k \left( x_3 - \frac{x_1+x_2}{2} \right)
\\
&= - \frac{1}{2} k \left( - x_1 - x_2 + 2 x_3 \right)
\end{aligned}
\]
より、
\[
\begin{aligned}
m \ddot{x}_1 &= - \frac{1}{4} k \left( 5 x_1 + x_2 - 2 x_3 \right)
\\
m \ddot{x}_2 &= - \frac{1}{4} k \left( x_1 + 5 x_2 - 2 x_3 \right)
\\
m \ddot{x}_3 &= - \frac{1}{2} k \left( - x_1 - x_2 + 2 x_3 \right)
\end{aligned}
\]
(3)
(2) で求めた運動方程式は、次のように書ける:
\[
\begin{aligned}
\frac{d^2}{dt^2} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}
=
- \frac{\omega_1^2}{4}
\begin{pmatrix} 5 & 1 & -2 \\ 1 & 5 & -2 \\ -2 & -2 & 4 \end{pmatrix}
\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}
\end{aligned}
\]
\(x_1 = \xi, x_2 = - \xi, x_3 = 0\) の場合を考えると、
\[
\begin{aligned}
\begin{pmatrix} 5 & 1 & -2 \\ 1 & 5 & -2 \\ -2 & -2 & 4 \end{pmatrix}
\begin{pmatrix} \xi \\ - \xi \\ 0 \end{pmatrix}
= 4 \begin{pmatrix} \xi \\ - \xi \\ 0 \end{pmatrix}
\end{aligned}
\]
となるので、これは角振動数 \(\omega_1\) の固有振動モードであることがわかる。
(4)
(3) で現れた行列
\[
\begin{aligned}
\Lambda
= \begin{pmatrix} 5 & 1 & -2 \\ 1 & 5 & -2 \\ -2 & -2 & 4 \end{pmatrix}
\end{aligned}
\]
の固有値を \(\lambda\) とすると、
\[
\begin{aligned}
0
&= \det \begin{pmatrix}
5 - \lambda & 1 & -2 \\ 1 & 5 - \lambda & -2 \\ -2 & -2 & 4 - \lambda
\end{pmatrix}
\\
&= - (\lambda-2)(\lambda-4)(\lambda-8)
\\
\therefore \ \
\lambda &= 2, 4, 8
\end{aligned}
\]
なので、\(\omega_1\) 以外の固有角振動数は \(\omega_1 / \sqrt{2}, 2 \omega_1\) である。
(5)
(4) の行列 \(\Lambda\) の固有値 \(2, 4, 8\) に属する固有ベクトルはそれぞれ
\[
\begin{aligned}
\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}
, \ \
\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}
, \ \
\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}
\end{aligned}
\]
であるので、固有角振動数 \(\omega_1 / \sqrt{2}, \omega_1, 2 \omega_1\) の固有振動モードはそれぞれ
\[
\begin{aligned}
\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}
&=
A \sin \left( \frac{\omega_1}{\sqrt{2}} t + \alpha \right)
\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}
,
B \sin \left( \omega_1 t + \beta \right)
\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}
,
C \sin \left( 2 \omega_1 t + \gamma \right)
\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}
\end{aligned}
\]
と書ける。( \(A,B,C,\alpha,\beta,\gamma\) は初期条件から決まる定数である。)
